「CODVES 1922 」骑士共存问题（二分图的最大独立集|网络流）&dinic
首先是题目链接 http://codevs.cn/problem/1922/
结果发现题目没图（心情复杂
然后去网上扒了一张图
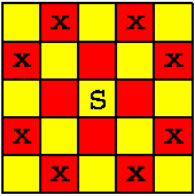
大概就是这样了。
如果把每个点和它可以攻击的点连一条边，那问题就变成了求二分图的最大独立集了 （二分图最大独立集：即一个点集，集合中任两个结点不相邻），然后就是建图了。
题图非常好心的帮忙染色了，所以我们可以看出来，一个点可以到达的点和它的颜色是不一样的，所以只需要黑白染色就可以了，然后把黑点看作一个集合， 白点看作一个集合，又因为二分图最大独立集=顶点总数 - 最大匹配，而后我们就只需要求最大匹配就可以了。
最大匹配最经典的就是匈牙利啦，但是网络流也可以做， 而且dinic在边容量为一的时候跑得特别快，所以就用dinic了（顺便练习一下dinic233
建图方法：超级源S连接所有的黑点，且边的容量为1, 黑点连接它所有能攻击到的白点，边的容量为INF， 然后所有的白点再连接超级汇T， 容量仍然是为1。跑一遍dinic就可以了（建图的正确性可以自己画图证明
#include <cstdio>
#include <vector>
#include <cstring>
#include <algorithm>
#include <queue>
#include <iostream>
using namespace std;
const int N = ; int n, m, cnt, w; struct Edge{
int from, to, cap, flow;
};
vector < int > G[N*N];
vector < Edge > edge;
bool vis[N*N];
int s, t, d[N*N], cur[N*N], INF = (<<), flag[N][N];
int py[][] = {{, }, {, -}, {-, }, {-, -}, {, }, {, -}, {-, }, {-, -}}; inline void read(int &ans){
static char buf = getchar();
register int neg = ;
ans = ;
for (;!isdigit(buf); buf = getchar())
if (buf == '-') neg = -;
for (;isdigit(buf); buf = getchar())
ans = ans* + buf - '';
ans *= neg;
} inline void Add(int from, int to, int cap){
edge.push_back((Edge){from, to, cap, });
edge.push_back((Edge){to, from, , });
int m = edge.size();
G[from].push_back(m - );
G[to].push_back(m - );
} bool ok(int x, int y){
if (x > && x <= n && y > && y <= n)
if (flag[x][y] != -)
return true;
return false;
} inline void build(){
for (int i = ; i <= n; i++)
for (int j = ; j <= n; j++)
if (flag[i][j] == -) continue;
else if (flag[i][j] < cnt){
for (int k = ; k < ; k++){
int x = i + py[k][];
int y = j + py[k][];
if (ok(x, y))
Add(flag[i][j], flag[x][y], INF);
}
Add(, flag[i][j], );
}
else Add(flag[i][j], w, );
} inline bool BFS(){
memset(vis, , sizeof(vis));
memset(d, 0xff, sizeof(d));
queue < int > q;
q.push(s);
d[s] = ;
vis[s] = ;
while(!q.empty()){
int u = q.front(); q.pop();
for (int i = ; i < G[u].size(); i++){
Edge& e = edge[G[u][i]];
if (!vis[e.to] && e.cap > e.flow){
d[e.to] = d[u] + ;
vis[e.to] = ;
q.push(e.to);
}
}
}
return vis[t];
} int dfs(int x, int a){
if (x == t || a == ) return a;
int flow = , f;
for (int& i = cur[x]; i < G[x].size(); i++){
Edge& e = edge[G[x][i]];
if (d[x] + == d[e.to] && (f = dfs(e.to, min(e.cap - e.flow, a))) > ){
e.flow += f;
edge[G[x][i]^].flow -= f;
flow += f;
a -= f;
if (a == ) break;
}
}
return flow;
} inline int dinic(){
int ans = ;
while(BFS()){
memset(cur, , sizeof(cur));
ans += dfs(, INF);
}
return ans;
} int main(){
read(n); read(m);
for (int i = ; i < m; i++){
int x, y;
read(x); read(y);
flag[x][y] = -;
}
cnt = ;
w = (n * n + )/ + ;
for (int i = ; i <= n; i++)
for (int j = ; j <= n; j++)
if ((i + j)% == ){
if (flag[i][j] != -) flag[i][j] = cnt;
cnt++;
}
else{
if (flag[i][j] != -) flag[i][j] = w;
w++;
}
s = , t = n*n + ;
build();
printf("%d", n*n - m - dinic());
return ;
}
然而这道题最开始写的时候TLE了
然后就加了当前弧优化
然后就A了（滑稽
但是可以看得出来非常的慢
测试点#kni0.in 结果:AC 内存使用量: 1512kB 时间使用量: 1ms
测试点#kni1.in 结果:AC 内存使用量: 1388kB 时间使用量: 1ms
测试点#kni10.in 结果:AC 内存使用量: 7256kB 时间使用量: 415ms
测试点#kni2.in 结果:AC 内存使用量: 1516kB 时间使用量: 1ms
测试点#kni3.in 结果:AC 内存使用量: 1644kB 时间使用量: 1ms
测试点#kni4.in 结果:AC 内存使用量: 1772kB 时间使用量: 3ms
测试点#kni5.in 结果:AC 内存使用量: 1772kB 时间使用量: 4ms
测试点#kni6.in 结果:AC 内存使用量: 1768kB 时间使用量: 2ms
测试点#kni7.in 结果:AC 内存使用量: 2020kB 时间使用量: 4ms
测试点#kni8.in 结果:AC 内存使用量: 4444kB 时间使用量: 143ms
测试点#kni9.in 结果:AC 内存使用量: 11732kB 时间使用量: 927ms
然后上网搜了一下其他的题解，发现其他的代码都跑得很快，然后就把建图方式改了一下
#include <cstdio>
#include <vector>
#include <cstring>
#include <algorithm>
#include <queue>
#include <iostream>
using namespace std;
const int N = ; int n, m, cnt, w; struct Edge{
int from, to, cap, flow;
};
vector < int > G[N*N];
vector < Edge > edge;
bool vis[N*N];
int s, t, d[N*N], cur[N*N], INF = (<<), flag[N][N], b[N*N];
int py[][] = {{, }, {, -}, {-, }, {-, -}, {, }, {, -}, {-, }, {-, -}}; inline void read(int &ans){
static char buf = getchar();
register int neg = ;
ans = ;
for (;!isdigit(buf); buf = getchar())
if (buf == '-') neg = -;
for (;isdigit(buf); buf = getchar())
ans = ans* + buf - '';
ans *= neg;
} inline void Add(int from, int to, int cap){
edge.push_back((Edge){from, to, cap, });
edge.push_back((Edge){to, from, , });
int m = edge.size();
G[from].push_back(m - );
G[to].push_back(m - );
} bool ok(int x, int y){
if (x > && x <= n && y > && y <= n)
if (flag[x][y] != -)
return true;
return false;
} inline int hash(int i,int j){
return (i - )*n + j;
} inline bool BFS(){
memset(vis, , sizeof(vis));
memset(d, 0xff, sizeof(d));
queue < int > q;
q.push(s);
d[s] = ;
vis[s] = ;
while(!q.empty()){
int u = q.front(); q.pop();
for (int i = ; i < G[u].size(); i++){
Edge& e = edge[G[u][i]];
if (!vis[e.to] && e.cap > e.flow){
d[e.to] = d[u] + ;
vis[e.to] = ;
q.push(e.to);
}
}
}
return vis[t];
} int dfs(int x, int a){
if (x == t || a == ) return a;
int flow = , f;
for (int& i = cur[x]; i < G[x].size(); i++){
Edge& e = edge[G[x][i]];
if (d[x] + == d[e.to] && (f = dfs(e.to, min(e.cap - e.flow, a))) > ){
e.flow += f;
edge[G[x][i]^].flow -= f;
flow += f;
a -= f;
if (a == ) break;
}
}
return flow;
} inline int dinic(){
int ans = ;
while(BFS()){
memset(cur, , sizeof(cur));
ans += dfs(, INF);
}
return ans;
} int main(){
read(n); read(m);
for (int i = ; i < m; i++){
int x, y;
read(x); read(y);
b[hash(x, y)] = ;
}
cnt = ;
s = , t = n*n + ;
for(int i = ; i <= n;i++)
for(int j = ; j <=n; j++){
if(!b[hash(i,j)] && ((i+j)&)){
Add(s, hash(i,j), );
if(i > && j > && !b[hash(i-,j-)])
Add(hash(i,j), hash(i-,j-), INF);
if(i > && j + <= n && !b[hash(i-,j+)])
Add(hash(i,j), hash(i-,j+), INF);
if(i > && j > && !b[hash(i-,j-)])
Add(hash(i,j), hash(i-,j-), INF);
if(i > && j + <= n &&!b[hash(i-,j+)])
Add(hash(i,j), hash(i-,j+), INF);
if(i + <= n && j > && !b[hash(i+,j-)])
Add(hash(i,j), hash(i+,j-), INF);
if(i + <= n && j + <= n && !b[hash(i+,j+)])
Add(hash(i,j), hash(i+,j+), INF);
if(i + <= n && j > && !b[hash(i+,j-)])
Add(hash(i,j), hash(i+,j-), INF);
if(i + <= n && j + <= n && !b[hash(i+,j+)])
Add(hash(i,j), hash(i+,j+), INF);
}
if(!b[hash(i,j)] && !((i+j)&)) Add(hash(i,j), t, );
} printf("%d", n*n - m - dinic());
return ; }
修改之后
测试点#kni0.in 结果:AC 内存使用量: 1640kB 时间使用量: 2ms
测试点#kni1.in 结果:AC 内存使用量: 1512kB 时间使用量: 2ms
测试点#kni10.in 结果:AC 内存使用量: 7256kB 时间使用量: 178ms
测试点#kni2.in 结果:AC 内存使用量: 1512kB 时间使用量: 2ms
测试点#kni3.in 结果:AC 内存使用量: 1640kB 时间使用量: 2ms
测试点#kni4.in 结果:AC 内存使用量: 1772kB 时间使用量: 2ms
测试点#kni5.in 结果:AC 内存使用量: 1772kB 时间使用量: 2ms
测试点#kni6.in 结果:AC 内存使用量: 1772kB 时间使用量: 2ms
测试点#kni7.in 结果:AC 内存使用量: 2020kB 时间使用量: 4ms
测试点#kni8.in 结果:AC 内存使用量: 4568kB 时间使用量: 92ms
测试点#kni9.in 结果:AC 内存使用量: 11608kB 时间使用量: 52ms
少了一个二维循环 + 减少了常数
结果快了1200ms（一脸懵逼
「CODVES 1922 」骑士共存问题（二分图的最大独立集|网络流）&dinic的更多相关文章
- loj #6226. 「网络流 24 题」骑士共存问题
#6226. 「网络流 24 题」骑士共存问题 题目描述 在一个 n×n\text{n} \times \text{n}n×n 个方格的国际象棋棋盘上,马(骑士)可以攻击的棋盘方格如图所示.棋盘上 ...
- 「AHOI2014/JSOI2014」骑士游戏
「AHOI2014/JSOI2014」骑士游戏 传送门 考虑 \(\text{DP}\). 设 \(dp_i\) 表示灭种(雾)一只编号为 \(i\) 的怪物的代价. 那么转移显然是: \[dp_i ...
- 【刷题】LOJ 6226 「网络流 24 题」骑士共存问题
题目描述 在一个 \(\text{n} \times \text{n}\) 个方格的国际象棋棋盘上,马(骑士)可以攻击的棋盘方格如图所示.棋盘上某些方格设置了障碍,骑士不得进入. 对于给定的 \(\t ...
- 「日常温习」Hungary算法解决二分图相关问题
前言 二分图的重点在于建模.以下的题目大家可以清晰的看出来这一点.代码相似度很高,但是思路基本上是各不相同. 题目 HDU 1179 Ollivanders: Makers of Fine Wands ...
- 洛谷P3355 骑士共存问题 二分图_网络流
Code: #include<cstdio> #include<cstring> #include<queue> #include<vector> #i ...
- 【wikioi】1922 骑士共存问题（网络流/二分图匹配）
用匈牙利tle啊喂?和网络流不都是n^3的吗(匈牙利O(nm), isap O(n^2m) 但是isap实际复杂度很优的(二分图匹配中,dinic是O(sqrt(V)*E),不知道isap是不是一样. ...
- 「CH6901」骑士放置
「CH6901」骑士放置 传送门 将棋盘黑白染色,发现"日"字的两个顶点刚好一黑一白,构成一张二分图. 那么我们将黑点向源点连边,白点向汇点连边,不能同时选的一对黑.白点连边. 当 ...
- 「THUWC 2017」随机二分图
「THUWC 2017」随机二分图 解题思路 : 首先有一个 \(40pts\) 的做法: 前 \(20pts\) 暴力枚举最终的匹配是怎样的,check一下计算方案数,后 \(20pts\) 令 \ ...
- # 「NOIP2010」关押罪犯（二分图染色+二分答案）
「NOIP2010」关押罪犯(二分图染色+二分答案) 洛谷 P1525 描述:n个罪犯(1-N),两个罪犯之间的仇恨值为c,m对仇恨值,求怎么分配使得两件监狱的最大仇恨值最小. 思路:使最大xxx最小 ...
随机推荐
- Laravel Session 遇到的坑
这两天遇到了一个很奇怪的问题,更新session ,session的值不变.经过一番追查,终于找到问题,并搞明白了原理.写这篇博客记录下. 框架版本 Laravel 5.4 问题 先来描述下问题,我在 ...
- 泛型加委托在EF下的操作例子
接下来放一个用SqlBulkCopy插入数据的例子,运用了泛型委托和反射.就当好好的运用这些知识. public static void AddEntityByBulk(IList entitys,s ...
- JavaWeb之session
Session是服务器端技术 利用这个技术,服务器在运行时可以为每一个用户的浏览器创建一个其独享的session对象,由于session为用户浏览器独享,所以用户在访问服务器的web资源时,可以把各自 ...
- Access-自定义控件TabControl
p{ font-size: 15px; } .alexrootdiv>div{ background: #eeeeee; border: 1px solid #aaa; width: 99%; ...
- MySQL flashback 功能
1. 简介 mysqlbinlog flashback(闪回)用于快速恢复由于误操作丢失的数据.在DBA误操作时,可以把数据库恢复到以前某个时间点(或者说某个binlog的某个pos).比如忘了带wh ...
- 云计算之路-阿里云上：数据库连接数过万的真相，从阿里云RDS到微软.NET Core
在昨天的博文中,我们坚持认为数据库连接数过万是阿里云RDS的问题,但后来阿里云提供了当时的数据库连接情况,让我们动摇了自己的想法. 帐户 连接数 A 4077 B 3995 C 741 D 698 E ...
- Hibernate基础学习(二)—Hibernate相关API介绍
一.Hibernate的核心接口 所有的Hibernate应用中都会访问Hibernate的5个核心接口. (1)Configuration接口: 配置Hibernate,启动Hi ...
- 20170410Linux备课资料 --- 压缩与解压缩
这节课我们来学习一下压缩与解压缩,那什么是压缩与解压缩呢? 联想一下Windows系统: 选中文件,右键选择即可 如果压缩,可以选择要压缩的格式,而解压缩直接选择就可以完成了 Linux是通过命令的方 ...
- PAT 1046
1046. Shortest Distance (20) The task is really simple: given N exits on a highway which forms a sim ...
- LINUX ON AZURE 安全建议（全）
本文为个人原创,可以自由转载,转载请注明出处,多谢! 本文地址:http://www.cnblogs.com/taosha/p/6399554.html 1.网络与安全规划 Azure 虚拟网络 (V ...