浅读K-means
百度百科释义为
问题
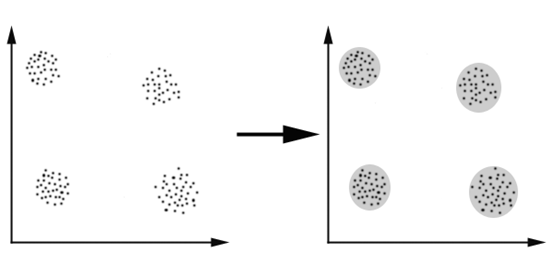

工作原理
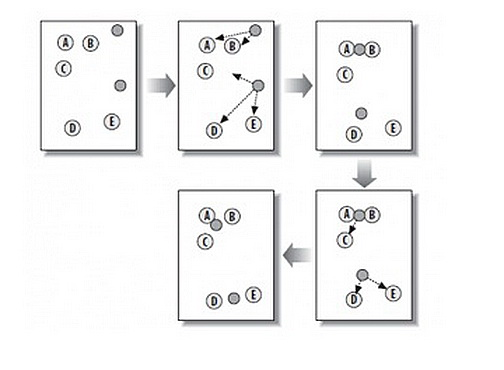 K-Means算法概要
K-Means算法概要工作过程k-means 算法的工作过程
算法优点
算法缺点
浅读K-means的更多相关文章
- Handlebars模板引擎中的each嵌套及源码浅读
若显示效果不佳,可移步到愚安的小窝 Handlebars模板引擎作为时下最流行的模板引擎之一,已然在开发中为我们提供了无数便利.作为一款无语义的模板引擎,Handlebars只提供极少的helper函 ...
- 小王子浅读Effective javascript(一)了解javascript版本
哈哈,各位园友新年快乐!愚安好久没在园子里写东西了,这次决定针对javascript做一个系列,叫做<小王子浅读Effective javascript>,主要是按照David Herma ...
- Spark 源码浅读-SparkSubmit
Spark 源码浅读-任务提交SparkSubmit main方法 main方法主要用于初始化日志,然后接着调用doSubmit方法. override def main(args: Array[St ...
- 浅读tomcat架构设计之tomcat生命周期(2)
浅读tomcat架构设计和tomcat启动过程(1) https://www.cnblogs.com/piaomiaohongchen/p/14977272.html tomcat通过org.apac ...
- 浅读tomcat架构设计之tomcat容器Container(3)
浅读tomcat架构设计和tomcat启动过程(1) https://www.cnblogs.com/piaomiaohongchen/p/14977272.html 浅读tomcat架构设计之tom ...
- 《Attention is All You Need》浅读(简介+代码)
2017年中,有两篇类似同时也是笔者非常欣赏的论文,分别是FaceBook的<Convolutional Sequence to Sequence Learning>和Google的< ...
- 浅谈k短路算法
An Old but Classic Problem 给定一个$n$个点,$m$条边的带正权有向图.给定$s$和$t$,询问$s$到$t$的所有权和为正路径中,第$k$短的长度. Notice 定义两 ...
- 【原理】Java的ThreadLocal实现原理浅读
当前线程的值传递,ThreadLocal 通过ThreadLocal设值,在线程内可获取,即时获取值时在其它Class或其它Method. public class BasicUsage { priv ...
- KNN 与 K - Means 算法比较
KNN K-Means 1.分类算法 聚类算法 2.监督学习 非监督学习 3.数据类型:喂给它的数据集是带label的数据,已经是完全正确的数据 喂给它的数据集是无label的数据,是杂乱无章的,经过 ...
随机推荐
- 微信小程序(一)基本知识初识别
最近微信圈里小程序很火的样子,以前小程序刚开始的时候研究了一下,多日没关注发现一些东西都淡忘了,最后决定还是记录下来的好. 毕竟好记星比不上烂笔头嘛~ 另外有想学习小程序的同学,也可以参考下,当然如果 ...
- 有关java 8
http://www.iteye.com/news/27608 Java 8 发布时间敲定,延期半年 http://www.iteye.com/news/24631/ Java 8 的重要 ...
- Java中的clone()----深复制,浅复制
这篇文章主要介绍了Java中对象的深复制(深克隆)和浅复制(浅克隆) ,需要的朋友可以参考下 1.浅复制与深复制概念 ⑴浅复制(浅克隆) 被复制对象的所有变量都含有与原来的对象相同的值,而所有的对其他 ...
- business meeting
Metting are all about discussions . discussion expression 开始会议 Let's get started We need to discuss. ...
- 通过前端sdk 做facebook登录
1.首先通过前端FB.init初始化,其中很重要的参数就是appId,该参数需要在facebook developer平台申请,创建应用,添加相应的ip 地址或者域名. 2.引入facebook 提供 ...
- react 入门教程 阮一峰老师真的是榜样
- 转自阮一峰老师博客 React 入门实例教程 作者: 阮一峰 日期: 2015年3月31日 现在最热门的前端框架,毫无疑问是 React . 上周,基于 React 的 React Nati ...
- 花了一年时间开发的TTFEditor 字体编辑器
TTF(True Type Font)字库是微软定义的基于windows的标准字库格式.但其由于专利保护以及无法跨平台导致TTF字库在实际应用中无法有效使用. 为此我推出TTFEditor字体编辑软件 ...
- Redis-消息发布与订阅
redis的消息发布与订阅适合做在线聊天, 消息推送 使用方法: 发布端: publish +频道名称 + 发布内容 订阅端: subscribe + 频道名称 发布端例子: 127.0.0.1:63 ...
- ABAP中Collect的用法
vaule:collect在非数值字段相同的情况下,起到了数值字段汇总作用. 非数值字段不同的情况下,效果和append相同执行插入内表操作,当非数值字段相同的时候,则相当于modify的效果,只不过 ...
- 放开那个UI 妹子,让我来(上)
一.前言 今天要学习的内容:今天主要是稍微总结一下,页面中如何用字体代替图片,省事,省时,方便,实用! 小苏啰嗦:人都是有惰性的.真的.刚开始我们有一个经验丰富的美工,加上我们关系又非常好,以至于每次 ...
