hdu 6171---Admiral(双向搜索)

题目链接

Problem Description

Suppose that you are an admiral of a famous naval troop. Our naval forces have got 21 battleships. There are 6 types of battleships.
First, we have got one flagship in which the admiral must be and it is denoted by number 0. Others are denoted by number from 1 to 5, each of them has 2, 3, 4, 5, 6 ships of its kind. So, we have got 21 battleships in total and we must take a giant battle against the enemy. Hence, the correct strategy of how to arrange each type of battleships is very important to us.
The shape of the battlefield is like the picture that is shown below.
To simplify the problem, we consider all battleships have the same rectangular shape.

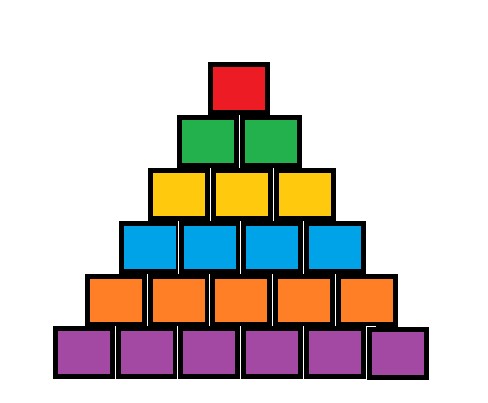
Fortunately, we have already known the optimal state of battleships.
As you can see, the battlefield consists of 6 rows. And we have 6 types of battleship, so the optimal state is that all the battleships denoted by number i are located at the i-th row. Hence, each type of battleship corresponds to different color.
You are given the initial state of battlefield as input. You can change the state of battlefield by changing the position of flagship with adjacent battleship.
Two battleships are considered adjacent if and only if they are not in the same row and share parts of their edges. For example, if we denote the cell which is at i-th row and j-th position from the left as (i,j), then the cell (2,1) is adjacent to the cells (1,0), (1,1), (3,1), (3,2).
Your task is to change the position of the battleships minimum times so as to reach the optimal state.
Note: All the coordinates are 0-base indexed.

 

Input

The first line of input contains an integer T (1 <= T <= 10), the number of test cases. 
Each test case consists of 6 lines. The i-th line of each test case contains i integers, denoting the type of battleships at i-th row of battlefield, from left to right.

 

Output

For each test case, if you can’t reach the goal in no more than 20 moves, you must output “too difficult” in one line. Otherwise, you must output the answer in one line.

 

Sample Input

1

1

2 0

2 1 2

3 3 3 3

4 4 4 4 4

5 5 5 5 5 5

 

Sample Output

3

 

题意：有21个数由1个0、2个1、3个2、4个3、5个4和6个5组成，这21个数构成一个三角形，与杨辉三角一样第一行1个数，第2行2个数……第6行6个数，现在要把这21个数归位按顺序摆好，0 在第一行，1在第二行……5在第六行，每次操作为0与它相邻的数可以进行交换，同行之间不能进行交换，求最少经过多少步将所有数归位，如果20步还我完成不了则输出“too difficult”。

 

思路：搜索，但是直接搜20步会超时，所以可以从两端各搜10步，这样就降低了复杂度，另外可以用hash来保存状态。

 

代码如下：

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <queue>
#include <map>
using namespace std;
typedef long long LL;
int dx[]={,,-,-};
int dy[]={,,-,};
struct Node{
    LL p[][];
    int r,c;
    int flag;
    int dept;
};
queue<Node>Q;
map<LL,int>M[];
LL cal(Node a)
{
    LL ans=;
    for(int i=;i<;i++)
    {
        for(int j=;j<=i;j++)
        {
            ans=ans*+a.p[i][j];
        }
    }
    return ans;
}
int bfs(Node &s,Node &e)
{
    while(!Q.empty()) Q.pop();
    M[].clear(); M[].clear();
    M[][cal(s)]=;
    M[][cal(e)]=;
    Q.push(s);
    Q.push(e);
    while(!Q.empty())
    {
        Node x=Q.front(); Q.pop();
        LL sta=cal(x);
        if(M[!x.flag].count(sta))
        {
            int num=M[!x.flag][sta]+x.dept;
            if(num<=) return num;
            else continue;
        }
        if(x.dept>=) continue;
        for(int i=;i<;i++)
        {
            Node y=x;
            y.dept++;
            y.r+=dx[i];
            y.c+=dy[i];
            if(y.r< || y.r>= || y.c< || y.c>y.r) continue;
            swap(y.p[x.r][x.c],y.p[y.r][y.c]);
            if(M[y.flag].count(cal(y))==) M[y.flag][cal(y)]=y.dept;
            Q.push(y);
        }
    }
    return -;
}

int main()
{
    int T; cin>>T;
    Node s,e;
    while(T--)
    {
        for(int i=;i<;i++)
        {
            for(int j=;j<=i;j++)
            {
                scanf("%lld",&s.p[i][j]);
                if(s.p[i][j]==) s.r=i, s.c=j;
                e.p[i][j]=i;
            }
        }
        s.flag=; s.dept=;
        e.r=; e.c=;
        e.flag=; e.dept=;
        int ans=bfs(s,e);
        if(ans>=&&ans<=) printf("%d\n",ans);
        else puts("too difficult");
    }
    return ;
}
/**
1
2 1
2 0 2
3 3 3 3
4 4 4 4 4
5 5 5 5 5 5
0
1 1
2 2 2
3 3 3 3
4 4 4 4 4
5 5 5 5 5 5
*/