从马尔可夫模型(Markov Model)到隐马尔可夫模型(Hidden Markov Model)

1、参考资料：

博客园 - 刘建平随笔：https://www.cnblogs.com/pinard/p/6945257.html

哔站up主 - 白手起家的百万富翁：https://www.bilibili.com/video/BV1DK411W7jJ?from=search&seid=2670213518419567446

哔站up主 - asia1987：https://www.bilibili.com/video/BV13C4y1W7iB/?spm_id_from=trigger_reload

2、马尔可夫模型(MM)

如下图例子1：先玩-->再吃-->再睡，就是一条马尔科夫链，是可观测到的，我们可以直接求解这条马尔科夫链的概率。

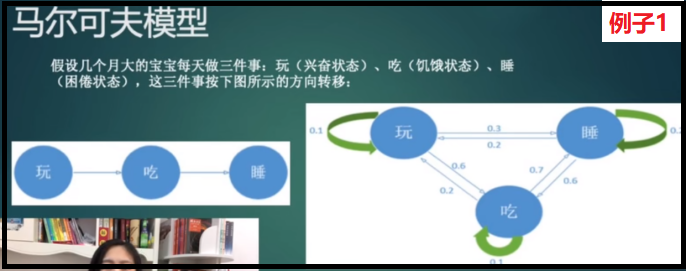
如下图例子2：天气情况是可观测的，已知晴天、多云、雨天之间的转换概率，如果今天是晴天，就可以推断出明天各种天气的概率，同样后天的天气可以由明天的天气进行计算。

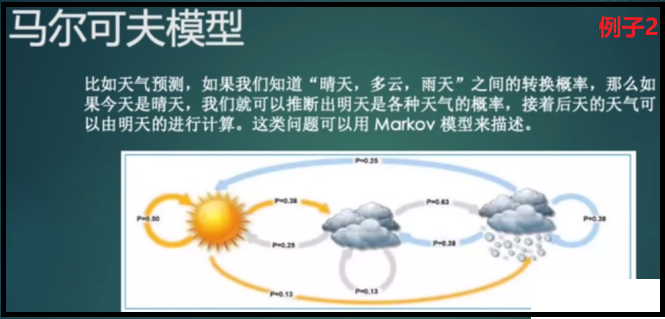
 3、隐马尔可夫模型(HMM)

如下图例子2变形：天气情况是不可观测的（即隐藏状态），但我们发现水藻的干燥与否和天气有关，而水藻又是可观测的，我们可以通过水藻来推测这三天的天气情况。

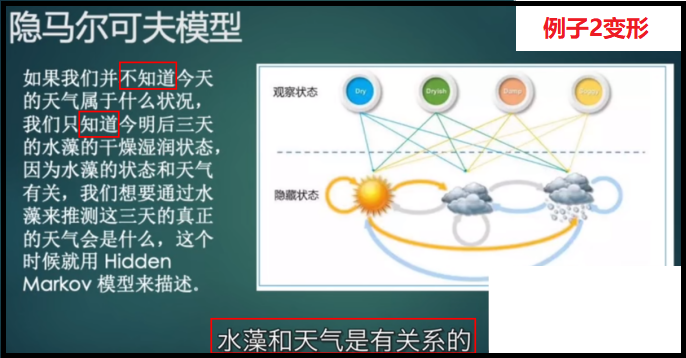
从上面的例子我们不难看出：隐马尔可夫模型是根据我们可见的东西（水藻）去推测我们真正想要的东西（天气）。

4、HMM五元组、三要素

• 观测序列-O (水藻状态，可观测)               (序列长度：任意)
• (隐藏)状态序列-I (天气状态，不可观测)     (序列长度：任意，目前看下来其长度同观测序列)
• 初始状态概率向量-Π                              (向量大小：(1*N)^T)
• 状态转移概率矩阵-A                              (矩阵大小：状态N*状态N)
• 观测状态概率矩阵-B (也叫发射矩阵B)        (矩阵大小：状态N*观测M)

其中后三项为HMM的三要素：λ=(Π,A,B)

 5、HMM两个基本假设

• 齐次马尔可夫性假设（一阶马尔可夫假设）：当前时刻的隐藏状态，只依赖于上一时刻的隐藏状态，与其它时刻状态和观测值都是无关的。
• 观测独立性假设（隐藏状态假设）：当前时刻的观测值，只依赖于当前时刻的隐藏状态，与其它时刻状态和观测值都是无关的。

PS：还有一种说法，多了一个转换函数稳定性假设。

6、应用HMM来求解的三个基本问题

• 概率计算：给定模型λ=(π,A,B)和观测序列O，求观测序列O出现的概率。           (前向-后向算法)
• 解码问题：给定模型λ=(π,A,B)和观测序列O，求概率最大的隐藏状态序列I。      (viterbi算法)
• 学习问题：给定观测序列O，求观测序列O概率最大时模型λ=(π,A,B)的参数。   (极大似然估计算法)

7、实例一

有三个骰子（D4四面体，D6六面体，D8八面体），每个面都写有一个数字（如下图），进行有放回的抽样。

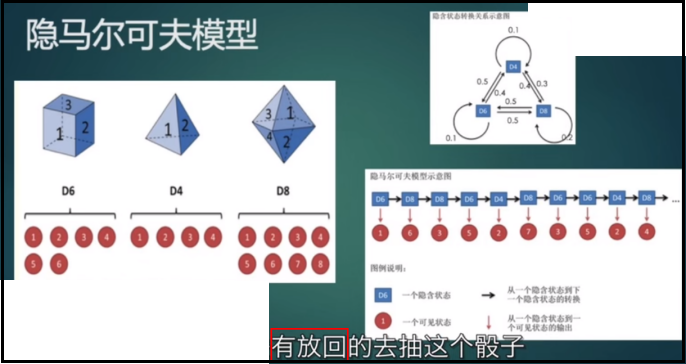
由上可知：观测值是骰子上的数字，有8种，即M=8；隐藏状态是几面体骰子，有3种，即N=3；

按照HMM五元组：

• 在完成一轮有放回抽样，我们可以得到一个观测序列O如下
• 隐藏状态序列 I 未知，待求
• 初始状态概率向量π如下，一般平均初始化
• 状态转移概率矩阵A如下，一般经验、统计得到
• 观测概率分布矩阵B如下，一般经验或按照实际情况计算得到

8、实例二

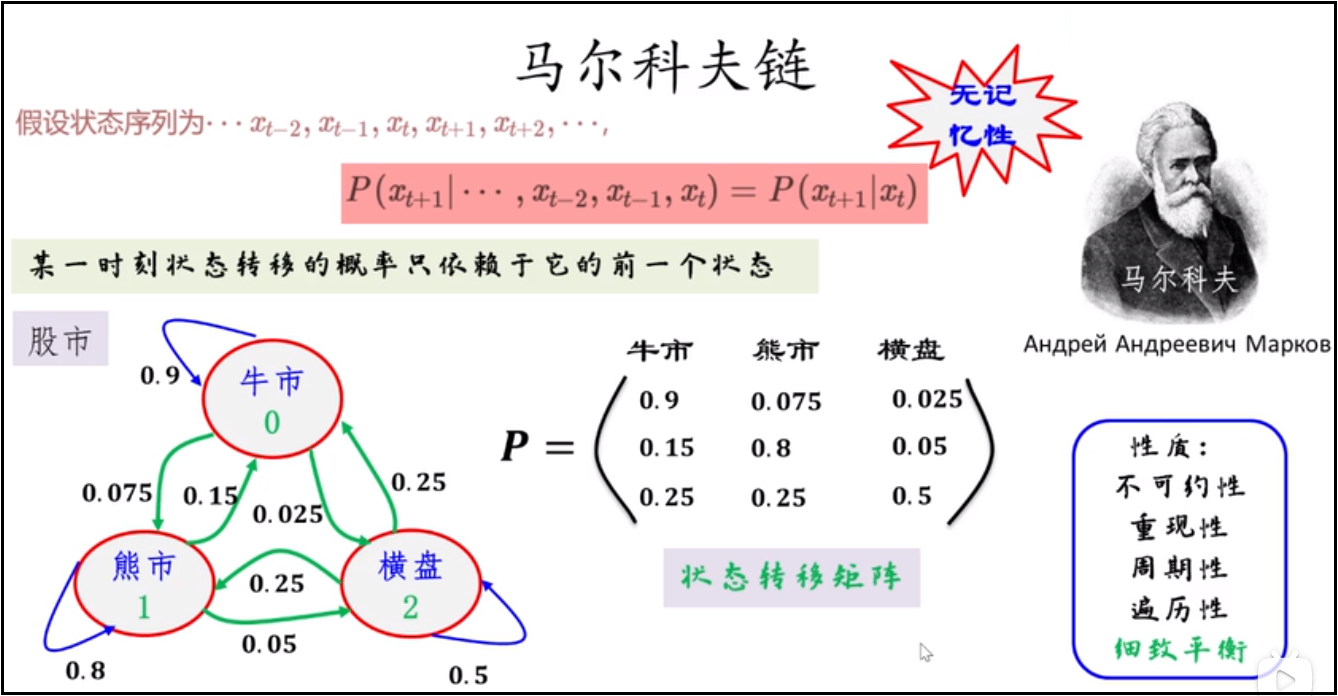
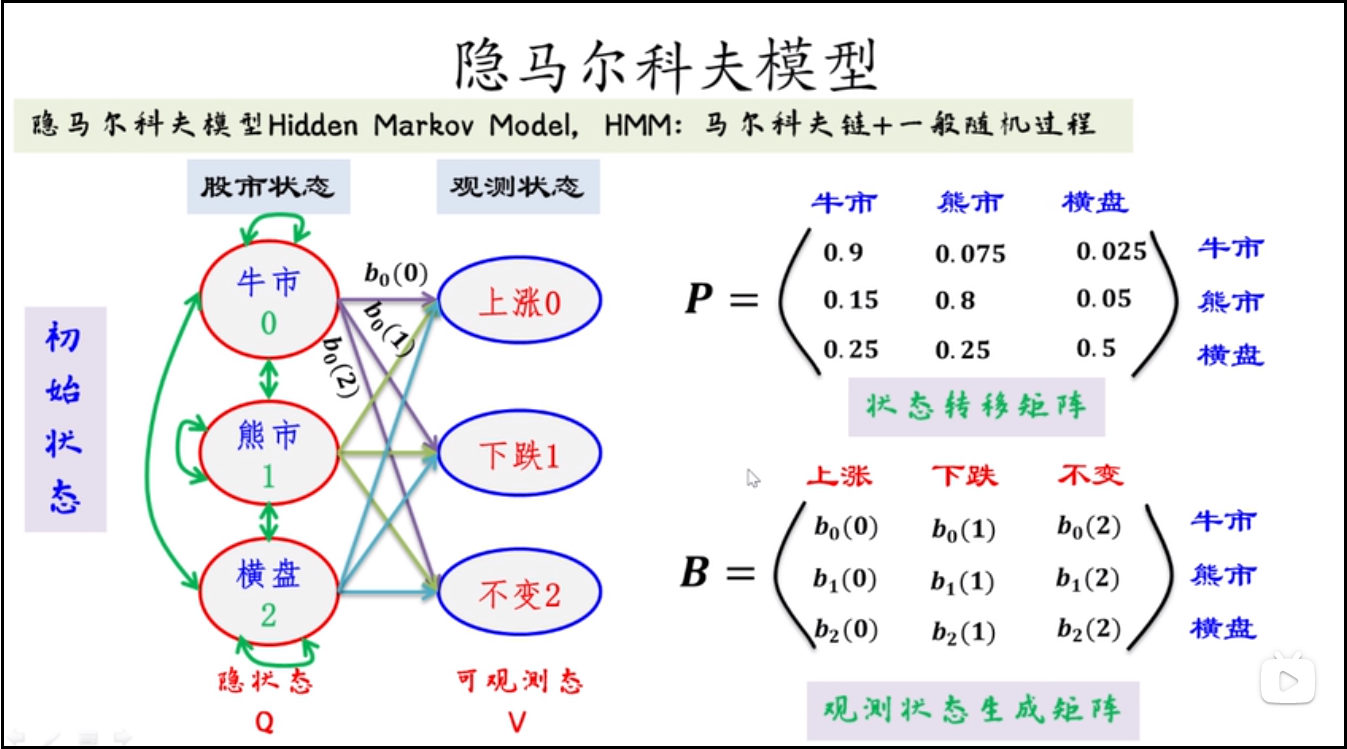
股市有三种隐藏状态（牛市、熊市、横盘），有三种观测状态（上涨、下跌、不变），HMM五元组如下图。