二叉树遍历-c实现

这里主要是三种遍历，先序（preorder，NLR），中序（Inorder，LNR），后序（Postorder，LRN）

N：node，L：left，R：right

基本排序：先序（NLR，节点，左，右），中序（LNR，左，节点，右），后序（LRN，左，右，节点）

要点：在每一种排序里，必须遵守基本排序。看图：

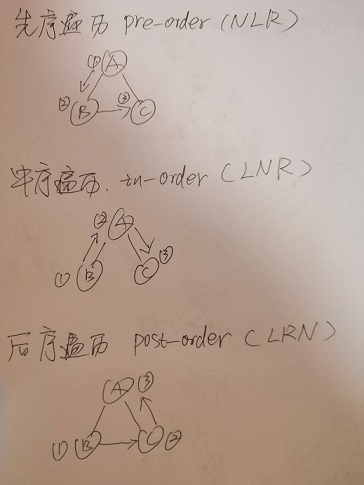
为了更加直观的了解，看下面的c语言实现的代码，参考了：https://www.geeksforgeeks.org/tree-traversals-inorder-preorder-and-postorder/

#include<cstdio>
#include<cstdlib>
using namespace std;
struct node{
    int data;
    struct node* left;
    struct node* right;
};
struct node* newNode(int data){
    struct node* node = (struct node*)malloc(sizeof(struct node));
    node->data=data;
    node->left=NULL;
    node->right=NULL;
    return node;
}
void printPostorder(struct node* node){
    if(node == NULL)
        return;
    printPostorder(node->left);
    printPostorder(node->right);
    printf("%d ",node->data);
}
void printInorder(struct node* node){
    if(node==NULL){
        return;
    }
    printInorder(node->left);
    printf("%d ",node->data);
    printInorder(node->right);
}
void printPreorder(struct node* node){
    if(node==NULL){
        return;
    }
    printf("%d ",node->data);
    printPreorder(node->left);
    printPreorder(node->right);
}
int main(){
    struct node *root=newNode();
    root->left=newNode();
    root->right=newNode();
    root->left->left=newNode();
    root->left->right=newNode();
    root->right->left=newNode();
    root->right->right=newNode();
    root->left->left->left=newNode();
    root->left->left->right=newNode();
    root->left->right->left=newNode();
    root->left->right->right=newNode();
    root->right->left->left=newNode();
    root->right->left->right=newNode();
    root->right->right->left=newNode();
    root->right->right->right=newNode();
    printf("\nPreorder raversal of binary tree is \n");
    printPreorder(root);
    printf("\nInorder raversal of binary tree is \n");
    printInorder(root);
    printf("\nPostorder raversal of binary tree is \n");
    printPostorder(root);
    return ;
}

输出：

Preorder raversal of binary tree is
 
Inorder raversal of binary tree is
 
Postorder raversal of binary tree is
              

写一个中序输出的图解：