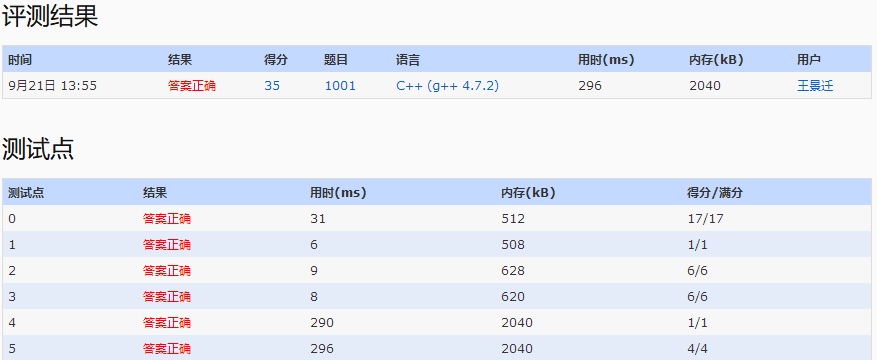
PAT-Top1001. Battle Over Cities - Hard Version (35)

　　在敌人占领之前由城市和公路构成的图是连通图。在敌人占领某个城市之后所有通往这个城市的公路就会被破坏，接下来可能需要修复一些其他被毁坏的公路使得剩下的城市能够互通。修复的代价越大，意味着这个城市越重要。如果剩下的城市无法互通，则说明代价无限大，这个城市至关重要。最后输出的是代价最大的城市序号有序列表。借助并查集和Kruskal算法（最小生成树算法）来解决这个问题。

 //#include "stdafx.h"
 #include <iostream>
 #include <algorithm>
 #include <vector>

 using namespace std;

 struct edge { // edge struct
     int u, v, cost;
 };
 vector<edge> edges; // the number of edges is greater than 500 far and away

 int cmp(edge a, edge b) { // sort rule
     return a.cost < b.cost;
 }

 int parent[]; // union-find set

 void initParent(int n) { // initialize union-find set
     int i;
     for(i = ; i <= n; i++) {
         parent[i] = -; // a minus means it is a root node and its absolute value represents the number of the set
     }
 }

 int findRoot(int x) { // find the root of the set
     int s = x;
     while(parent[s] > ) {
         s = parent[s];
     }

     int temp;
     while(s != x) { // compress paths for fast lookup
         temp = parent[x];
         parent[x] = s;
         x = temp;
     }

     return s;
 }

 void unionSet(int r1, int r2) { // union sets. More concretely, merge a small number of set into a large collection
     int sum = parent[r1] + parent[r2];
     if(parent[r1] > parent[r2]) {
         parent[r1] = r2;
         parent[r2] = sum;
     } else {
         parent[r2] = r1;
         parent[r1] = sum;
     }
 }

 int maxw = ; // max cost
 bool infw; // infinite cost

 int kruskal(int n, int m, int out) { // Kruskal algorithm to get minimum spanning tree
     initParent(n);

     int u, v, r1, r2, num = , i, w = ;
     for (i = ; i < m; i++) {
         u = edges[i].u;
         v = edges[i].v;

         if (u == out || v == out) {
             continue;
         }

         r1 = findRoot(u);
         r2 = findRoot(v);

         if (r1 != r2) {
             unionSet(r1, r2);
             num++;

             if (edges[i].cost > ) { // only consider the cost which is not zero
                 w += edges[i].cost;
             }

             if (num == n - ) {
                 break;
             }
         }
     }

     //printf("num %d\n", num);
     if (num < n - ) { // spanning tree is not connected
         w = -; // distinguish the situation of the occurrence of infinite cost

         if (!infw) { // when infinite cost first comes out
             infw = true;
         }
     }

     return w;
 }

 int main() {
     int n, m;
     scanf("%d%d", &n, &m);

     int i, status;
     edge e;
     for (i = ; i < m; i++) {
         scanf("%d%d%d%d", &e.u, &e.v, &e.cost, &status);
         if (status == ) {
             e.cost = ;
         }

         edges.push_back(e);
     }

     if (m > ) {
         sort(edges.begin(), edges.end(), cmp);
     }

     int curw, res[], index = ;
     for (i = ; i <= n; i++) { // traverse all vertices to obtain the target vertex
         curw = kruskal(n, m, i);
         if (!infw) { // when infinite cost doesn't come out
             if (curw < maxw) {
                 continue;
             }

             if (curw > maxw) {
                 index = ;
                 maxw = curw;
             }
             res[index++] = i;
         } else { // otherwise
             if (curw < ) {
                 if (maxw > ) {
                     maxw = -;
                     index = ;
                 } 

                 res[index++] = i;
             }
         }
     }

     if (index > ) {
         for (i = ; i < index; i++) {
             if (i > ) {
                 printf(" ");
             }
             printf("%d", res[i]);
         }
     } else {
         printf("");
     }
     printf("\n");

     system("pause");
     return ;
 }

　　

　　参考资料

pat-top 1001. Battle Over Cities - Hard Version (35)