决策树和基于决策树的集成方法（DT,RF,GBDT,XGB）复习总结

摘要：

　　1.算法概述

　　2.算法推导

　　3.算法特性及优缺点

　　4.注意事项

　　5.实现和具体例子

内容：

1.算法概述

　　1.1 决策树（DT）是一种基本的分类和回归方法。在分类问题中它可以认为是if-then规则的集合，也可以认为是定义在特征空间与类空间上的条件概率分布，学习思想包括ID3,C4.5,CART（摘自《统计学习方法》）。

　　1.2 Bagging :基于数据随机重抽样的集成方法（Ensemble methods），也称为自举汇聚法（boostrap aggregating）,整个数据集是通过在原始数据集中随机选择一个样本进行替换得到的。进而得到S个基预测器（ base estimators），选择estimators投票最多的类别作为分类结果，estimators的平均值作为回归结果。（摘自《统计学习方法》和scikit集成方法介绍）

　　1.3 随机森林（RF）：基于boostrap重抽样和随机选取特征，基预测器是决策树的集成方法（Ensemble methods）

　　1.4 Boosting :通过改变样本的权重（误分样本权重扩大）学习多个基预测器，并将这些预测器进行线性加权的集成方法 （摘自《统计学习方法》）

　　1.5 梯度提升决策树（GBDT）:基于boosting方法，提升方向是梯度方向的决策树的集成方法（Ensemble methods）

　　1.6 XGBDT:基于GBDT的一种升级版本，对目标函数做了二阶导数，主要改进是使用了正则化和特征分块存储并行处理（参考大杀器xgboost指南）

　　1.7 回归/分类树树模型函数：

，这里数据集被划分为R1,...,Rm个区域，每一个区域对应一个预测值Cm;其中I()是指示函数，当满足条件时返回1，否则为0

　　1.8 决策树常见的损失函数：

　　　　用于分类的损失函数：01损失，LR的对数损失，softmax的mlogloss

　　　　用于回归的损失函数：线性回归的MSE

2.算法推导

　　2.1 决策树生成过程就是一个递归的过程，如果满足某种停止条件（样本都是同一类别，迭代次数或者其他预剪枝参数）则返回多数投票的类作为叶结点标识；否则选择最佳划分特征和特征值生成|T|个子节点，对子节点数据进行划分；所以划分属性的计算方式是DT的精髓，以下总结各种划分属性的计算方法（附一个java实现决策树的demo）：

　　ID3与C4.5中使用的信息增益和信息增益率：

　　信息熵（Entropy）是表示随机变量不确定性的度量：

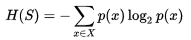　　　　，其中S是数据集，X是类别集合，p（x）是类别x占数据集的比值。

　　信息增益（Information gain）表示数据集以特征A划分，数据集S不确定性下降的程度

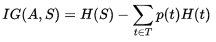　　　　，其中H(S)是原数据集S的熵；T是S以特征A划分的子集集合，即

　　　　p(t)是T的某一划分子集t占数据集S的比值，H(t)是划分子集t的熵。

　　 信息增益率（为了克服ID3倾向于特征值多的特征）：

　　　　IG_Ratio = IG(A,S) / H(S)，这里除以特征S的熵来"归一化"。　

　　  信息增益/信息增益率越大，样本集合的不确定性越小

　　 CART中使用的Gini指数：

　　　基尼（gini）指数是元素被随机选中的一种度量：

　　　数据集D的gini系数：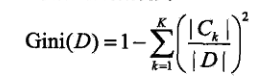

　　　在数据集D中以特征A划分的gini系数：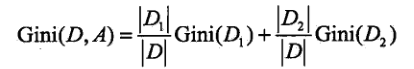

　　　gini指数越小，样本集合的不确定性越小

　　　

　　　2.2回归树：CART,R,GBDT以及XGBoost 都可以用作回归树，所以这里梳理下回归树是如何确定划分特征和划分值的：

　　　,其中C1,C2是划分区域R1,R2的均值，J,S是划分特征和划分的特征值

　　　2.3 GBDT算法（来自这个论文）

　　　

　　　

　　附：　

　　

　　　　参考自：《统计学习基础 数据挖据、推理与预测》 by Friedman 10.9节

　　　　2.4 XGBoost

　　　　模型函数：　　

　　　　　　　

　　　　最终得：

　　　　

　　　　详细的推导会附在文尾

3.算法特性及优缺点

　　决策树的优（特性）缺点：

　　   优点：

　　　　（1）输出结果易于理解，

　　　　（2）对缺失值不敏感，可以处理无关数据，可以处理非线性数据

　　　　（3）对于异常点的容错能力好，健壮性高

　　　　（4）不需要提前归一化

　　　　（5）可以处理多维度输出的分类问题。

　　　缺点：

　　　　（1）容易过拟合，需要剪枝或者RF避免

　　　　（2）只注重单个特征的局部划分，而不能想LR那样考虑整体的特征

　　　　（3）有些问题决策树很难表达，如：异或问题、奇偶校验或多路复用器问题

　　ID3算法比较：

　　　 缺点：

　　　　（1）按照特征切分后，特征不在出现，切分过于迅速；

　　　　（2）只能处理类别类型，决策树不一定是二叉树，导致学习出来的树可能非常宽

　　　　（3）不能回归

　　　　（4）信息增益的结果偏向于数值多的特征　　　

　　CART算法比较：

　　　　优点：离散或者连续特征可以重复使用；可以处理连续性特征；可以回归

　　RF的特性

　　　　优点：并行处理速度快，泛化能力强,可以很好的避免过拟合；能够得到特征的重要性评分（部分参考这篇总结）

　　　　　　　对于不平衡数据集可以平衡误差（参考中文维基百科）

　　　　缺点：偏差会增大（方差减小）

　　GBDT的特性

　　　　优点：精度高;可以发现多种有区分性的特征以及特征组合

　　　　缺点：串行处理速度慢

　　XGB算法比较：

　　　　使用了二阶导数，对特征分块，从而可以并行加快运算速度

4.注意事项

　　4.1 树的剪枝（结合sklearn中的参数进行总结）

　　　　　max_depth ：DT的最大深度（默认值是3）

　　　　　max_features ：最大特征数（默认值是None）

　　　　　min_samples_split ：触发分割的最小样本个数，如果是2，两个叶结点各自1个样本

　　　　　min_samples_leaf ：叶子节点的最小样本数，如果是2，两个叶结点至少2个样本

　　　　　min_impurity_split ：最小分割纯度（与分割标准有关，越大越不容易过拟合）　

　　　　（附：树模型调参）

　　4.2 如何计算的属性评分（结合sklearn总结）

　　　　　 The importance of a feature is computed as the (normalized) total reduction of the criterion brought by that feature. It is also known as the Gini importance [R245].

　　4.3 正则化

　　　　衰减（Shrinkage）因子（learning_rate）：

　　　　proposed a simple regularization strategy that scales the contribution of each weak learner by a factor :

　　　　The parameter  is also called the learning rate because it scales the step length the gradient descent procedure; it can be set via 　　　　the learning_rate parameter.  ——摘自scikit官网：

　　　　正则项系数：

• lambda [default=0]
  • L2 正则的惩罚系数
  • 用于处理XGBoost的正则化部分。通常不使用，但可以用来降低过拟合
• alpha [default=0] 
  
  • L1 正则的惩罚系数
  • 当数据维度极高时可以使用，使得算法运行更快。
• lambda_bias 
  
  • 在偏置上的L2正则。缺省值为0（在L1上没有偏置项的正则，因为L1时偏置不重要）   ——摘自XGBOOST调优

　　4.4 其他参数：

　　　　class_weight：为了克服类别不均衡问题，引入代价敏感方法，class_weight是各类别的权重

　　　　　　　

5.实现和具体例子

　　微额借款人品预测竞赛

　　风控违约预测竞赛

　　CTR预测（GBDT+LR）

　　Spark ml GradientBoostedTrees 核心实现部分

　　预测多变量的例子——(kaggle)预测沃尔玛超市38个购物区购物量

附：XGB推导目标函数推导：