CodeForces 703C Chris and Road

数学，递推。

不知道有没有更加神奇的做法，我是这样想的：

首先，如果多边形完全在$y$轴左侧，那么答案为$\frac{w}{u}$。

剩下的情况就要先判断是否能在车开过之前跑过去，如果跑不过去，要在车慢慢开过$y$轴的时候，一起慢慢跑上去。

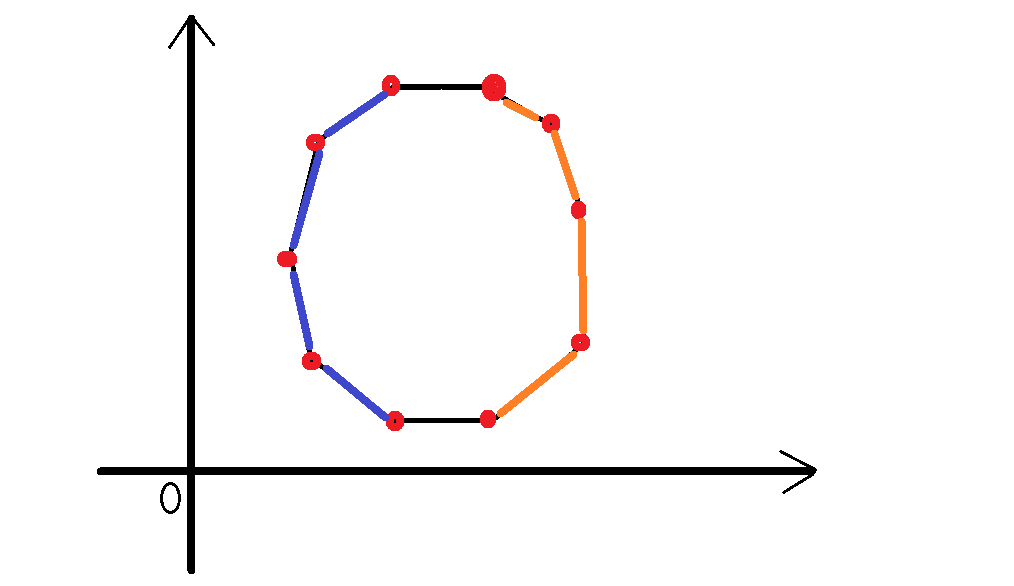
那么先来判断是否能在车开过之前跑过去：

如上图所示，如果要在车来车前跑过去，那么等价于要求：对于凸包左侧蓝色链上的每一个点$L[i]$，满足$\frac{{L[i].y}}{u} ≤ \frac{{L[i].x}}{v}$，即人要比点先到。如果有一个点不满足，那么就人就无法在车来前跑过去。如果可以的话，答案为$\frac{w}{u}$。

剩下的情况就是凸包右侧黄色链开过$y$轴时，人同时走上去。这种情况的答案，递推一下就能算出来了，如果人走到$(0,R[i].y)$所花的时间为$ans$，那么人走到$(0,R[i+1].y)$的时间$ans$更新为$\max (ans + \frac{{\left( {R\left[ {i + 1} \right].y-R\left[ i \right].y } \right)}}{u},\frac{{R[i].x}}{v})$，想一想也能想明白吧~

#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<vector>
#include<map>
#include<set>
#include<queue>
#include<stack>
#include<iostream>
using namespace std;
typedef long long LL;
const double pi=acos(-1.0),eps=1e-;
void File()
{
    freopen("D:\\in.txt","r",stdin);
    freopen("D:\\out.txt","w",stdout);
}

const int INF=;
const int maxn=;
int n,w,v,u,len1,len2;
struct X { int x,y; }p[maxn],L[maxn],R[maxn];

int main()
{
    scanf("%d%d%d%d",&n,&w,&v,&u);
    for(int i=;i<=n;i++) scanf("%d%d",&p[i].x,&p[i].y);

    int ymin=INF,ymax=-INF,f,p1,p2; bool flag;
    for(int i=;i<=n;i++) ymin=min(ymin,p[i].y), ymax=max(ymax,p[i].y);
    f=INF; for(int i=;i<=n;i++) if(p[i].y==ymin&&p[i].x<f) f=p[i].x,p1=i;
    f=INF; for(int i=;i<=n;i++) if(p[i].y==ymax&&p[i].x<f) f=p[i].x,p2=i;

    flag=; for(int i=p1;i>=;i--) { L[len1++]=p[i]; if(i==p2) { flag=; break; } }
    if(flag==) for(int i=n;i>=p2;i--) L[len1++]=p[i];

    f=-INF; for(int i=;i<=n;i++) if(p[i].y==ymin&&p[i].x>f) f=p[i].x,p2=i;
    f=-INF; for(int i=;i<=n;i++) if(p[i].y==ymax&&p[i].x>f) f=p[i].x,p1=i;

    flag=; for(int i=p1;i>=;i--) { R[len2++]=p[i]; if(i==p2) { flag=; break; } }
    if(flag==) for(int i=n;i>=p2;i--) R[len2++]=p[i];

    for(int i=;i<len2/;i++) swap(R[i],R[len2-i-]);
    bool fail=; for(int i=;i<len1;i++) if((LL)L[i].y*(LL)v>(LL)L[i].x*(LL)u) { fail=; break; }

    int xmax=-INF; for(int i=;i<=n;i++) xmax=max(xmax,p[i].x);
    if(xmax<=) fail=;
    if(fail==) printf("%.6lf\n",1.0*w/u);
    else
    {
        double ans=; int pre=;
        for(int i=;i<len2;i++)
        {
            ans=ans+1.0*(R[i].y-pre)/u; pre=R[i].y;
            ans=max(ans,1.0*R[i].x/v);
        }
        ans=ans+1.0*(w-pre)/u;
        printf("%.6lf\n",ans);
    }
    return ;
}