Hdu 2513 区间DP

Cake slicing

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 149    Accepted Submission(s): 86

Problem Description

A rectangular cake with a grid of m*n unit squares on its top needs to be sliced into pieces. Several cherries are scattered on the top of the cake with at most one cherry on a unit square. The slicing should follow the rules below:
1.  each piece is rectangular or square;
2.  each cutting edge is straight and along a grid line;
3.  each piece has only one cherry on it;
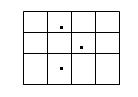
4.  each cut must split the cake you currently cut two separate parts

For example, assume that the cake has a grid of 3*4 unit squares on its top, and there are three cherries on the top, as shown in the figure below.

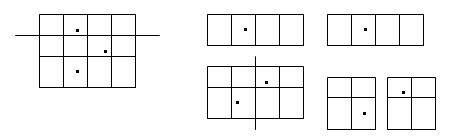
One allowable slicing is as follows.

For this way of slicing , the total length of the cutting edges is 2+4=6.
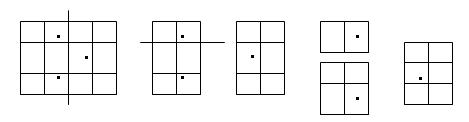
Another way of slicing is 

In this case, the total length of the cutting edges is 3+2=5.

Give the shape of the cake and the scatter of the cherries , you are supposed to find
out the least total length of the cutting edges.

Input

The input file contains multiple test cases. For each test case:
The first line contains three integers , n, m and k (1≤n, m≤20), where n*m is the size of the unit square with a cherry on it . The two integers show respectively the row number and the column number of the unit square in the grid .
All integers in each line should be separated by blanks.

Output

Output an integer indicating the least total length of the cutting edges.

Sample Input

3 4 3
1 2
2 3
3 2

Sample Output

Case 1: 5

Accepted Code:

 /*************************************************************************
     > File Name: 2513.cpp
     > Author: Stomach_ache
     > Mail: sudaweitong@gmail.com
     > Created Time: 2014年07月10日 星期四 18时34分23秒
     > Propose:
  ************************************************************************/
 
 #include <cmath>
 #include <string>
 #include <cstdio>
 #include <fstream>
 #include <cstring>
 #include <iostream>
 #include <algorithm>
 using namespace std;
 
 #define min(x, y) ((x) < (y) ? (x) : (y))
 
 int n, m, cherry;
 int dp[][][][];
 int a[][], sum[][];
 
 int DP(int sx, int ex, int sy, int ey) {
       if (dp[sx][ex][sy][ey] != -) return dp[sx][ex][sy][ey];
     int cnt = ;
     for (int i = sx; i <= ex; i++) for (int j = sy; j <= ey; j++)
           if (a[i][j]) cnt++;
     if (cnt == ) return dp[sx][ex][sy][ey] = ;
 
     int ans = 0x3f3f3f3f;
     for (int i = sx; i < ex; i++) {
           int tmp = sum[i][ey] - sum[i][sy-] - sum[sx-][ey] + sum[sx-][sy-];
           if (tmp) {
               ans = min(ans, DP(sx, i, sy, ey)+DP(i+, ex, sy, ey)+ey-sy+);
         }
     }
     for (int i = sy; i < ey; i++) {
           int tmp = sum[ex][i] - sum[ex][sy-] - sum[sx-][i] + sum[sx-][sy-];
         if (tmp) {
               ans = min(ans, DP(sx, ex, sy, i)+DP(sx, ex, i+, ey)+ex-sx+);
         }
     }
     return dp[sx][ex][sy][ey] = ans;
 }
 
 int main(void) {
       int c = ;
       while(~scanf("%d %d %d", &n, &m, &cherry)) {
           memset(a, , sizeof(a));
           for (int i = ; i < cherry; i++) {
               int x, y;
             scanf("%d %d", &x, &y);
             a[x][y] = ;
         }
         memset(sum, , sizeof(sum));
         for (int i = ; i <= n; i++) {
               for (int j = ; j <= m; j++) {
                   sum[i][j] = sum[i-][j] + sum[i][j-] - sum[i-][j-];
                   if (a[i][j]) sum[i][j]++;
             }
         }
         memset(dp, -, sizeof(dp));
         DP(, n, , m);
         printf("Case %d: %d\n", c++, dp[][n][][m]);
     }
 
     return ;
 }