第二十八篇 玩转数据结构——堆（Heap）和有优先队列(Priority Queue)

 

 

 

1.. 优先队列（Priority Queue）

• 优先队列与普通队列的区别：普通队列遵循先进先出的原则；优先队列的出队顺序与入队顺序无关，与优先级相关。
• 优先队列可以使用队列的接口，只是在实现接口时，与普通队列有两处区别，一处在于优先队列出队的元素应该是优先级最高的元素，另一处在于队首元素也是优先级最高的元素。
• 优先队列也可以使用不同的底层实现，不同底层实现的时间复杂度如下：
• 
• 从上图可以看出，使用"堆"这种数据结构来实现优先队列是比较高效的。

2.. 二叉堆（Binary Heap）

• 二叉堆就是一棵满足特殊性质的二叉树
• 首先，二叉堆是一棵完全二叉树，"完全二叉树"，不一定是满二叉树，不满的部分一定位于整棵树的右下侧。
• 其次，堆中某个节点的值总是不大于其父节点的值（最大堆）；相应的，堆中的某个节点的值总是不小于其父节点的值（最小堆）。
• 节点值的大小与其所处的层次没有必然联系，即，最大堆中，只需保证每个节点不大于其父节点即可，至于大不大于其父节点的兄弟节点，没有任何关系。
• 可以用数组来存储二叉堆，如下图所示：
• 
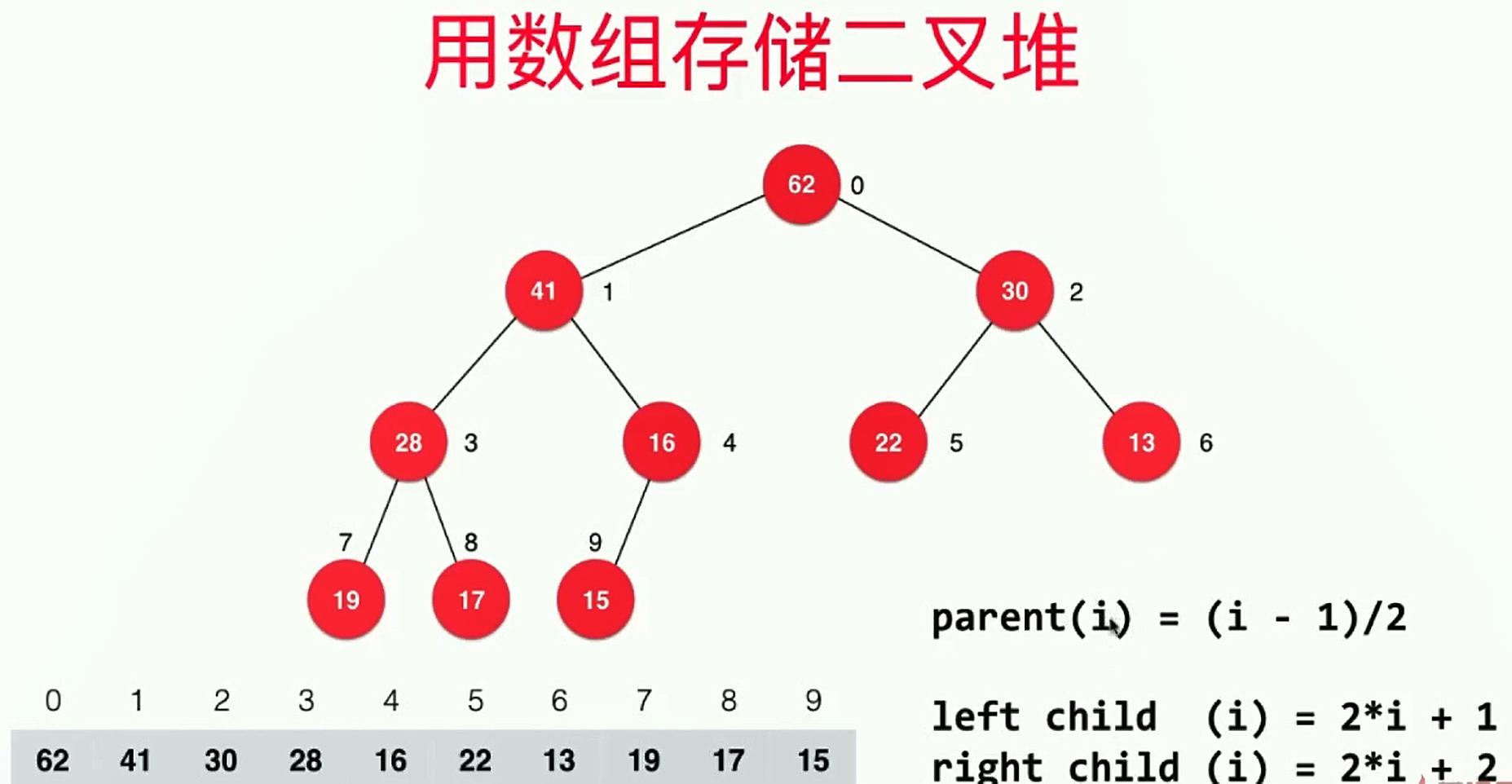
• 用动态数组实现二叉堆的业务逻辑如下：

• public class MaxHeap<E extends Comparable<E>> {
   
      private Array<E> data = new Array<>();
   
      // 构造函数
      public MaxHeap(int capacity) {
          data = new Array<>(capacity);
      }
   
      // 无参数构造函数
      public MaxHeap() {
          data = new Array<>();
      }
   
      // 接收参数为数组的构造函数
      public MaxHeap(E[] arr) {
          data = new Array<>(arr);
          for (int i = parent(arr.length - 1); i >= 0; i--) {
              SiftDown(i);
          }
      }
   
      // 实现getSize方法，返回堆中的元素个数
      public int getSize() {
          return data.getSize();
      }
   
      // 实现isEmpty方法，返回堆是否为空
      public boolean isEmpty() {
          return data.isEmpty();
      }
   
      // 返回完全二叉树的数组表示中，一个索引所表示的元素的父节点的索引
      private int parent(int index) {
          if (index == 0) {
              throw new IllegalArgumentException("Index-0 doesn't have parent.");
          }
          return (index - 1) / 2;
      }
   
      // 返回完全二叉树的数组表示中，一个索引所表示的元素的左孩子的索引
      private int leftChild(int index) {
          return index * 2 + 1;
      }
   
      // 返回完全二叉树的数组表示中，一个索引所表示的元素的右孩子的索引
      private int rightChild(int index) {
          return index * 2 + 2;
      }
   
      // 实现add方法，向堆中添加元素
      public void add(E e) {
          data.addLast(e);
          SiftUp(data.getSize() - 1);
      }
   
      // 实现元素的上浮
      private void SiftUp(int k) {
          while (k > 0 && data.get(parent(k)).compareTo(data.get(k)) < 0) {
              data.swap(k, parent(k));
              k = parent(k);
          }
      }
   
      // 实现findMax方法，查看堆中的最大元素
      public E findMax() {
          if (data.getSize() == 0) {
              throw new IllegalArgumentException("Can not findMax when heap is empty.");
          }
          return data.get(0);
      }
   
      // 实现extractMax方法，取出堆中的最大元素
      public E extractMax() {
          E ret = findMax();
          data.swap(0, data.getSize() - 1);
          data.removeLast();
          SiftDown(0);
          return ret;
      }
   
      // 实现元素的下沉
      private void SiftDown(int k) {
          while (leftChild(k) < data.getSize()) {
              int j = leftChild(k);
              if (j + 1 < data.getSize() && data.get(j + 1).compareTo(data.get(j)) > 0) {
                  j = rightChild(k);
                  // data[j]是leftChild和rightChild中的对大值
              }
              if (data.get(k).compareTo(data.get(j)) >= 0) {
                  break;
              } else {
                  data.swap(k, j);
                  k = j;
              }
          }
      }
   
      // 实现replace方法，取出堆中的最大元素，并替换为元素e
      public E replace(E e) {
          E ret = findMax();
          data.set(0, e);
          SiftDown(0);
          return ret;
      }
  }

• 测试用动态数组实现的二叉堆

• import java.util.Random;
   
  public class Main {
   
      public static void main(String[] args) {
   
          int n = 1000000;
          MaxHeap<Integer> maxHeap = new MaxHeap<>();
          Random random = new Random();
          for (int i = 0; i < n; i++) {
              maxHeap.add(random.nextInt(Integer.MAX_VALUE));
          }
   
          int[] arr = new int[n];
          for (int i = 0; i < n; i++) {
              arr[i] = maxHeap.extractMax();
          }
   
          for (int i = 1; i < n; i++) {
              if (arr[i - 1] < arr[i]) {
                  throw new IllegalArgumentException("Error");
              }
          }
   
          System.out.println("Test MaxHeap completed.");
      }
  }

• 二叉堆的时间复杂度分析
• 
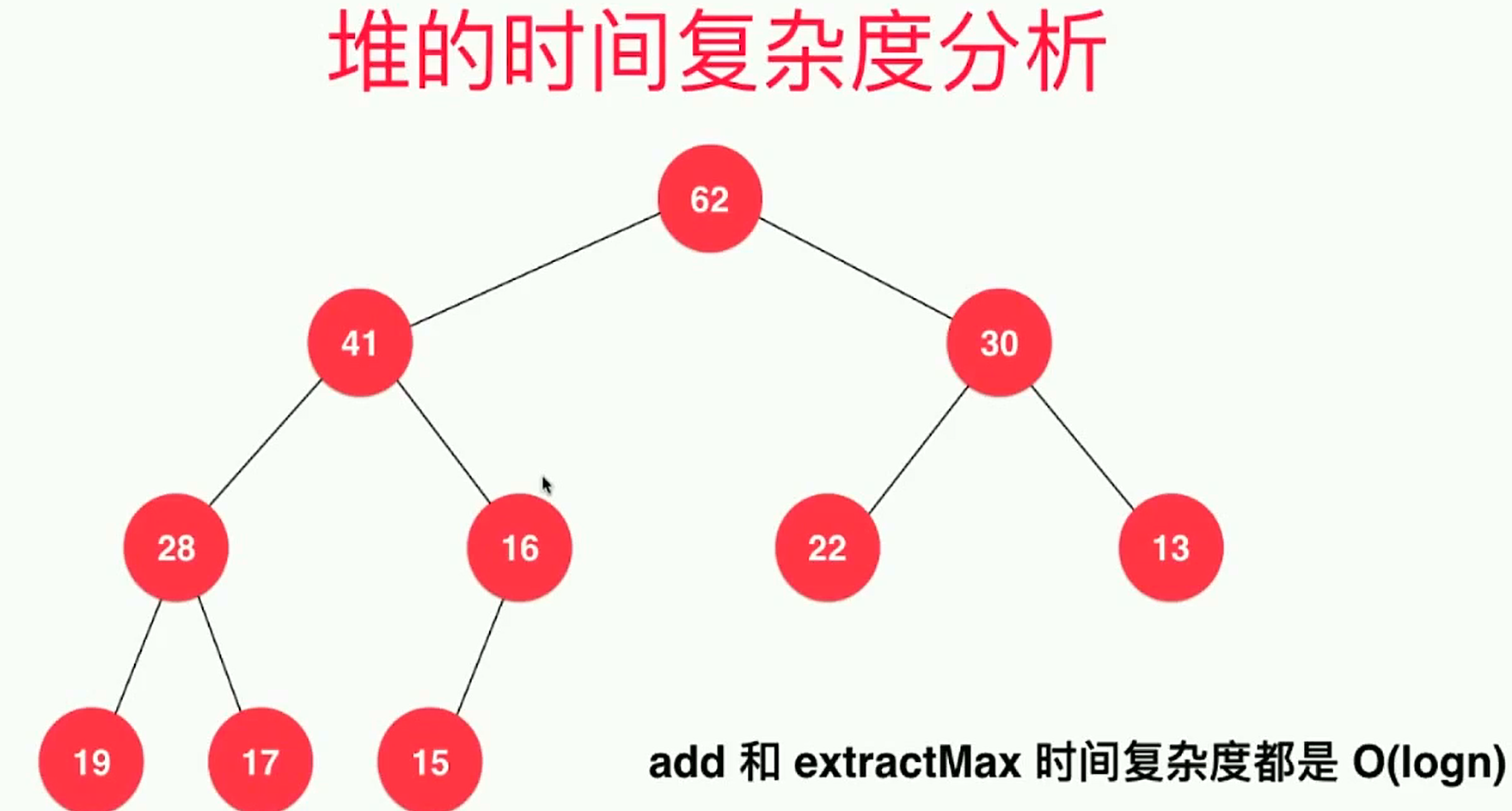
• 由于堆是一棵完全二叉树，所以堆不会退化成链表。

3.. 用最大堆实现一个优先队列（Priority Queue）

• 实现优先队列的业务逻辑如下：

• public class PriorityQueue<E extends Comparable<E>> implements Queue<E> {
   
      private MaxHeap<E> maxHeap;
   
      // 构造函数
      public PriorityQueue() {
          maxHeap = new MaxHeap<>();
      }
   
      // 实现getSize方法
      @Override
      public int getSize() {
          return maxHeap.getSize();
      }
   
      // 实现isEmpty方法
      @Override
      public boolean isEmpty() {
          return maxHeap.isEmpty();
      }
   
      // 实现getFront方法
      @Override
      public E getFront() {
          return maxHeap.findMax();
      }
   
      // 实现enqueue方法
      @Override
      public void enqueue(E e) {
          maxHeap.add(e);
      }
   
      // 实现dequeue方法
      @Override
      public E dequeue() {
          return maxHeap.extractMax();
      }
  }

4.. 优先队列的应用：从N个元素中，选出前M个

• 解决方案：使用优先队列，维护当前的M个元素，然后不断更新元素，直到扫描完所有N个元素。
• 需要使用"最小堆"来进行底层的实现，因为最终获取的是前M个元素，通过最小堆的extractMin方法，可以不断的剔除堆中的最小元素
• 也可以使用最大堆来实现，我们只要规定元素越小，优先级越高。
• 使用最小堆实现的业务逻辑如下：

• import java.util.List;
  import java.util.PriorityQueue;
  import java.util.TreeMap;
   
  public class Solution2 {
   
      private class Freq implements Comparable<Freq> {
   
          public int e, freq;
   
          public Freq(int e, int freq) {
              this.e = e;
              this.freq = freq;
          }
   
          public int compareTo(Freq another) {
              if (this.freq < another.freq)
                  return -1;
              else if (this.freq > another.freq)
                  return 1;
              else
                  return 0;
          }
      }
   
      public List<Integer> topKFrequent(int[] nums, int k) {
   
          TreeMap<Integer, Integer> map = new TreeMap<>();
          for (int num : nums) {
              if (map.containsKey(num))
                  map.put(num, map.get(num) + 1);
              else
                  map.put(num, 1);
          }
   
          PriorityQueue<Freq> pq = new PriorityQueue<>();
          for (int key : map.keySet()) {
              if (pq.size() < k)
                  pq.add(new Freq(key, map.get(key)));
              else if (map.get(key) > pq.peek().freq) {
                  pq.remove();
                  pq.add(new Freq(key, map.get(key)));
              }
          }
   
          LinkedList<Integer> res = new LinkedList<>();
          while (!pq.isEmpty())
              res.add(pq.remove().e);
          return res;
      }
  }