Weka算法Classifier-tree-J48源代码分析（一个）基本数据结构和算法

大约一年，我没有照顾的博客，再次拿起笔不知从何写上，想来想去手从最近使用Weka要正确书写。

Weka为一个Java基础上的机器学习工具。上手简单，并提供图形化界面。提供如分类、聚类、频繁项挖掘等工具。本篇文章主要写一下分类器算法中的J48算法及事实上现。

一、算法

J48是基于C4.5实现的决策树算法。对于C4.5算法相关资料太多了。笔者在这里转载一部分（来源：http://blog.csdn.net/zjd950131/article/details/8027081）

C4.5是一系列用在机器学习和数据挖掘的分类问题中的算法。

它的目标是监督学习：给定一个数据集，当中的每个元组都能用一组属性值来描写叙述，每个元组属于一个相互排斥的类别中的某一类。C4.5的目标是通过学习。找到一个从属性值到类别的映射关系，而且这个映射能用于对新的类别未知的实体进行分类。

C4.5由J.Ross Quinlan在ID3的基础上提出的。ID3算法用来构造决策树。决策树是一种类似流程图的树结构，当中每一个内部节点（非树叶节点）表示在一个属性上的測试，每一个分枝代表一个測试输出。而每一个树叶节点存放一个类标号。一旦建立好了决策树。对于一个未给定类标号的元组，跟踪一条有根节点到叶节点的路径，该叶节点就存放着该元组的预測。决策树的优势在于不须要不论什么领域知识或參数设置。适合于探測性的知识发现。

从ID3算法中衍生出了C4.5和CART两种算法。这两种算法在数据挖掘中都很重要。下图就是一棵典型的C4.5算法对数据集产生的决策树。

数据集如图1所看到的。它表示的是天气情况与去不去打高尔夫球之间的关系。

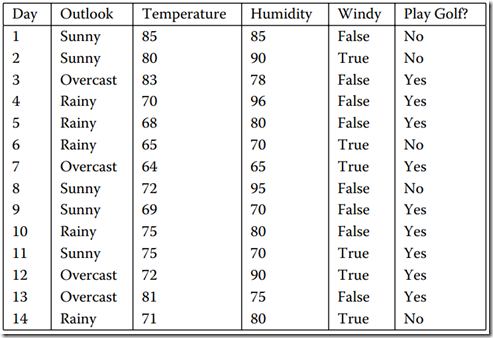
图1  数据集

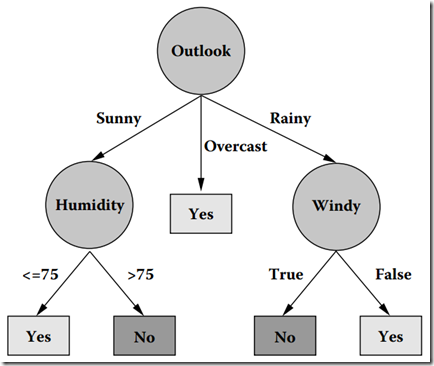
图2   在数据集上通过C4.5生成的决策树

算法描写叙述

C4.5并不一个算法，而是一组算法—C4.5，非剪枝C4.5和C4.5规则。下图中的算法将给出C4.5的基本工作流程：

图3  C4.5算法流程

我们可能有疑问，一个元组本身有非常多属性，我们怎么知道首先要对哪个属性进行推断，接下来要对哪个属性进行推断？换句话说，在图2中，我们怎么知道第一个要測试的属性是Outlook，而不是Windy？事实上，能回答这些问题的一个概念就是属性选择度量。

属性选择度量

属性选择度量又称分裂规则，由于它们决定给定节点上的元组怎样分裂。属性选择度量提供了每一个属性描写叙述给定训练元组的秩评定。具有最好度量得分的属性被选作给定元组的分裂属性。眼下比較流行的属性选择度量有--信息增益、增益率和Gini指标。

先做一些如果，设D是类标记元组训练集，类标号属性具有m个不同值，m个不同类Ci(i=1,2,…，m)，CiD是D中Ci类的元组的集合，|D|和|CiD|各自是D和CiD中的元组个数。

（1）信息增益

信息增益实际上是ID3算法中用来进行属性选择度量的。它选择具有最高信息增益的属性来作为节点N的分裂属性。该属性使结果划分中的元组分类所需信息量最小。对D中的元组分类所需的期望信息为下式：

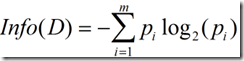 （1）

Info(D)又称为熵。

如今假定依照属性A划分D中的元组，且属性A将D划分成v个不同的类。

在该划分之后，为了得到准确的分类还须要的信息由以下的式子度量：

      
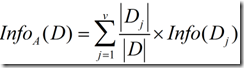
（2）

信息增益定义为原来的信息需求（即仅基于类比例）与新需求（即对A划分之后得到的）之间的差。即

      
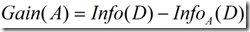
（3）

我想非常多人看到这个地方都认为不是非常好理解，所以我自己的研究了文献中关于这一块的描写叙述，也对照了上面的三个公式。以下说说我自己的理解。

一般说来。对于一个具有多个属性的元组，用一个属性就将它们全然分开差点儿不可能，否则的话。决策树的深度就仅仅能是2了。从这里能够看出，一旦我们选择一个属性A，如果将元组分成了两个部分A1和A2，因为A1和A2还能够用其他属性接着再分，所以又引出一个新的问题：接下来我们要选择哪个属性来分类？对D中元组分类所需的期望信息是Info(D)
,那么同理，当我们通过A将D划分成v个子集Dj(j=1,2,…,v)之后。我们要对Dj的元组进行分类，须要的期望信息就是Info(Dj),而一共同拥有v个类。所以对v个集合再分类，须要的信息就是公式（2）了。由此可知，假设公式（2）越小，是不是意味着我们接下来对A分出来的几个集合再进行分类所须要的信息就越小？而对于给定的训练集，实际上Info(D)已经固定了，所以选择信息增益最大的属性作为分裂点。

可是。使用信息增益的话事实上是有一个缺点，那就是它偏向于具有大量值的属性。

什么意思呢？就是说在训练集中。某个属性所取的不同值的个数越多。那么越有可能拿它来作为分裂属性。

比如一个训练集中有10个元组，对于某一个属相A，它分别取1-10这十个数，假设对A进行分裂将会分成10个类。那么对于每个类Info(Dj)=0，从而式（2）为0，该属性划分所得到的信息增益（3）最大，可是非常显然，这样的划分没有意义。

（2）信息增益率

正是基于此，ID3后面的C4.5採用了信息增益率这样一个概念。信息增益率使用“分裂信息”值将信息增益规范化。分类信息类似于Info(D)，定义例如以下：

   
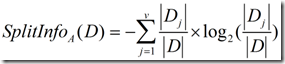
（4）

这个值表示通过将训练数据集D划分成相应于属性A測试的v个输出的v个划分产生的信息。信息增益率定义：

        
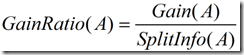
（5）

选择具有最大增益率的属性作为分裂属性。

二、算法说明

（1）我们是要构造一个决策树。非常自然地，树的每一层代表一个属性的取值，最后的叶子节点指向划分的类。

如图二所看到的。

（2）因此非常自然的问题就是怎样在每一层选择合适的节点去构造这个树使这个树的结构尽可能最优，也就是查找路径尽可能的短。

（3）因此最关键的问题就是怎样在每一层，从剩下的还没被分配的节点中找出最合适的分裂节点。

（4）当中ID3算法选择最优节点的方式是：选出信息增益增益最高的属性。信息增益能够简单理解成使用某个属性划分后，不确定性的降低量。

（5）而C4.5算法做了一个改进。使用信息增益率最高的属性，这样做的优点是，能够避免树过宽。

（6）构建好了树之后还要进行一些剪枝的操作，当然这个不体如今算法主流行里。也没有做强求。但能够注意一下Weka是怎样实现的。

三、算法中用到的主要数据结构

（1）Instances对象

一个Instances代表一张表。能够相应一个arff文件或者是一个csv文件，通过Instances对象能够取某一列的均值方差等，主要就是若干行记录的一个封装。

（2）Instance

一个Instance代表一行记录。换言之中的一个个Instances的数据包括多个Instance。每一个Instance会有一个特殊的列ClassIndex，该列值代表该Instance属于哪一类。详细来说就是图一里面的Golf。

（3）Classifier接口

Weka中每个分类器都继承与这个接口（尽管从意义上来说是个接口但事实上是个子类）。该接口提供一个buildClassifier方法传入一个Instances对象用于训练。还有classifyInstance方法用于传入一个Instance来推断其属于哪个类。

（4）J48

分类器主类，实现了Classifier接口。

（5）ClassifierTree接口

代表树中的一个节点。维护和组成树的结构。当中J48用到的是C45PruneableClassifierTree和PruneableClassifierTree。

（6）ModelSelection接口

该接口负责推断和选取最优的属性。然后依据该属性将不同的Instance放到不同的subset中，ClassifierTree接口使用ModelSelection来生成树的结构。

这样的抽象方式还是非常值得学习的。J48中用到的该接口的实现有BinC45ModelSelection和C45ModelSelection，通过名字大概也能看出来前一个是生成二叉树（即每一个节点仅仅含有是否两种回答）。后一个是生成标准的C45树。

未完待续。。

。。。

。

版权声明：本文博客原创文章，博客，未经同意，不得转载。