HDU 6363

题意略。

思路：

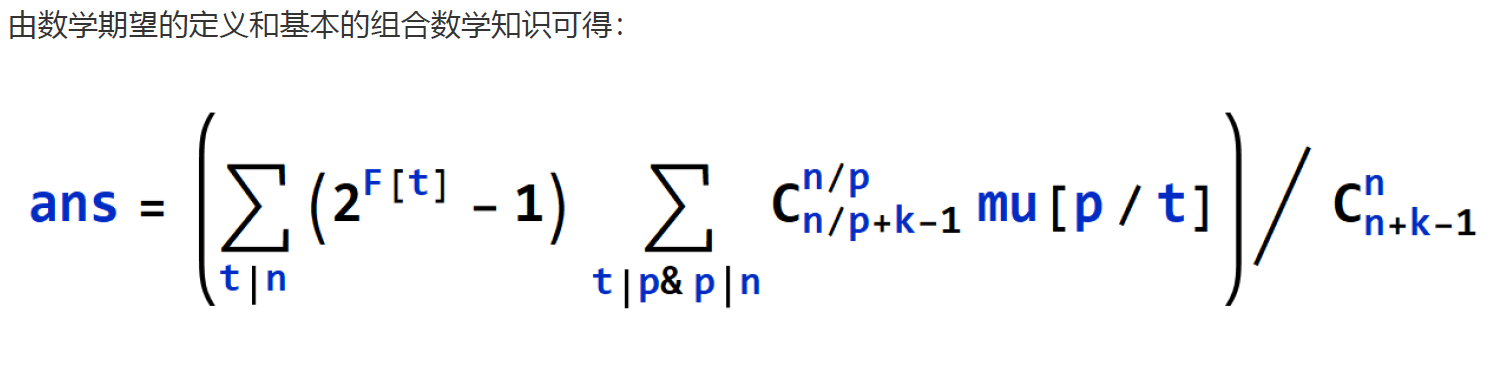
这里有两个结论需要注意：

1.gcd(a ^ x - 1，a ^ y - 1) = a ^ gcd(x，y) - 1

2.gcd(fib[x]，fib[y]) = fib[gcd(x，y)]

详见代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn = 1e6 + ;
const LL mod = 1e9 + ;
const LL mm = 1e9 + ;

LL inv[maxn *  + ],fac[maxn *  + ];
bool check[maxn];
LL prime[maxn],mu[maxn],f[maxn],n,k;

LL exgcd(LL a,LL b,LL& x,LL& y){
    if(a ==  && b == ) return -;
    if(b == ){
        x = ,y = ;
        return a;
    }
    LL d = exgcd(b,a % b,y,x);
    y -= a / b * x;
    return d;
}
LL rev(LL a,LL n){
    LL x,y;
    LL d = exgcd(a,n,x,y);
    return (x % n + n) % n;
}
void init_inv(){
    fac[] = ;
    for(LL i = ;i <  * maxn;++i) fac[i] = fac[i - ] * i % mod;
    inv[ * maxn - ] = rev(fac[ * maxn - ],mod);
    for(LL i =  * maxn - ;i >= ;--i){
        inv[i] = (i + ) * inv[i + ] % mod;
    }
}
LL C(LL a,LL b){
    LL m = a,n = b;
    return ((fac[n] * inv[m]) % mod * inv[n - m]) % mod;
}
void init(){
    f[] = ,f[] = ;
    for(int i = ;i < maxn;++i){
        f[i] = (f[i - ] + f[i - ]) % mm;
    }
}
void mobius(){
    memset(check,false,sizeof(check));
    mu[] = ;
    int tot = ;
    for(LL i = ;i < maxn;++i){
        if(!check[i]){
            prime[tot++] = i;
            mu[i] = -;
        }
        for(int j = ;j < tot;++j){
            if(i * prime[j] > maxn) break;
            check[i * prime[j]] = true;
            if(i % prime[j] == ){
                mu[i * prime[j]] = ;
                break;
            }
            else mu[i * prime[j]] = -mu[i];
        }
    }
}
LL qmod(LL a,LL n){
    LL ret = ;
    while(n){
        if(n & ) ret = ret * a % mod;
        a = a * a % mod;
        n = n>>;
    }
    return ret;
}

int main(){
    init_inv();
    mobius();
    init();
    int T;
    scanf("%d",&T);
    while(T--){
        scanf("%lld%lld",&n,&k);
        LL denominator = C(n,n + k - );
        denominator = rev(denominator,mod);
        LL ans = ;
        for(int i = ;i <= n;++i){
            if(n % i) continue;
            LL div = i;
            LL contri = (qmod(,f[div]) -  + mod) % mod;
            LL cnt = ;
            for(LL j = div;j <= n;j += div){
                if(n % j) continue;
                LL d = j;
                cnt += mu[d / i] * C(n / d,n / d + k - ) % mod;
                cnt = (cnt % mod + mod) % mod;
            }
            ans += contri * cnt % mod;
            ans %= mod;
        }
        ans = ans * denominator % mod;
        printf("%lld\n",ans);
    }
    return ;
}