【LeetCode】334#递增的三元子序列

题目描述

给定一个未排序的数组，判断这个数组中是否存在长度为 3 的递增子序列。

数学表达式如下:

如果存在这样的 i, j, k, 且满足 0 ≤ i < j < k ≤ n-1，

使得 arr[i] < arr[j] < arr[k] ，返回 true ; 否则返回 false 。

说明: 要求算法的时间复杂度为 O(n)，空间复杂度为 O(1) 。

示例 1:

输入: [1,2,3,4,5]
输出: true

示例 2:

输入: [5,4,3,2,1]
输出: false

---

解题思路

1、暴力破解

使用三层循环，先找到二元上升序列，再在二元上升序列的基础上，找三元上升序列，时间复杂度为O(N^3)。

源代码

public boolean increasingTriplet (int[] nums) {
    if (nums.length < 3) return false;
    for (int i = 0; i < nums.length-2; i++) {
        for (int j = i+1; j < nums.length - 1; j++) {
            if (nums[j] > nums[i]) {
                for (int k = j+1; k < nums.length; k++) {
                    if (nums[k] > nums[j]) {
                        return true;
                    }
                }
            }
        }
    }
    return false;
}

2、一次遍历法

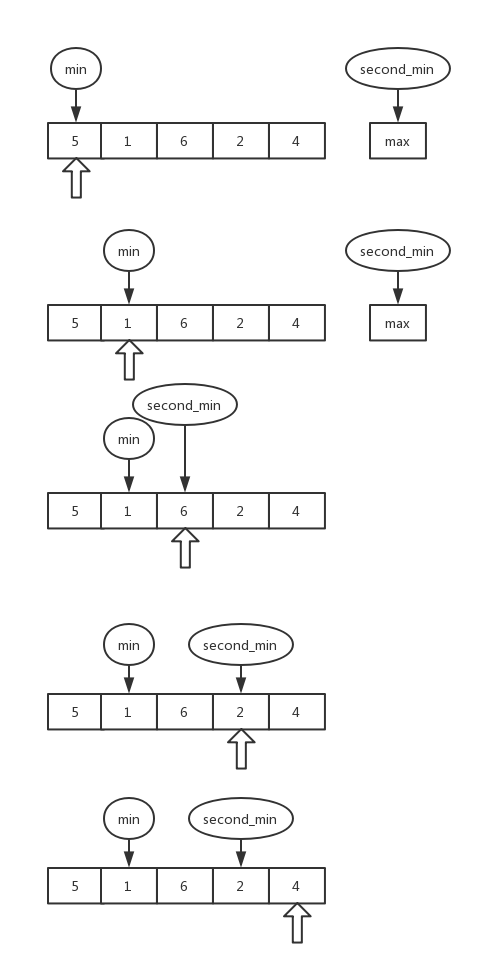
维护两个常量：min和second_min，对数组进行遍历。

其中，min表示遍历到当前位置最小的元素，second_min表示从min的位置开始一直到当前位置的第二小元素（也就是比min大的元素中最小的那一个）。

确定这两个元素后，再在后续的元素中找有没有比second_min大的元素，如果有，就表示存在递增的三元子序列。

这样只需要遍历一次数组，时间复杂度为O(N)。

示意图

源代码

public boolean increasingTriplet (int[] nums) {
    int min = Integer.MAX_VALUE;
    int second_min = Integer.MAX_VALUE;
    for (int num : nums) {
        if (num<=min) min = num;
        else if (num < second_min) second_min = num;
        else if (num > second_min) return true;
    }
    return false;
}

心得体会

一次遍历法的巧妙就在于设置了两个变量（或者叫指针）来保存递增二元子序列，并实时更新，避免了许多重复的判断。