[动态规划]高数Umaru系列（9）——哈士奇(背包问题)

高数Umaru系列（9）——哈士奇

http://acm.sdut.edu.cn/onlinejudge2/index.php/Home/Index/problemdetail/pid/3358.html

Time Limit: 1000 ms Memory Limit: 65536 KiB

 

Problem Description

由于高数巨养的喵星人太傲娇了，要天天吃新鲜猫粮而且还经常欺负高数巨，所以高数巨决定买几条哈士奇尝尝鲜。这天高数巨来到了二手狗市场买哈士奇，高数巨看完了所有的哈士奇，记下了每条哈士奇的价格，并根据对它们的好感程度给它们每只都赋予了一个萌值。高数现在手里有X元，她想通过购买若干条哈士奇来获得尽可能多的萌值。现在给定高数巨手里的钱X以及N条哈士奇的价格和萌值，求高数巨最多可获得多少萌值

Input

多组输入。

对于每组输入，第一行有两个整数N，X（1 < = N < = 100，1 < = X < = 1000），分别表示哈士奇的数量和高数巨的钱数

接下来的N行每行有两个整数Pi，Mi（1 < = Pi,Mi < = 100），分别表示第i条哈士奇的价格和萌值

Output

对于每组数据，输出一个整数，表示高数巨最多可以获得的萌值，每组输出占一行

Sample Input

2 100
50 20
60 40
3 100
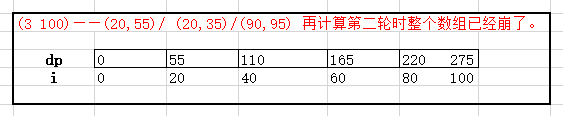
20 55
20 35
90 95
1 10
20 50

Sample Output

40
95
0

Hint

Source

Shannon

---

算法思路：

　　这道题很明显是一个背包问题，即“在有限的背包容量下，如何选择价值总和最高的物品”。

　　关于该问题有很多比较详细的解答，该算法的核心“面对一个物品i，是否要将该物品放进背包里”。

　　对于理解这个算法，我们要明确：每个物品都是有重量的，会有沉默成本，放进物品i必定会承担不放进物品j的成本，所以比较的是获益和成本，当获益大于成本，那么就将这件物品放进背包里。

 

核心代码：

 for (int i = ; i < n; i++) { // 存储的物品个数
     for (int k = v; k >= w[i]; k--) { // 从所需要的重量到当前重量
         dp[k] = max(dp[k], dp[k - w[i]] + p[i]);
     }
 }

代码解读：

1. 有很多人采用二维数组dp[i][j]静态地更新来解决背包问题，使用二维数组更加直观，但是不普遍。
2. 采用一维数组动态更新看起来比较难理解，但使用范围比较广。(比如，硬币问题中，三重循环，也可以采用一维数组来解决，但如果使用二维的话，对应地应该上升到三维)

难点： "k:v->w[i]，依次递减"，这可能比较难以理解，在我们默认从小到大，而这里，必须从大到小，否则就是错误。

难点解答：

　　我们产生上述问题，本质就是对dp[]数组在某一时间其存储的值的不理解。

　　对于每一次更新开始，dp[]存储着的是“放入这个物品之前的最优解”，而我们比较的是 dp[k] 与 dp[k - w[i]] + p[i]，其中 dp[k-w[i]]是之前的最优解。

　　因为一定存在 k > k-w[i]，如果从小到大，则一定会先与dp[k]更新dp[k-w[i]]，这就会导致比较错误。此时dp[k-w[i]]已经变为"将该商品放入之后的最优价值"，在这价值基础之上，在加p[i]，其价值大概率会比 dp[k] 高，而更新，这样，越来越大，完全背离了我们实际的意思。

　　因此，必须从后往前，因为前面存储着的是过去的值(不放第i件物品时的值)进行比较；但从小到大，该值就更新为现在的值，已经放入，但我们自认为其并没有放入，从而再放入多计算一次，这样又有什么意思呢。

 

　　当采用从小到大时第二轮数组的结果：

　　

---

源代码：

 #include "pch.h"
 #include <iostream>
 #include <algorithm>
 
 using namespace std;
 
 int main() {
     int n, v;
     int w[], p[];
     while (~scanf_s("%d%d", &n, &v)) {
         for (int i = ; i < n; i++) {
             // w 重量  | p 价值
             scanf_s("%d%d", &w[i], &p[i]);
         }
         // 清空数组
         int dp[] = {  };
         for (int i = ; i < n; i++) { // 存储的物品个数
             for (int k = v; k >= w[i]; k--) { // 从所需要的重量到当前重量
                 dp[k] = max(dp[k], dp[k - w[i]] + p[i]);
             }
         }
         printf("%d\n", dp[v]);
     }
 }