POJ 1185 炮兵阵地 （状态压缩DP）

题目链接

Description

司令部的将军们打算在NM的网格地图上部署他们的炮兵部队。一个NM的地图由N行M列组成，地图的每一格可能是山地（用"H" 表示），也可能是平原（用"P"表示），如下图。在每一格平原地形上最多可以布置一支炮兵部队（山地上不能够部署炮兵部队）；一支炮兵部队在地图上的攻击范围如图中黑色区域所示：

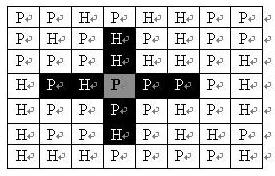
如果在地图中的灰色所标识的平原上部署一支炮兵部队，则图中的黑色的网格表示它能够攻击到的区域：沿横向左右各两格，沿纵向上下各两格。图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。

现在，将军们规划如何部署炮兵部队，在防止误伤的前提下（保证任何两支炮兵部队之间不能互相攻击，即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内），在整个地图区域内最多能够摆放多少我军的炮兵部队。

Input

第一行包含两个由空格分割开的正整数，分别表示N和M；

接下来的N行，每一行含有连续的M个字符('P'或者'H')，中间没有空格。按顺序表示地图中每一行的数据。N <= 100；M <= 10。

Output

仅一行，包含一个整数K，表示最多能摆放的炮兵部队的数量。

Sample Input

5 4

PHPP

PPHH

PPPP

PHPP

PHHP

Sample Output

6

分析：

实现需要考虑到一点就是，我们在进行放炮兵的时候，肯定是有一定的方向性的，所以在判断当前这个点能不能放置炮兵的时候，我们只需要考虑它的上一行和上上一行炮兵放置的状态就可以了。

当然还有一点就是如果当前这个点放置了炮兵的话，为了防止本行内的炮兵之间相互攻击，那么下一个需要判断的能不能放置炮兵的地方就是它本身往右走第三个位置，可以直接跳过去；如果当前这个位置没有放置炮兵的话，就得一个位置一个位置的挨着进行判断。

用0和1来表示一个位置有没有放炮兵，1表示放了，0表示没有，这样每一行的放置炮兵的状态都可以用二进制数来表示，二进制数之间进行与运算，就可以判断出来这一行的当前位置如果放置炮兵的话会不会与之前的情况产生冲突。

代码：

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <string>
#include <queue>
#include <algorithm>
#include <map>
#include <cmath>
#include <iomanip>
#define INF 99999999
typedef long long LL;
using namespace std;

const int MAX=100+10;
int n,m,lastsize,lastlastsize,nowsize;  //nowsize当前行的方案数，lastsize上一行的方案数，lastlastsize上上一行的方案数
int last[MAX],lastlast[MAX],now[MAX];  // now[i]第i行的方案......
int num[MAX],dp[MAX][MAX],temp[MAX][MAX];  //dp[i][j]  i代表当前行 j代表上一行
//temp[j][t] j上一行 t上上行
char Map[MAX][MAX];

void dfs(int id,int k,int p,int sum)
{
    if(k>=m)
    {
        now[++nowsize]=p;
        num[nowsize]=sum;
        return;
    }
    if(Map[id][k] == 'P')   				//找到可安放炮兵的位置
        dfs(id,k+3,p|(1<<k),sum+1);
    dfs(id,k+1,p,sum);
}

void DP()
{
    for(int k=1; k<=n; ++k)
    {
        memset(now,0,sizeof now);
        nowsize=0;
        dfs(k,0,0,0);
        for(int i=1; i<=nowsize; ++i)
            for(int j=1; j<=lastsize; ++j)
                dp[i][j]=0;
        for(int i=1; i<=nowsize; ++i) //本行选择第几个方案
        {
            for(int j=1; j<=lastsize; ++j) //上一行选择第几个方案
            {
                for(int t=1; t<=lastlastsize; ++t) //上上行选择第几个方案
                {
                    if(now[i] & last[j])
                        continue;//与上一行j方案不能共存
                    if(now[i] & lastlast[t])
                        continue;//与上上行t方案不能共存
                    if(dp[i][j]<temp[j][t]+num[i])
                        dp[i][j]=temp[j][t]+num[i];
                }
            }
        }
        for(int i=1; i<=nowsize; ++i)     //将当前状态赋给上一次的， 进行下次操作
            for(int j=1; j<=lastsize; ++j)
                temp[i][j]=dp[i][j];

        for(int i=1; i<=lastsize; ++i)
            lastlast[i]=last[i];
        lastlastsize=lastsize;

        for(int i=1; i<=nowsize; ++i)
            last[i]=now[i];
        lastsize=nowsize;
    }
}

int main()
{
    while(~scanf("%d%d",&n,&m))
    {
        for(int i=1; i<=n; ++i)scanf("%s",Map[i]);
        last[1]=lastlast[1]=temp[1][1]=0;
        lastsize=lastlastsize=1;
        DP();
        int sum=0;
        for(int i=1; i<=lastsize; ++i)    //遍历temp（也就相当于是dp）值 找到其中最大的sum值
        {
            for(int j=1; j<=lastlastsize; ++j)
            {
                if(temp[i][j]>sum)
                    sum=temp[i][j];
            }
        }
        printf("%d\n",sum);
    }
    return 0;
}