学习笔记-canny边缘检测

Canny边缘检测

---

声明：阅读本文需要了解线性代数里面的点乘（图像卷积的原理），高等数学里的二元函数的梯度，极大值定义，了解概率论里的二维高斯分布

1.canny边缘检测原理和简介

2.实现步骤

3.总结

一、 Canny边缘检测算法的发展历史

　　Canny算子是28岁的John Canny在1986年提出的，该文章发表在PAMI顶级期刊(1986. A computational approach to edge detection. IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 8, 1986, pp. 679-698)。现在老大爷目前（61岁）在加州伯克利做machine learning,主页(http://www.cs.berkeley.edu/~jfc/)，大爷就是大爷。

　　边缘检测是从图像中提取有用的结构信息的一种技术，如果学过信息论就会知道，一面充满花纹的墙要比一面白墙的信息量大很多，没学过也没关系，直观上也能理解：充满花纹的图像要比单色图像信息更丰富。为什么要检测边缘?因为我们需要计算机自动的提取图像的底层（纹理等）或者高层（时间地点人物等）的信息，边缘可以说是最直观、最容易发现的一种信息了。Canny提出了一个对于边缘检测算法的评价标准，包括：

1)        以低的错误率检测边缘，也即意味着需要尽可能准确的捕获图像中尽可能多的边缘。

2)        检测到的边缘应精确定位在真实边缘的中心。

3)        图像中给定的边缘应只被标记一次，并且在可能的情况下，图像的噪声不应产生假的边缘。

　　简单来说就是，检测算法要做到：边缘要全，位置要准，抵抗噪声的能力要强。

　　接下来介绍最经典的canny边缘检测算法，很多边缘检测算法都是在此基础上进行改进的，学习它有利于一通百通。

二、实现步骤

　　step1：高斯平滑滤波

没有哪张图片是没有噪声的。————鲁迅

　　滤波是为了去除噪声，选用高斯滤波也是因为在众多噪声滤波器中，高斯表现最好（表现怎么定义的？最好好到什么程度？），你也可以试试其他滤波器如均值滤波、中值滤波等等。一个大小为(2k+1)x(2k+1)的高斯滤波器核（核一般都是奇数尺寸的）的生成方程式由下式给出：

‘

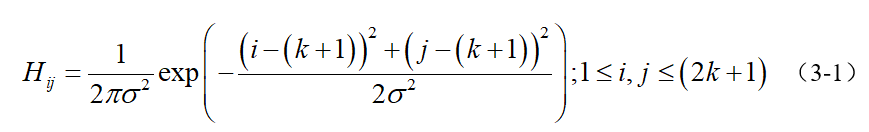　　下面是一个sigma = 1.4，尺寸为3x3的高斯卷积核的例子，注意矩阵求和值为1（归一化）：

　　举个例子：若图像中一个3x3的窗口为A，要滤波的像素点为e，则经过高斯滤波之后，像素点e的亮度值为：

　　其中*为卷积符号，sum表示矩阵中所有元素相加求和，简单说，就是滤波后的每个像素值=其原像素中心值及其相邻像素的加权求和。图像卷积是图像处理中非常重要且广泛使用的操作，一定要理解好。

其中高斯卷积核的大小将影响Canny检测器的性能。尺寸越大，去噪能力越强，因此噪声越少，但图片越模糊，canny检测算法抗噪声能力越强，但模糊的副作用也会导致定位精度不高，一般情况下，推荐尺寸5*5，3*3也行。

　　step2： 计算梯度强度和方向

边缘的最重要的特征是灰度值剧烈变化，如果把灰度值看成二元函数值，那么灰度值的变化可以用二元函数的”导数“（或者称为梯度）来描述。由于图像是离散数据，导数可以用差分值来表示，差分在实际工程中就是灰度差，说人话就是两个像素的差值。一个像素点有8邻域，那么分上下左右斜对角，因此Canny算法使用四个算子来检测图像中的水平、垂直和对角边缘。算子是以图像卷积的形式来计算梯度，比如Roberts，Prewitt，Sobel等，这里选用Sobel算子来计算二维图像在x轴和y轴的差分值（这些数字的由来？），将下面两个模板与原图进行卷积，得出x和y轴的差分值图，最后计算该点的梯度G和方向θ

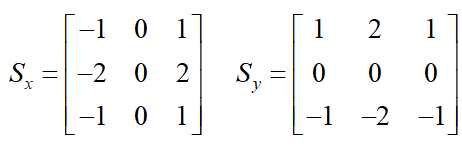
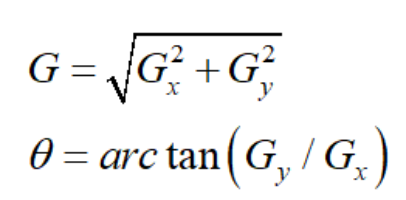
　　计算梯度的模和方向属于高等数学部分的内容，如果不理解应该补习一下数学基本功，图像处理经常会用到这个概念。

　　这部分我实现了下，首先了解opencv的二维滤波函数：dst=cv.filter2D(src, ddepth, kernel[, dst[, anchor[, delta[, borderType]]]])

　　dst：　　输出图片

　　src：　　输入图片

　　ddepth： 输出图片的深度, 详见 combinations,如果填-1，那么就跟与输入图片的格式相同。

　　kernel：   单通道、浮点精度的卷积核。

　　以下是默认参数：

　　anchor：内核的基准点(anchor)，其默认值为(-1,-1)表示位于kernel的中心位置。基准点即kernel中与进行处理的像素点重合的点。举个例子就是在上面的step1中，e=H*A得到的e是放在原像素的3*3的哪一个位置，一般来说都是放在中间位置，设置成默认值就好。

　　delta ：在储存目标图像前可选的添加到像素的值，默认值为0。（没用过）

　　borderType：像素向外逼近的方法，默认值是BORDER_DEFAULT,即对全部边界进行计算。（没用过）

　　上代码

 import cv2
 import numpy as np
 import matplotlib.pyplot as plt

 img=cv2.imread("images/luxun.png",cv2.IMREAD_GRAYSCALE)  # 读入图片
 sobel_x = np.array([[-1, 0, 1],[-2,0,+2],[-1, 0, 1]])    # sobel的x方向算子
 sobel_y = np.array([[1, 2, 1],[0,0,0],[-1, -2, -1]])     # sobel的x方向算子
 sobel_x=cv2.flip(sobel_x,-1)          # cv2.filter2D()计算的是相关，真正的卷积需要翻转，在进行相关计算。
 sobel_x=cv2.flip(sobel_y,-1)
 # cv2.flip()第二个参数：等于0：沿着x轴反转。大于0：沿着y轴反转。小于零：沿着x轴，y轴同时反转

 # 卷积 opencv是用滤波器函数实现的
 img_x=cv2.filter2D(img,-1, sobel_x)
 img_y=cv2.filter2D(img,-1, sobel_y)
 # 画图 plt不支持中文，但是可以通过以下方法设置修复
 plt.rcParams['font.sans-serif']=['SimHei']
 plt.rcParams['axes.unicode_minus'] = False

 plt.subplot(221), plt.imshow(img_x, 'gray'),plt.title('sobel_x')
 plt.subplot(222), plt.imshow(img_y, 'gray'),plt.title('sobel_y')
 plt.subplot(223), plt.imshow(img_y+img_x, 'gray'),plt.title('sobel')
 plt.subplot(224), plt.imshow(img, 'gray'),plt.title('原图')
 plt.show()

　　运行效果：

　　　　需要注意一点：在图像处理领域，卷积运算的定义是先将核关于x轴和y轴反转，然在做相关运算。然而工程实践中往往跳过反转，用相关运算代替卷积（比如opencv）。如果你需要严格的卷积运算，应该注意原函数的具体实现方式。sobel算子天生关于中心对称，所以反转与否并不影响结果（我在代码里用cv2.flip（）进行了反转操作）。

　　　　在之后的实现中，我发现用opencv自带的滤波函数算出来的梯度是归一化到（0-255）的，引入其他的库也很麻烦，因此自己写了个简单的二位卷积函数来实现梯度计算。所以上面的图适合看效果，并不适合在程序中使用，卷积函数的代码如下：

 def conv2d(src,kernel):  # 输入必须为方形卷积核
     # 本函数仍然是相关运算，没有反转。如果非要严格的卷积运算，把下面一行代码的注释取消。
     #kernel=cv2.flip(kernel,-1)
     [rows,cols] = kernel.shape
     border=rows//2                                  # 向下取整 获得卷积核边长
     [rows,cols]=src.shape
     dst = np.zeros(src.shape)                       # 采用零填充再卷积，卷积结果不会变小。
     # print("图像长：",rows,"宽：",cols,"核边界",border)
     # print(border,rows-border,border,cols-border)
     temp=[]
     for i in range(border,rows-border):
         for j in range(border,cols-border):
             temp=src[i-border:i+border+1,j-border:j+border+1]  # 从图像获取与核匹配的图像
             # 切片语法：索引位置包括开头但不包括结尾 [start: end: step]
             dst[i][j]=(kernel*temp).sum()  # 计算卷积
     return dst

　　　　小技巧：用plt显示二维矩阵，鼠标移到某个像素就会显示坐标（x，y）和灰度值，浮点数也可以显示。这可以很方便的看某个数据（像素点）是否有问题。

　　　　梯度和幅值的计算效果如下：

　

　　　　　　能看出来sobel算子计算的边缘很粗很亮，比较明显，但是不够精确，我们的目标是精确到一个像素宽，至于梯度相位就很难看出什么特征，并且梯度相位实际上是为了下一步打基础的。下面附上代码：

 img_x=conv2d(img,sobel_x)  # 使用我自己的写的卷积计算梯度
 img_y=conv2d(img,sobel_y)
 G=np.sqrt(img_x*img_x+img_y*img_y)  # 梯度幅值
 theta=np.arctan(img_y,(img_x+0.0000000000001))*180/np.pi  # 化为角度，分母+极小值是为了避免除以0
 # plt.imshow(theta, 'gray'),plt.title('梯度相位')
 plt.imshow(G, 'gray'),plt.title('梯度幅值')
 plt.show()

　　step3:非极大值抑制

　　　　　　sobel算子检测出来的边缘太粗了，我们需要抑制那些梯度不够大的像素点，只保留最大的梯度，从而达到瘦边的目的。这些梯度不够大的像素点很可能是某一条边缘的过渡点。按照高数上二位函数的极大值的定义，即对点（x0，y0）的某个邻域内所有（x，y）都有f（x，y）≤(f（x0，y0），则称f在（x0，y0）具有一个极大值，极大值为f（x0，y0）。简单方案是判断一个像素点的8邻域与中心像素谁更大，但这很容易筛选出噪声，因此我们需要用梯度和梯度方向来辅助确定。

　　　　　　如下图所示，中心像素C的梯度方向是蓝色直线，那么只需比较中心点C与dTmp1和dTmp2的大小即可。由于这两个点的像素不知道，假设像素变化是连续的，就可以用g1、g2和g3、g4进行线性插值估计。设g1的幅值M(g1)，g2的幅值M(g2),则M(dtmp1)=w*M(g2)+(1-w)*M(g1)  ，其w=distance(dtmp1,g2)/distance(g1,g2)  。也就是利用g1和g2到dTmp1的距离作为权重，来估计dTmp1的值。w在程序中可以表示为tan（θ）来表示，具体又分为四种情况（下面右图）讨论。

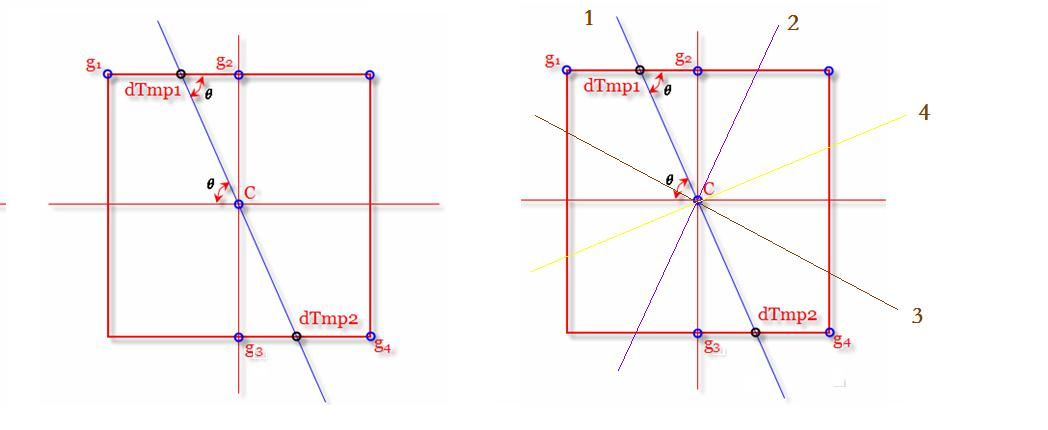
　　　　　　如下图，经过非极大值抑制可以很明显的看出去除了很多点，边缘也变得很细。在程序实现中，要注意opencv的默认坐标系是从左到右为x轴，从上到下是y轴，原点位于左上方，计算g1、g2、g3、g4的位置的时候，一定要小心（坑了我很久）。经过非极大值抑制可以看出来图片的边缘明显变细，很多看起来黑色的部分其实有值的，只是因为值太小了看不清楚，而这些黑色的部分可能是噪声或者其他原因造成的局部极大值，下一步我们就要用双阈值来限定出强边缘和弱边缘，尽可能的减少噪声的检出。代码附上：

　　　　

 # step3:非极大值抑制
 anchor=np.where(G!=0)  # 获取非零梯度的位置
 Mask=np.zeros(img.shape)

 for i in range(len(anchor[0])):
     x=anchor[0][i]
     y=anchor[1][i]
     center_point=G[x,y]
     current_theta=theta[x,y]
     dTmp1=0
     dTmp2=0
     W=0
     if current_theta>=0 and current_theta<45:
         #        g1         第一种情况
         # g4  C  g2
         # g3
         g1 = G[x + 1, y - 1]
         g2 = G[x + 1, y]
         g3 = G[x - 1, y + 1]
         g4 = G[x - 1, y]
         W=abs(np.tan(current_theta*np.pi/180))  # tan0-45范围为0-1
         dTmp1= W*g1+(1-W)*g2
         dTmp2= W*g3+(1-W)*g4

     elif current_theta>=45 and current_theta<90:
         #     g2 g1         第二种情况
         #     C
         # g3  g4

         g1 = G[x + 1, y - 1]
         g2 = G[x, y - 1]
         g3 = G[x - 1, y + 1]
         g4 = G[x, y + 1]
         W = abs(np.tan((current_theta-90) * np.pi / 180))
         dTmp1= W*g1+(1-W)*g2
         dTmp2= W*g3+(1-W)*g4

     elif current_theta>=-90 and current_theta<-45:
         # g1  g2            第三种情况
         #     C
         #     g4 g3
         g1 = G[x - 1, y - 1]
         g2 = G[x, y - 1]
         g3 = G[x + 1, y + 1]
         g4 = G[x, y + 1]
         W = abs(np.tan((current_theta-90) * np.pi / 180))
         dTmp1= W*g1+(1-W)*g2
         dTmp2= W*g3+(1-W)*g4

     elif current_theta>=-45 and current_theta<0:
         # g3                第四种情况
         # g4  C  g2
         #        g1
         g1 = G[x + 1, y + 1]
         g2 = G[x + 1, y]
         g3 = G[x - 1, y - 1]
         g4 = G[x - 1, y]
         W = abs(np.tan(current_theta * np.pi / 180))
         dTmp1= W*g1+(1-W)*g2
         dTmp2= W*g3+(1-W)*g4

     if dTmp1<center_point and dTmp2<center_point:   # 记录极大值结果
             Mask[x,y]=center_point
 #Mask=(Mask-Mask.min())/(Mask.max()-Mask.min())*256 #归一化
 plt.imshow(Mask,'gray'),plt.title('Mask')
 plt.show()

　　step4：用双阈值算法检测和连接边缘

　　　　　　双阈值法非常简单，我们假设两类边缘：经过非极大值抑制之后的边缘点中，梯度值超过T1的称为强边缘，梯度值小于T1大于T2的称为弱边缘，梯度小于T2的不是边缘。可以肯定的是，强边缘必然是边缘点，因此必须将T1设置的足够高，以要求像素点的梯度值足够大（变化足够剧烈），而弱边缘可能是边缘，也可能是噪声，如何判断呢？当弱边缘的周围8邻域有强边缘点存在时，就将该弱边缘点变成强边缘点，以此来实现对强边缘的补充。实际中人们发现T1:T2=2:1的比例效果比较好，其中T1可以人为指定，也可以设计算法来自适应的指定，比如定义梯度直方图的前30%的分界线为T1，我实现的是人为指定阈值。检查8邻域的方法叫边缘滞后跟踪，连接边缘的办法还有区域生长法等等。强边缘、弱边缘、综合效果、和opencv的canny函数对比如下：

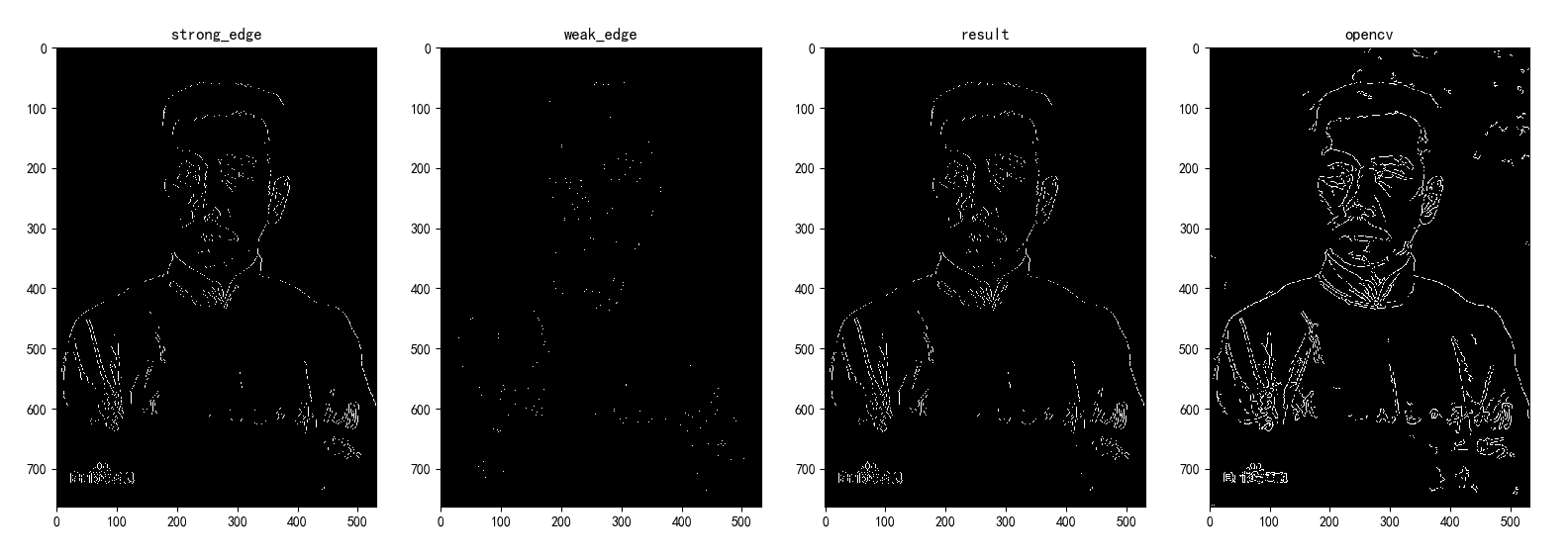
三、总结

　　　　实现结果还是很打击的，我检测到的边缘过于断续，没有opencv实现的效果好。查了一下opencv的源码，这里猜测两个可能的原因：源码里梯度的方向被近似到四个角度之一 （0，45，90，135），但我用线性插值的的结果是梯度方向更精确，而过于精确-->过于严格-->容易受到噪声干扰，所以在非极大值抑制这之后，我比opencv少了更多的点，最终导致了边缘不够连续；第二个原因可能是边缘连接算法效果不够好，把图象放大来看，我产生的边缘倾向于对角线上连接，而opencv的边缘倾向于折线连接，因此opencv的边缘更完整连续，而我的边缘更细，更容易断续。

　　　　限于时间，暂时研究到这里，希望各位多多指正！感谢所有我参考过的博客和文档！

 import cv2
 import numpy as np
 import matplotlib.pyplot as plt

 # 画图 plt不支持中文，但是可以通过以下方法设置修复
 plt.rcParams['font.sans-serif']=['SimHei']
 plt.rcParams['axes.unicode_minus'] = False

 def conv2d(src,kernel):  # 输入必须为方形卷积核
     # 本函数仍然是相关运算，没有反转。如果非要严格的卷积运算，把下面一行代码的注释取消。
     #kernel=cv2.flip(kernel,-1)
     [rows,cols] = kernel.shape
     border=rows//2                                  # 向下取整 获得卷积核边长
     [rows,cols]=src.shape
     dst = np.zeros(src.shape)                       # 采用零填充再卷积，卷积结果不会变小。
     # print("图像长：",rows,"宽：",cols,"核边界",border)
     # print(border,rows-border,border,cols-border)
     temp=[]
     for i in range(border,rows-border):
         for j in range(border,cols-border):
             temp=src[i-border:i+border+1,j-border:j+border+1]  # 从图像获取与核匹配的图像
             # 切片语法：索引位置包括开头但不包括结尾 [start: end: step]
             dst[i][j]=(kernel*temp).sum()  # 计算卷积
     return dst

 # step0:读入图片
 img=cv2.imread("images/luxun.png",cv2.IMREAD_GRAYSCALE)  # 读入图片

 # step1:高斯滤波
 img=cv2.GaussianBlur(img,(5,5),0)

 # step2:计算梯度强度和方向
 sobel_x = np.array([[-1, 0, 1],[-2,0,+2],[-1, 0, 1]])   # sobel的x方向算子
 sobel_y = np.array([[1, 2, 1],[0,0,0],[-1, -2, -1]])    # sobel的y方向算子

 # img_x=cv2.filter2D(img,-1, sobel_x)  # 这个滤波器会将卷积结果归一化到0-255，无法计算梯度方向。
 # img_y=cv2.filter2D(img,-1, sobel_y)  # 而真正的图像卷积可能会出现负数，因此只能自己写个卷积。
 img_x=conv2d(img,sobel_x)  # 使用我自己的写的卷积计算梯度
 img_y=conv2d(img,sobel_y)
 G=np.sqrt(img_x*img_x+img_y*img_y)  # 梯度幅值
 theta=np.arctan(img_y,(img_x+0.0000000000001))*180/np.pi  # 化为角度，分母+极小值是为了避免除以0

 # plt.imshow(theta, 'gray'),plt.title('梯度相位')
 # plt.imshow(G, 'gray'),plt.title('梯度幅值')
 # plt.show()
 # exit()

 # step3:非极大值抑制
 anchor=np.where(G!=0)  # 获取非零梯度的位置
 Mask=np.zeros(img.shape)
 for i in range(len(anchor[0])):
     x=anchor[0][i]  # 取出第i个非零梯度的x坐标
     y=anchor[1][i]
     center_point=G[x,y]
     current_theta=theta[x,y]
     dTmp1=0
     dTmp2=0
     W=0
     if current_theta>=0 and current_theta<45:
         #        g1         第一种情况
         # g4  C  g2
         # g3
         g1 = G[x + 1, y - 1]
         g2 = G[x + 1, y]
         g3 = G[x - 1, y + 1]
         g4 = G[x - 1, y]
         W=abs(np.tan(current_theta*np.pi/180))  # tan0-45范围为0-1
         dTmp1= W*g1+(1-W)*g2
         dTmp2= W*g3+(1-W)*g4

     elif current_theta>=45 and current_theta<90:
         #     g2 g1         第二种情况
         #     C
         # g3  g4
         g1 = G[x + 1, y - 1]
         g2 = G[x, y - 1]
         g3 = G[x - 1, y + 1]
         g4 = G[x, y + 1]
         W = abs(np.tan((current_theta-90) * np.pi / 180))
         dTmp1= W*g1+(1-W)*g2
         dTmp2= W*g3+(1-W)*g4
     elif current_theta>=-90 and current_theta<-45:
         # g1  g2            第三种情况
         #     C
         #     g4 g3
         g1 = G[x - 1, y - 1]
         g2 = G[x, y - 1]
         g3 = G[x + 1, y + 1]
         g4 = G[x, y + 1]
         W = abs(np.tan((current_theta-90) * np.pi / 180))
         dTmp1= W*g1+(1-W)*g2
         dTmp2= W*g3+(1-W)*g4
     elif current_theta>=-45 and current_theta<0:
         # g3                第四种情况
         # g4  C  g2
         #        g1
         g1 = G[x + 1, y + 1]
         g2 = G[x + 1, y]
         g3 = G[x - 1, y - 1]
         g4 = G[x - 1, y]
         W = abs(np.tan(current_theta * np.pi / 180))
         dTmp1= W*g1+(1-W)*g2
         dTmp2= W*g3+(1-W)*g4

     if dTmp1<center_point and dTmp2<center_point:   # 记录极大值结果
             Mask[x,y]=center_point
 # plt.imshow(Mask,'gray'),plt.title('Mask')
 # plt.show()
 # exit()

 # step4:双阈值选取
 high_threshold=100
 low_threshold=high_threshold/2
 strong_edge=np.zeros(G.shape)   # 强边缘
 weak_edge=np.zeros(G.shape)     # 弱边缘

 xNum = [1, 1, 0, -1, -1, -1, 0, 1]  # 8邻域偏移坐标
 yNum = [0, 1, 1, 1, 0, -1, -1, -1]
 [rows, cols] = G.shape
 for i in range(rows):
     for j in range(cols):
         current_point=Mask[i,j]
         if current_point>0:
             if current_point>high_threshold:   # 强边缘提取
                 strong_edge[i,j]=255
             elif current_point<high_threshold and current_point>low_threshold:  # 弱边缘提取
                 # step6:顺便进行边缘连接
                 change = True
                 while change:
                     change = False
                     for k in range(8):
                         xx=i+xNum[k]
                         yy=j+yNum[k]
                         if Mask[xx,yy]>high_threshold:
                             weak_edge[i, j] = 255
                             break  # 跳出八邻域循环
 output=strong_edge+weak_edge    # 强弱边缘综合效果

 img_edge = cv2.Canny(img, 50, 100)  # opencv实现效果

 # 显示效果
 plt.subplot(141), plt.imshow(strong_edge, 'gray'),plt.title('strong_edge')
 plt.subplot(142), plt.imshow(weak_edge, 'gray'),plt.title('weak_edge')
 plt.subplot(143), plt.imshow(output, 'gray'),plt.title('result')
 plt.subplot(144), plt.imshow(img_edge, 'gray'),plt.title('opencv')
 plt.show()

完整代码

　　参考文献：

　　　　 https://www.cnblogs.com/love6tao/p/5152020.html

　　　　 https://www.cnblogs.com/techyan1990/p/7291771.html

　　　   https://www.cnblogs.com/centor/p/5937788.html

　　　   https://blog.csdn.net/piaoxuezhong/article/details/62217443