前/后向自动微分的简单推导与rust简单实现

自动微分不同于数值微分与符号微分, 能够在保证速度的情况下实现高精度的求某个可微函数的定点微分值. 下面将简要介绍其原理, 并给出 rust 的两种微分方式的基本实现.

微分方法简介

数值微分

利用微分的定义式

\[f'(x) = \lim_{h\to 0} \frac{f(x+h)-f(x)}{h}
\]

因此可以用割线斜率公式近似微分, 当 \(h\) 足够小时割线将与切线重合.

\[f'(x) \approx \frac{f(x+h) - f(x)}{h}
\]

数值微分存在两个缺点:

• \(h\) 的取值, 要保证 \(h\to 0\), 才能保证割线足够接近切线, 但当 \(h\) 过小时容易因浮点误差导致数值不稳定, 尤其当导数变化剧烈时, 可能需要反复调整 \(h\) 来找到合适的精度.
• 精度不足, 误差项与 \(h\) 有效数字的平方成正比, 也就是说即使最理想情况下, 在f64范围内, \(h\) 取 1e-16 (接近f4的精度极限), 误差项也只有 1e-8 的精度.

通过多个点参与计算能提升精度, 下面提供 Wikipedia 中一个五点公式:

\[f'(x)\approx \frac{-f(x+2h) + 8f(x+h) -8f(x-h) + f(x-2h)}{12h}
\]

优势在于若无法得到函数表达式, 但可以求特定点值时可以直接使用, 而符号微分和自动微分在无表达式的情况下, 需要通过插值等方式拿到一个表达式.

符号微分

首先定义好常用函数的微分规则, 在已经取得表达式的条件下, 解析表达式得到一个计算树, 然后自下而上或自上而下对树的每个计算节点运用微分规则, 最后就能得到微分后的表达式, 下面用 \(f(x) = \sin(x + x^2)/\sqrt x\) 为例给出计算图例:



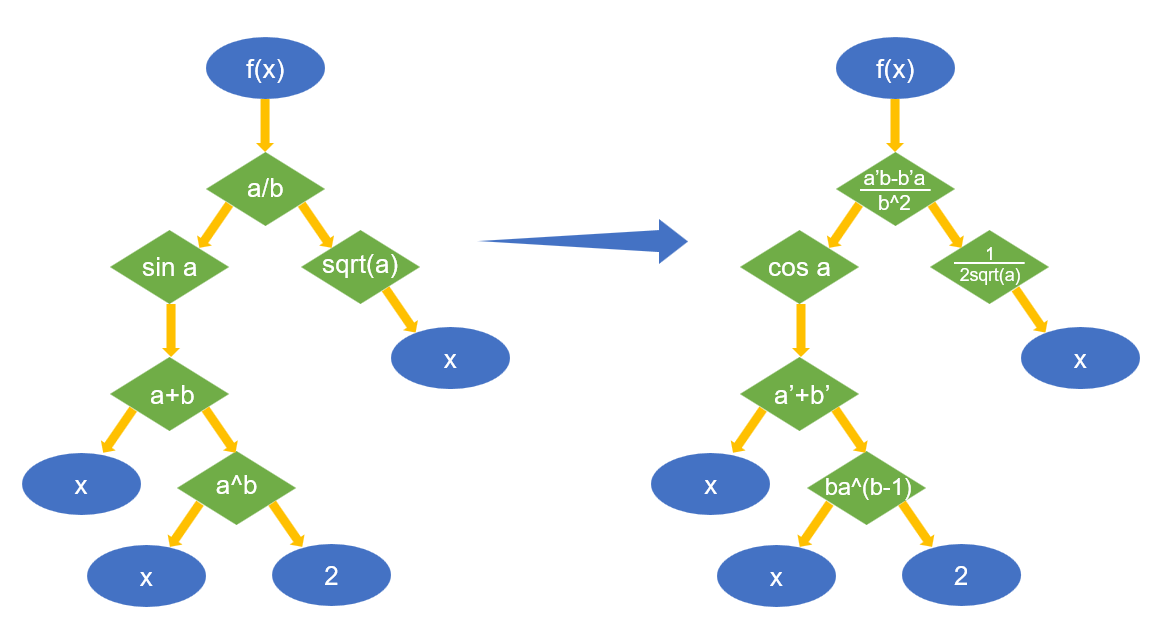
可以看到只要对节点运用微分规则, 就能求出最终的微分式为: \(f'(x)=(\sqrt x\cos(x+x^2)(1+2x)-\sin(x+x^2)/2\sqrt x)/x\)

中间有一些细节需要处理, 比如pow函数要处理 \(x^a, a^x, x^x\) 这三种不同导数的形式, 其次对于多元函数偏导需要标记把哪个变量当变量, 哪些变量当常数, 由于本位重点在于自动微分, 故此处不再深入.

符号微分存在缺点:

• 需要显式的表达式(有些改进能处理隐式表达式), 对于无表达式的函数需要通过插值等方法获得近似的表达式.
• 需要额外存储一棵表达式树和一棵微分表达式树.
• 存在表达式膨胀的隐患, 比如 \(d(x+1)(x+2)(x+3)/dx=(x+1)(x+2)+(x+1)(x+3)+(x+2)(x+3)\), 项数从1变成3, 若包含指数函数, 三角函数等的复杂多项函数可能会得到一个非常庞大的微分表达式树, 若求高阶导数会更膨胀.
• 实现难度大, 运行效率相对慢
  
  优势在于:
• 能精确得到微分后的表达式, 这样就可以进一步求高阶导数(插值得到的表达式可能会不稳定).
• 精度理论上和手动计算编写的函数是一样的

自动微分

自动微分在细节上类似于符号微分, 但利用了微分的定义式将中间结果直接求值, 从而避免了表达式膨胀的问题, 效率提升的同时保证了精度. 自动微分最常见的方案基于对偶数, 同时根据求值的顺序分为前向自动微分和后向自动微分, 下面将逐一介绍.

对偶数

回到微分的定义式

\[f'(x) = \lim_{h\to 0} \frac{f(x+h)-f(x)}{h}
\]

我们定义 \(\varepsilon\), 其定义为一个无限趋于0的过程 (注意是过程而不是数, 实数域内不存在无穷小量). 不严谨的说, 可以将 \(\varepsilon\) 定义成 1 个算子, 其作用的量将取如下极限:

\[\varepsilon a=\lim_{a\to0}a
\]

这样一来, \(\varepsilon a\) 就和 \(\mathrm{d}a\) 有很相似的性质.

我们定义一种新的数, 仿照复数给出一个简写:

\[A+\varepsilon a = (A, a)
\]

本文将 \(A\) 称为数部, \(a\) 称为微分部. 这个数对 \((A,a)\) 就是对偶数.

基于对偶数的定义, 很容易可以得到其四则运算性质:

\[\begin{align*}
(A,a)\pm (B,b) &=(A\pm B, a\pm b) \\
k \times (A,a) &= (A,a) \times k = (kA, ka) \\
(A,a) \times (B,b) &= (AB, aB+Ab) \cancel{+ \varepsilon^2ab} \\
\frac{(A, a)}{(B,b)} &= (\frac{A}{B},\frac{aB-Ab}{B^2})
\end{align*}
\]

在乘除运算中会出现二阶无穷小, 其在一阶微分中会被消除, 所以去掉该项.

对于所有一元函数有:

\[\begin{align*}
f((A,a))&=f(A+\varepsilon a)\\
&=f(A+\varepsilon a)-f(A)+f(A)\\
&=\frac{f(A+\varepsilon a)-f(A)}{\varepsilon a}\varepsilon a+f(A)\\
&=\lim_{a\to0}\frac{f(A+a)-f(A)}{a}\varepsilon a+f(A)\\
&=f'(A)\varepsilon a+f(A)\\
&=(f(A),f'(A)a)
\end{align*}
\]

这样就能快速得到一系列公式:

\[\begin{align*}
\sin(A,a)&=(\sin A,a\cos A)\\
\cos(A,a)&=(\cos A,-a\sin A)\\
\exp(A,a)&=(\exp A, a\exp A)\\
\ln(A,a)&=(1/A,a/A)\\
(A,a)^n&=(A^n, nA^{n-1}a)\\
n^{(A,a)}&=(n^A, n^A \ln A a)\\
\dots
\end{align*}
\]

对于所有二元函数则有(推导和一元函数基本一致, 此处略):

\[f((A,a),(B,b))=(f(A,B),\frac{\partial f}{\partial A}a+\frac{\partial f}{\partial B}b)
\]

可得一系列公式:

\[\begin{align*}
(A,a)^{(B,b)}&=(A^B,BA^{B-1}a+A^B\ln Ab)\\
\log_{(B,b)}{(A,a)}&=(\log_B A,\frac{a}{A \ln B}-\frac{b\log_B A}{B \ln B})\\
\dots
\end{align*}
\]

值得注意的是, 令 \((A,a)\) 中微分部 \(a=1\), 其他变量的微分部全为 \(0\), 此时运算结果中的微分部将会是 \(\partial f/\partial A\)!

下面以 \(f(x,y) = \sin(x + y^2)/\sqrt x\) 为例, 求 \(x=2, y=1\) 处对 \(x\) 的偏导数:

\[\begin{align*}
f((2, 1),(1,0)) &= \sin((2,1) + (1,0)^2)/\sqrt {(2,1)}\\
&=\sin((2,1) + (1,0))/(\sqrt{2},1/2\sqrt{2})\\
&=\sin((3,1))/(\sqrt{2},1/2\sqrt{2})\\
&=(\sin(3), \cos(3))/(\sqrt{2},1/2\sqrt{2})\\
&=(\frac{\sin(3)}{\sqrt{2}}, \frac{\cos(3)}{\sqrt{2}}-\frac{\sin(3)}{2}\frac{1}{2\sqrt{2}})\\
&=(0.0997869, -0.724977)
\end{align*}
\]

基于以上原理, 很容易就能得到前向自动微分算法.

前向自动微分

通过对对偶数的分析, 我们可以用一个结构体包裹数部和微分部, 并重载或实现其常用的数学运算, 利用这些运算的组合, 自下而上得到整个函数的微分, 即可实现前向自动微分. 如 \(f(h(g(x,y)))\) 有

\[\frac{\partial f}{\partial x}=\frac{\partial g}{\partial x}\frac{\partial h}{\partial g}\frac{\partial f}{\partial h}
\]

对偶数的结构

定义微分变量结构体:

#[derive(Clone, Copy)]
pub struct Variable {
    value: f64,
    grad: f64,
}

impl Variable {
    pub fn new(value: f64) -> Self {
        Self { value, grad: 0.0 }
    }
    pub fn new_diff(value: f64) -> Self {
        Self { value, grad: 1.0 }
    }
    pub fn grad(self) -> f64 {
        self.grad
    }
    pub fn value(self) -> f64 {
        self.value
    }
    pub fn value_grad(self) -> (f64, f64) {
        (self.value, self.grad)
    }
}

重载运算

重载四则运算, 仅展示加法和除法:

use std::ops::{Add, Div};
impl Add for Variable {
    type Output = Self;
    fn add(self, rhs: Self) -> Self::Output {
        Self {
            value: self.value + rhs.value,
            grad: self.grad + rhs.grad,
        }
    }
}

impl Add<f64> for Variable {
    type Output = Self;
    fn add(self, rhs: f64) -> Self::Output {
        Self {
            value: self.value + rhs,
            ..self
        }
    }
}

impl Div for Variable {
    type Output = Self;
    fn div(self, rhs: Self) -> Self::Output {
        let value = self.value / rhs.value;
        Self {
            value,
            grad: value + (self.grad - value * rhs.grad) / rhs.value,
        }
    }
}

impl Div<f64> for Variable {
    type Output = Self;
    fn div(self, rhs: f64) -> Self::Output {
        Self {
            value: self.value / rhs,
            grad: self.grad / rhs,
        }
    }
}

实现数学函数

实现其他数学函数, 仅展示几个典型的

impl Variable {
    pub fn sin(self) -> Self {
        Self {
            value: self.value.sin(),
            grad: self.value.cos() * self.grad,
        }
    }

    pub fn log(self, base: f64) -> Self {
        Self {
            value: self.value.log(base),
            grad: self.grad / (self.value * base.ln()),
        }
    }

    pub fn logx(self, base: Self) -> Self {
        let ln_b_recip = base.value.ln().recip();
        let value = self.value.log(base.value);
        Self {
            value,
            grad: ln_b_recip * self.value * self.grad + value * ln_b_recip * base.grad / base.value,
        }
    }
}

使用方法

实现以上一系列函数后, 即可如下使用前向自动微分:

fn forward_diff_works() {
    use crate::forward::Variable;

    // 支持闭包和函数, 要求输入和输出都是Variable类型: f(x)=sin(exp(x))
    let f = |x: Variable| -> Variable { x.exp().sin() };
    // 求 x 的微分, 定义变量 x = (3, 1)
    let x = Variable::new_diff(3.0);
    // 计算 df/dx (x = 3.0) 接近 6.6
    let grad = f(x).grad();
    assert!((grad - 6.6).abs() < 1e-5);

    // 定义二维函数, f(x) = sqrt(x^2 + y^2)
    let f = |x: Variable, y: Variable| -> Variable { (x.powi(2) + y.powi(2)).sqrt() };
    // 求 x 的偏导, 定义 x = (3, 1), y = (4, 0)
    let x = Variable::new(3.0);
    let y = Variable::new_diff(4.0);

    // 计算 f(x,y) 和 ∂f/∂y (x = 3.0, y = 4.0)
    let (value, grad) = f(x, y).value_grad();
    assert!((value - 5.0).abs() < 1e-12);
    }

前向自动微分的原理相对简单, 通过对每个计算过程的微分一步步组合成最终的微分, 但缺点是每次只能求一个变量的微分, 如果有多个变量, 需要多次计算, 所以前向自动微分适合参数少的函数 (如果扩展到向量, 则适合输出多于输入的函数).

后向自动微分

后向自动微分针对前向自动微分的缺点, 其可以通过一次微分得到函数对所有参数的偏导数, 其不是自下而上一步步组合每个微分, 而是自上而下从总式开始一步步展开, 最后得到导数. 如 \(f(h(g(x,y)))\) 有:

\[\frac{\partial f}{\partial x}=\frac{\partial f}{\partial h}\frac{\partial h}{\partial g}\frac{\partial g}{\partial x}
\]

可以看到计算顺序是前向微分颠倒过来的. 但在编程中, 定义函数是通过变量自下而上组合得到的, 所以后向自动微分不能像前向自动微分一样在定义函数的同时直接得到, 而是需要保存整个计算结构, 类似之前符号微分的表达式树 自上而下解析数的同时对节点进行微分处理.

保存后向自动微分通常采用计算图, 以 \(f(x,y) = \sin(x + y^2)/\sqrt x\) 为例, 下面是其计算图的图例:

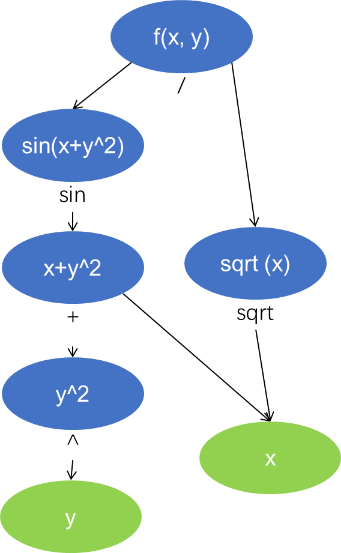
可以看到相比表达式树, 其重用了变量, 可减少后续计算量. 同时该树的求导为自上而下, 故构成一个有向无环图(DAG).

计算图的储存形式

通过对偶数原理, 可以知道每个 Node 储存一个对偶数, 此外为了记录图信息, 还要额外记录该节点类型

struct Node {
    node_type: NodeType,
    value: f64,
    grad: f64,
}

Graph 中存放Node数组, 这样就可以通过索引得到图中的节点:

pub struct Graph<const N: usize> {
    nodes: Vec<Node>,
}

NodeType 为该节点计算的表达式类型, 同时记录参与运算的节点下标等信息, 比如某个节点记录两节点加法, 则为 AddX 类型, 其包含的两个 usize 为其左右运算节点在图中的下标; 如果某个节点记录节点加常数, 则为 Add 类型, 其包含的 usize 为节点的下标, f64 为加数, 下面给出几个常见函数的示例:

enum NodeType {
    Variable,
    AddX(usize, usize),
    Add(usize, f64)
    Sin(usize),
    Powf(usize, f64),
    PowX(usize, usize),
}

最后是Variable, 其本质上是图中的一个节点, 同时在变量运算时需要找到他们所在的图, 所以还包含一个所在图的指针:

#[derive(Clone, Copy)]
pub struct Variable<const N: usize> {
    graph: NonNull<Graph<N>>,
    id: usize,
}

以上代码中有两处小细节

1. Variable中的指针用的是不安全的 NonNull 而不是 Rc<RefCell<Graph>>, 这是为了实现 Copy trait方便使用, 否则最后定义函数时需要类似以下语法:

let f = &x + &y;
let f = x.clone() + y.clone();

使用 NonNull 并实现 Copy trait 可以写为:

let f = x + y;

1. Graph定义时使用了 const 泛型, 导致 Variable 定义也要有 const 泛型, 这是防止两个不同图中的节点相互计算

let mut graph1:Graph<0> = Graph::new();
let x = graph1.new_variable(3.0);
let mut graph2:Graph<1> = Graph::new();
let y = graph2.new_variable(4.0);
let f = x + y;

通过const 泛型标记图的类型, x 和 y 将会有不同的变量类型, 在编译器就可以避免两者间的运算.

变量与图的构建

通过如下过程创建变量与建立计算图

use std::{
    ops::Add,
    ptr::NonNull,
};

impl<const N: usize> Graph<N> {
    pub fn new() -> Self {
        Self { nodes: Vec::new() }
    }

    pub fn new_variable(&mut self, value: f64) -> Variable<N> {
        let id = self.nodes.len();
        let node = Node {
            node_type: NodeType::Variable,
            value,
            grad: 0.0,
        };
        self.nodes.push(node);
        Variable {
            graph: NonNull::from(self),
            id,
        }
    }
}

impl<const N: usize> Add for Variable<N> {
    type Output = Self;
    fn add(self, rhs: Self) -> Self::Output {
        let mut lhs = self;
        let graph = unsafe { lhs.graph.as_mut() };
        let id = graph.nodes.len();
        let node = Node {
            node_type: NodeType::AddX(self.id, rhs.id),
            value: graph.nodes[self.id].value + graph.nodes[rhs.id].value,
            grad: 0.0,
        };
        graph.nodes.push(node);
        Variable {
            graph: NonNull::from(graph),
            id,
        }
    }
}
impl<const N: usize> Add<f64> for Variable<N> {
    type Output = Self;
    fn add(self, rhs: f64) -> Self::Output {
        let mut lhs = self;
        let graph = unsafe { lhs.graph.as_mut() };

        let id = graph.nodes.len();
        let node = Node {
            node_type: NodeType::Add(self.id, rhs),
            value: graph.nodes[self.id].value + rhs,
            grad: 0.0,
        };
        graph.nodes.push(node);
        Variable {
            graph: NonNull::from(graph),
            id,
        }
    }
}

通过new_variable创建一个与图绑定的变量并赋初值.

为变量实现各种数学运算, 这里仅以Add为例, 在运算时计算数部的运算, 微分部暂时不运算, 该部分放到计算图构建结束后自上而下计算. 在计算的同时创建对应运算类型的节点, 并存放到计算图中.

后向微分过程

前面构建了计算图, 在图构建好后, 其数组中自下而上依序存放着节点, 将节点逆序遍历并应用微分法则, 即可进行后向微分求解, 由于自上而下求解, 每个变量的偏导数都将存放到它对应的微分部, 所以后向微分只要一次计算就能得到所有变量的偏导数. 通过 grad 函数和 value 函数输出对应变量的微分值和计算值.

impl<const N: usize> Graph<N> {
    pub fn grad(&self, x: Variable<N>) -> f64 {
        self.nodes[x.id].grad
    }
    pub fn value(&self, f: Variable<N>) -> f64 {
        self.nodes[f.id].value
    }

    pub fn backward(&mut self, output: Variable<N>) {
        self.nodes[output.id].grad = 1.0;
        for i in (0..self.nodes.len()).rev() {
            let grad_out = self.nodes[i].grad;
            if grad_out == 0.0 {
                continue;
            }

            match self.nodes[i].node_type {
                NodeType::Variable => {}
                NodeType::AddX(l_id, r_id) => {
                    self.nodes[l_id].grad += grad_out;
                    self.nodes[r_id].grad += grad_out;
                }
                NodeType::Add(l_id, _rhs) => {
                    self.nodes[l_id].grad += grad_out;
                }
            }
        }
    }
}

由于后向自动微分一次求解能得到所有偏导的特点, 所以适合参数多而输出少的函数.

使用方法

基于以上代码, 后向自动微分使用方法如下:

fn main() {
    // 创建计算图
    let mut graph: Graph<0> = Graph::new();
    // 定义变量
    let x = graph.new_variable(3.0);
    // 构建计算图
    let f = x.exp().sin();
    // 后向微分过程
    graph.backward(f);
    // 得到 df/dx (x = 3.0)
    let grad = graph.grad(x);
    assert!((grad - 6.6).abs() < 1e-5);

    let mut graph: Graph<1> = Graph::new();
    let x = graph.new_variable(3.0);
    let y = graph.new_variable(4.0);
    let f = (x.powi(2) + y.powi(2)).sqrt();
    graph.backward(f);
    // 同时得到两个偏导
    let f_x = graph.grad(x);
    let f_y = graph.grad(y);
    let value = graph.value(f);
    assert!((value - 5.0).abs() < 1e-12);
    assert!((f_x - 0.6).abs() < 1e-12);
    assert!((f_y - 0.8).abs() < 1e-12);
}

总结

三种自动微分都有其适用范围, 其中自动微分的前向微分模式和后向微分模式优缺点互补:

• 前向自动微分编写简单, 空间占用小, 单次运行速度更快, 一次只能求一个变量对所有函数的偏导数, 适合参数少而输出多的函数. 常用于日常的简单计算.
• 后向自动微分编写复杂, 空间占用大, 需要正相构建计算图+后向微分两次运行, 单次运行速度较慢, 但一次能求一个函数所有变量的偏导数, 适合参数多而输出少的函数. 常用于机器学习等超多变量的情况.
  
  这里给出一个完整实现, 供各位参考, 其中example中有利用前向自动微分+牛顿迭代法求函数零点的示例.