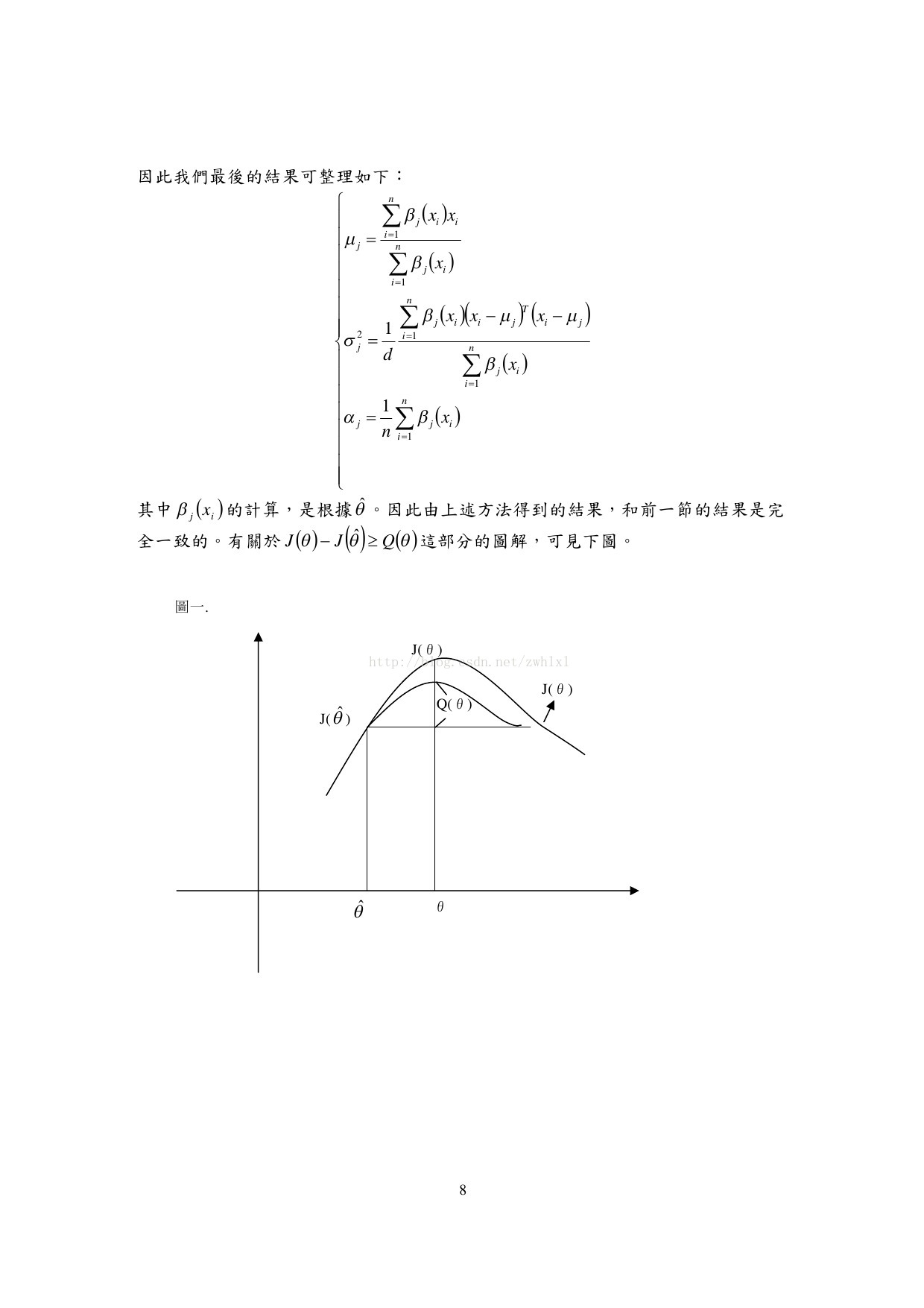
[转]GMM:高斯混合模型讲义(台湾)







[转]GMM:高斯混合模型讲义(台湾)的更多相关文章
- GMM高斯混合模型学习笔记(EM算法求解)
提出混合模型主要是为了能更好地近似一些较复杂的样本分布,通过不断添加component个数,能够随意地逼近不论什么连续的概率分布.所以我们觉得不论什么样本分布都能够用混合模型来建模.由于高斯函数具有一 ...
- K-Means(K均值)、GMM(高斯混合模型),通俗易懂,先收藏了!
1. 聚类算法都是无监督学习吗? 什么是聚类算法?聚类是一种机器学习技术,它涉及到数据点的分组.给定一组数据点,我们可以使用聚类算法将每个数据点划分为一个特定的组.理论上,同一组中的数据点应该具有相似 ...
- opencv::GMM(高斯混合模型)
GMM方法概述:基于高斯混合模型期望最大化. 高斯混合模型 (GMM) 高斯分布与概率密度分布 - PDF 初始化 初始化EM模型: Ptr<EM> em_model = EM::crea ...
- GMM高斯混合模型 学习(2)
watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvaHpxMjAwODExMjExMDc=/font/5a6L5L2T/fontsize/400/fill/I0 ...
- EM算法和高斯混合模型GMM介绍
EM算法 EM算法主要用于求概率密度函数参数的最大似然估计,将问题$\arg \max _{\theta_{1}} \sum_{i=1}^{n} \ln p\left(x_{i} | \theta_{ ...
- 高斯混合模型GMM与EM算法的Python实现
GMM与EM算法的Python实现 高斯混合模型(GMM)是一种常用的聚类模型,通常我们利用最大期望算法(EM)对高斯混合模型中的参数进行估计. 1. 高斯混合模型(Gaussian Mixture ...
- 高斯混合模型(GMM)
复习: 1.概率密度函数,密度函数,概率分布函数和累计分布函数 概率密度函数一般以大写“PDF”(Probability Density Function),也称概率分布函数,有的时候又简称概率分布函 ...
- paper 62:高斯混合模型(GMM)参数优化及实现
高斯混合模型(GMM)参数优化及实现 (< xmlnamespace prefix ="st1" ns ="urn:schemas-microsoft-com:of ...
- 贝叶斯来理解高斯混合模型GMM
最近学习基础算法<统计学习方法>,看到利用EM算法估计高斯混合模型(GMM)的时候,发现利用贝叶斯的来理解高斯混合模型的应用其实非常合适. 首先,假设对于贝叶斯比较熟悉,对高斯分布也熟悉. ...
- 高斯混合模型(GMM) - 混合高斯回归(GMR)
http://www.zhihuishi.com/source/2073.html 高斯模型就是用高斯概率密度函数(正态分布曲线)精确地量化事物,将一个事物分解为若干的基于高斯概率密度函数(正态分布曲 ...
随机推荐
- 云原生周刊:Docker 推出 Docker Build Cloud
开源项目推荐 Kube-Vip Kube-Vip 旨在为 Kubernetes 集群提供高可用性和负载均衡功能.它提供了一个可插拔的 VIP(虚拟 IP)管理器,可以为集群中的服务分配一个虚拟 IP ...
- 一个docker容器中只运行一个Service
基于单一原则,一个容器里只运行一个主进程,即一个service(进程)做成一个docker镜像.多个进程在一个容器里有很多弊端,比如一个主进程更新时,其他进程也被迫重启.容器=应用+执行应用的环境 而 ...
- IDEA久违了!FeignX插件支持方法级别的导航跳转
> 需求调研:发现身边的同事追踪业务代码的时候,如果遇见feign接口,大家都是通过全局搜url进一步找到远程服务的实现.一旦项目大起来,路径变得复杂甚至重名之后,这将会是灾难. 市面上并没有很 ...
- RTCP报文解析
RTCP包的头部结构体定义 struct RTCP_Header { unsigned short rc:5; unsigned short padding:1; unsigned short ver ...
- GPU 环境搭建指南:如何在裸机、Docker、K8s 等环境中使用 GPU
本文主要分享在不同环境,例如裸机.Docker 和 Kubernetes 等环境中如何使用 GPU. 跳转阅读原文:GPU 环境搭建指南:如何在裸机.Docker.K8s 等环境中使用 GPU 1. ...
- 基于Java+SpringBoot+Mysql实现的快递柜寄取快递系统功能实现十
一.前言介绍: 1.1 项目摘要 随着电子商务的迅猛发展和城市化进程的加快,快递业务量呈现出爆炸式增长的趋势.传统的快递寄取方式,如人工配送和定点领取,已经无法满足现代社会的快速.便捷需求.这些问题不 ...
- 题解:CF687C The Values You Can Make
CF687C The Values You Can Make 题解 题目翻译感觉不明不白的(至少我看了几遍没看懂),这里给个较为清晰的题面. 题目描述 给你 \(n\) 个硬币,第 \(i\) 个硬币 ...
- Nuxt.js 应用中的 vite:extendConfig 事件钩子详解
title: Nuxt.js 应用中的 vite:extendConfig 事件钩子详解 date: 2024/11/12 updated: 2024/11/12 author: cmdragon e ...
- 16.Kubernetes集群资源监控
Kubernetes集群资源监控 概述 监控指标 一个好的系统,主要监控以下内容 集群监控 节点资源利用率 节点数 运行Pods Pod监控 容器指标 应用程序[程序占用多少CPU.内存] 监控平台 ...
- vagrant 环境安装(前置篇)
ubuntu可以直接 apt 源查找 sudo apt search vagrant 直接就 sudo apt-get install vagrant 如果版本不是 2.2.6 可以去 https:/ ...
