题解：AT_abc385_f [ABC385F] Visible Buildings

小学二年级就会的基本一次函数知识。

抽象一下题意：

求 \(n\) 个点 \((X_i, H_i)\) 中任意两个点组成的直线的截距的最大值（不小于 \(0\)，\(X_i\) 递增）。

---

先说结论：先特判 \(n = 1\)，然后答案只可能是由编号相邻的两个点组成的一次函数的截距。

为了方便，我们记 \(B\{(a, b), (c, d)\}\) 为 \((a, b)\)、\((c, d)\) 两点组成的一次函数的截距。

若 \(B \{ (X_i, H_i), (X_{i + 1}, H_{i + 1}) \} \lt B \{ (X_{i - 1}, H_{i - 1}), (X_{i + 1}, H_{i + 1}) \}\)；

则必有 \(B \{ (X_{i - 1}, H_{i - 1}), (X_{i + 1}, H_{i + 1}) \lt B \{ (X_{i - 1}, H_{i - 1}), (X_{i}, H_{i}) \}\)。

证明：

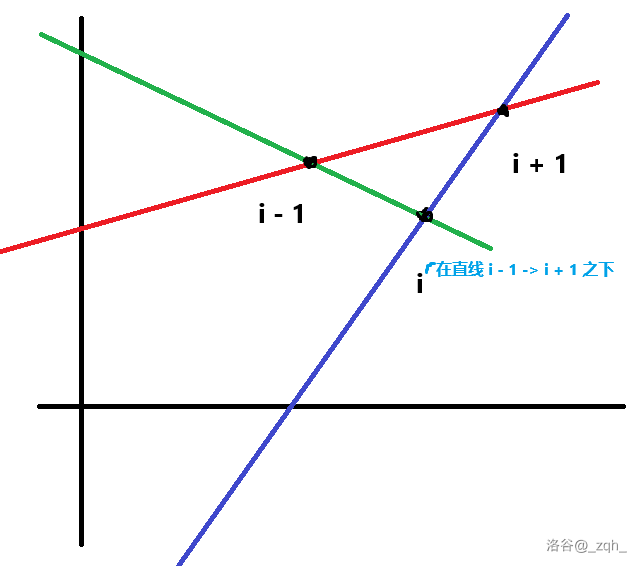
根据已知条件，\((X_i, H_i)\) 必在直线 \((X_{i - 1}, H_{i - 1}) \leftrightarrow (X_{i + 1}, H_{i + 1})\) 之下。

那么 \((X_{i + 1}, H_{i + 1})\) 就在直线 \((X_{i - 1}, H_{i - 1}) \leftrightarrow (X_{i}, H_{i})\) 之上。

（可能语言有点疏漏太抽象，看图就好理解了）

（注：上文结论可以用三角形的性质来严格证明，读者自证不难）

那么只需要枚举出任意两个编号相邻的点算一次函数的截距，并取最大值即可。

---

如果你不知道一次函数相关知识，那就别做这题学习一下罢。

给一个斜率与截距的计算公式：

\[k = \frac{y_1 - y_2}{x_1 - x_2}, b = y_1 - k \times x_1
\]

不给代码了。