洛谷 P3629 [APIO2010]巡逻 解题报告

P3629 [APIO2010]巡逻

题目描述

在一个地区中有 n 个村庄，编号为 1, 2, ..., n。有 n – 1 条道路连接着这些村 庄，每条道路刚好连接两个村庄，从任何一个村庄，都可以通过这些道路到达其 他任一个村庄。每条道路的长度均为 1 个单位。 为保证该地区的安全，巡警车每天要到所有的道路上巡逻。警察局设在编号 为 1 的村庄里，每天巡警车总是从警察局出发，最终又回到警察局。 下图表示一个有 8 个村庄的地区，其中村庄用圆表示（其中村庄 1 用黑色的 圆表示），道路是连接这些圆的线段。为了遍历所有的道路，巡警车需要走的距 离为 14 个单位，每条道路都需要经过两次。

为了减少总的巡逻距离，该地区准备在这些村庄之间建立 K 条新的道路， 每条新道路可以连接任意两个村庄。两条新道路可以在同一个村庄会合或结束 （见下面的图例（c））。 一条新道路甚至可以是一个环，即，其两端连接到同一 个村庄。 由于资金有限，K 只能是 1 或 2。同时，为了不浪费资金，每天巡警车必须 经过新建的道路正好一次。 下图给出了一些建立新道路的例子：

在(a)中，新建了一条道路，总的距离是 11。在(b)中，新建了两条道路，总 的巡逻距离是 10。在(c)中，新建了两条道路，但由于巡警车要经过每条新道路 正好一次，总的距离变为了 15。 试编写一个程序，读取村庄间道路的信息和需要新建的道路数，计算出最佳 的新建道路的方案使得总的巡逻距离最小，并输出这个最小的巡逻距离。

输入输出格式

输入格式：

第一行包含两个整数 n, K(1 ≤ K ≤ 2)。接下来 n – 1 行，每行两个整数 a, b， 表示村庄 a 与 b 之间有一条道路(1 ≤ a, b ≤ n)。

输出格式：

输出一个整数，表示新建了 K 条道路后能达到的最小巡逻距离。

说明

10%的数据中，n ≤ 1000, K = 1；

30%的数据中，K = 1；

80%的数据中，每个村庄相邻的村庄数不超过 25；

90%的数据中，每个村庄相邻的村庄数不超过 150；

100%的数据中，3 ≤ n ≤ 100,000, 1 ≤ K ≤ 2。

---

遇到这种题当然选择手玩数据啦

我们发现：对于初始的树，每条边得经过两次，当连出一个环时，环上的边全都只经过了一次。

那么k=1的30分就拿到了，求出树的直径，统计答案即可。

---

k=2时，网上大多数的做法是把直径上的边权置-1再求一遍直径，我提供一种大同小异却麻烦一点的做法（可能对我来说比较好想吧）

对链上的每个点，我们以它为根做一遍树的直径，不经过直径上的点，统计出这颗子树的直径和它的最大深度。

直径可以直接更新答案，但这样并不全，可能会有以下一种情况

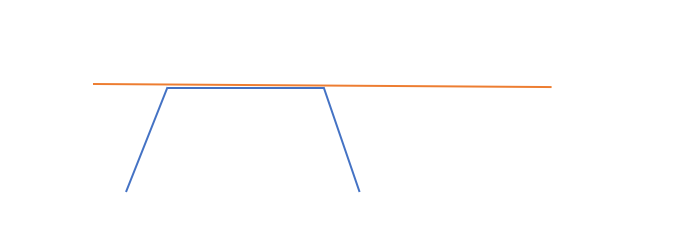
黄链为直径，而紫链为第二次连出的环。

最大深度就在这时候用一下，从左至右扫描一遍直径，用单调队列维护当前最优深度（记得减去原本在直径上的边），更新答案即可

---

Code：

#include <cstdio>
#include <cstring>
int max(int x,int y){return x>y?x:y;}
const int N=100010;
int head[N],to[N<<1],next[N<<1],F[N],cnt,dis[N],mx,mxl,l,r,n,k,q[N][2],is[N],f[N];
void add(int u,int v)
{
    to[++cnt]=v;next[cnt]=head[u];head[u]=cnt;
}
void dfs1(int now,int len,int fa)
{
    if(len>mxl)
    {
        l=now;
        mxl=len;
    }
    for(int i=head[now];i;i=next[i])
    {
        int v=to[i];
        if(!is[v]&&fa!=v)
            dfs1(v,len+1,now);
    }
}
void dfs2(int now,int len,int fa)
{
    if(mx<len)
    {
        r=now;
        mx=len;
    }
    for(int i=head[now];i;i=next[i])
    {
        int v=to[i];
        if(!is[v]&&fa!=v)
        {
            f[v]=now;
            dfs2(v,len+1,now);
        }
    }
}
void get_d(int s)
{
    mx=0,mxl=0,l=0,r=0;
    dfs1(s,0,0);
    is[s]=0;
    dfs2(l,0,0);
    is[s]=1;
}
int main()
{
    scanf("%d%d",&n,&k);
    int u,v;
    for(int i=1;i<n;i++)
    {
        scanf("%d%d",&u,&v);
        add(u,v),add(v,u);
    }
    get_d(1);
    is[1]=0;
    int L=l,R=r,D=mx,ans=0;
    if(k>1)
    {
        int now=R;
        while(now)
        {
            is[now]=1;
            F[now]=f[now];
            now=f[now];
        }
        for(int i=1;i<=n;i++)
            if(is[i])
            {
                get_d(i);
                dis[i]=mxl;
                ans=max(ans,mx);
            }
        now=R;
        int cntt=1,ll=1,rr=0;
        memset(q,-0x3f,sizeof(q));
        while(now)
        {
            if(ll<=rr)
                ans=max(ans,q[ll][0]-cntt+q[ll][1]+dis[now]);
            while(ll<=rr&&dis[now]>=q[ll][0]-cntt+q[ll][1]) ll++;
            q[++rr][0]=dis[now],q[rr][1]=cntt;
            cntt++;
            now=F[now];
        }
    }
    ans+=D;
    printf("%d\n",(n-1<<1)+k-ans);
    return 0;
}

---

2018.6.28