Bellman-Ford&&SPFA

我们前文说过，有关最短路径除了Floyed算法之外，还有许多更加好的方法。这里讲一下有关 Bellman-Ford和SPFA的知识

Bellman-Ford：复杂度O（VE）

有关Bellman-Ford，也不是特别的重要，可以说算是对于SPFA的一个铺垫（有更好的方法还用什么laji更慢的算法呢？）【这里有一个迭代搞的我很懵，这里暂且看做是有关松弛的操作】

Bellman-Ford算法是求含负权图的单源最短路径的一种算法，效率较低，代码难度较小。其原理为连续进行松弛，在每次松弛时把每条边都更新一下，若在n-1次松弛后还能更新，则说明图中有负环，因此无法得出结果，否则就完成。

从这里大家可以看出Bellman-Ford和SPFA在一定程度上的弊端：图中有负环则无法出答案。但可以对其进行一步判断

我们应当明确一点：Bellman-Ford算法是用来解决单源最短路问题的。（恩，没毛病）

这里需要进行多次的松弛操作，每一次成功的松弛操作，都意味着我们发现了一条新的最短路。所以这个方法显然是对的，但是显然laji够慢

(下面这一段是黈的，毕竟本蒟蒻不会迭代QAQ)

注意：1.只有上一次迭代中松弛过的点才有可能参与下一次迭代的松弛操作。

　　　2.迭代的实际意义：每次迭代k中，我们找到了经历了k条边的最短路。

　　　3.没有点能够被“松弛”时，迭代结束　　

//由于我不太写Bellman-Ford的代码，这里用的是百度百科的，害怕误人子弟qwq
#include<iostream>
#include<cstdio>
using namespace std;  

#define MAX 0x3f3f3f3f
#define N 1010
int nodenum, edgenum, original; //点，边，起点  

typedef struct Edge //边
{
    int u, v;
    int cost;
}Edge;  

Edge edge[N];
int dis[N], pre[N];  

bool Bellman_Ford()
{
    for(int i = ; i <= nodenum; ++i) //初始化
        dis[i] = (i == original ?  : MAX);
    for(int i = ; i <= nodenum - ; ++i)
        for(int j = ; j <= edgenum; ++j)
            if(dis[edge[j].v] > dis[edge[j].u] + edge[j].cost) //松弛（顺序一定不能反~）
            {
                dis[edge[j].v] = dis[edge[j].u] + edge[j].cost;
                pre[edge[j].v] = edge[j].u;
            }
    bool flag = ; //判断是否含有负权回路
    for(int i = ; i <= edgenum; ++i)
        if(dis[edge[i].v] > dis[edge[i].u] + edge[i].cost)
        {
            flag = ;
            break;
        }
        return flag;
}  

void print_path(int root) //打印最短路的路径（反向）
{
    while(root != pre[root]) //前驱
    {
        printf("%d-->", root);
        root = pre[root];
    }
    if(root == pre[root])
        printf("%d\n", root);
}  

int main()
{
    scanf("%d%d%d", &nodenum, &edgenum, &original);
    pre[original] = original;
    for(int i = ; i <= edgenum; ++i)
    {
        scanf("%d%d%d", &edge[i].u, &edge[i].v, &edge[i].cost);
    }
    if(Bellman_Ford())
        for(int i = ; i <= nodenum; ++i) //每个点最短路
        {
            printf("%d\n", dis[i]);
            printf("Path:");
            print_path(i);
        }
    else
        printf("have negative circle\n");
    return ;
}  

SPFA：复杂度O（MN）【这里的M在一般不毒瘤的题里是2，N就是边数】

SPFA 算法是 Bellman-Ford算法的队列优化算法的别称，通常用于求含负权边的单源最短路径，以及判负权环。SPFA 最坏情况下复杂度和朴素 Bellman-Ford 相同，为 O(VE)。

相对于Dijkstra算法来说有相似之处，但又不同（貌似Dijkstra更稳一些qwq）

算法大致流程是用一个队列来进行维护。 初始时将源加入队列。 每次从队列中取出一个元素，并对所有与他相邻的点进行松弛，若某个相邻的点松弛成功，则将其入队。 直到队列为空时算法结束。

这样就可以大幅度的减少复杂度（毒瘤题除外）

因为本蒟蒻初学，这里发一个简单的代码

可以过洛谷P3371 【模板】单源最短路径（弱化版）

题目描述

如题，给出一个有向图，请输出从某一点出发到所有点的最短路径长度。

输入输出格式

输入格式：

第一行包含三个整数N、M、S，分别表示点的个数、有向边的个数、出发点的编号。

接下来M行每行包含三个整数Fi、Gi、Wi，分别表示第i条有向边的出发点、目标点和长度。

输出格式：

一行，包含N个用空格分隔的整数，其中第i个整数表示从点S出发到点i的最短路径长度（若S=i则最短路径长度为0，若从点S无法到达点i，则最短路径长度为2147483647）

输入输出样例

输入样例#1：
复制

4 6 1
1 2 2
2 3 2
2 4 1
1 3 5
3 4 3
1 4 4

输出样例#1： 复制

0 2 4 3

说明

时空限制：1000ms,128M

数据规模：

对于20%的数据：N<=5，M<=15；

对于40%的数据：N<=100，M<=10000；

对于70%的数据：N<=1000，M<=100000；

对于100%的数据：N<=10000，M<=500000。保证数据随机。

对于真正 100% 的数据，请移步P4779。请注意，该题与本题数据范围略有不同。

样例说明：

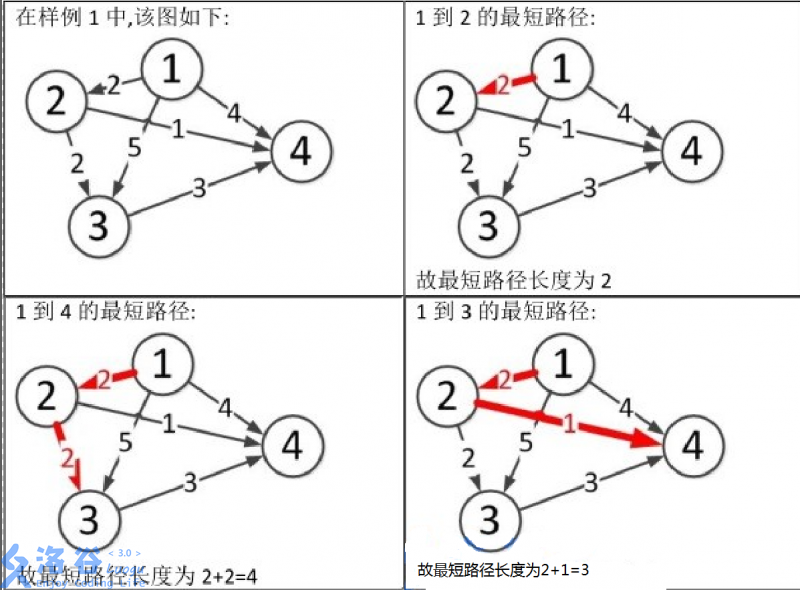
图片1到3和1到4的文字位置调换

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<queue>

using namespace std;

const int inf=;

int n,m,s;
int dis[],vis[],head[],num_edge;

struct Edge{
    int next,to,dis;
}edge[];

queue <int> q;

void addedge(int from,int to,int dis)
{
    num_edge++;
    edge[num_edge].next=head[from];
    edge[num_edge].to=to;
    edge[num_edge].dis=dis;
    head[from]=num_edge;
}

void spfa()
{
    for(int i=;i<=n;++i)
    {
        dis[i]=inf;
        vis[i]=;
    }
    dis[s]=;
    vis[s]=;
    q.push(s);
    while(!q.empty())
    {
        int u=q.front();
        q.pop();
        vis[u]=;
        for(int i=head[u];i;i=edge[i].next)
        {
            int v=edge[i].to;
            if(dis[v]>dis[u]+edge[i].dis)
            {
                dis[v]=dis[u]+edge[i].dis;
                if(!vis[v])
                {
                    q.push(v);
                    vis[v]=;
                }
            }
        }
    }
}

int main()
{
    scanf("%d %d %d",&n,&m,&s);
    for(int i=;i<=m;++i)
    {
        int u,v,d;
        scanf("%d %d %d",&u,&v,&d);
        addedge(u,v,d);
    }
    spfa();
    for(int i=;i<=n;++i)
    {
        if(i==s) printf("0 ");
        else printf("%d ",dis[i]);
    }
    return ;
}