洛谷P1397 [NOI2013]矩阵游戏

矩阵快速幂+费马小定理

矩阵也是可以跑费马小定理的，但是要注意这个：

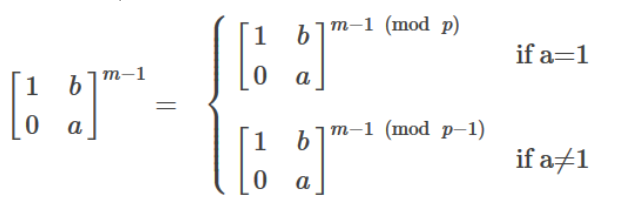
(图是盗来的QAQ)

就是说如果矩阵a[i][i]都是相等的，那么就是mod p 而不是mod p-1了

#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<cstring>
#include<vector>
#include<cmath>
#define MOD 1000000007
#define MAXN 1000000+10
#define ll long long
#define pb push_back
#define ft first
#define sc second
#define mp make_pair
using namespace std;
char s1[MAXN],s2[MAXN];
int n,m;
int a,b,c,d,p;
struct Mat{
    int a[2][2];
    Mat(){
        memset(a,0,sizeof(a));
    }
    friend Mat operator * (const Mat &A,const Mat B){
        Mat C;
        for(int i=0;i<2;i++){
            for(int j=0;j<2;j++){
                for(int k=0;k<2;k++){
                    C.a[i][j]+=(1LL*A.a[i][k]*B.a[k][j]%MOD);
                    C.a[i][j]%=MOD;
                }    
            }    
        }    
        return C;
    }
    friend Mat operator ^ (Mat A,int p){
        Mat B;
        B.a[0][0]=B.a[1][1]=1;
        while(p){
            if(p&1){
                B=B*A;
            }    
            A=A*A;
            p>>=1;
        }
        return B;
    }
};
void solve(){
    scanf("%s%s",s1+1,s2+1);
    scanf("%d%d%d%d",&a,&b,&c,&d);
    p=MOD-1+(a==1);
    int len=strlen(s2+1);
    for(int i=1;i<=len;i++){
        m=(1LL*m*10+s2[i]-'0')%p;
    }
    m--;if(m<0)m+=p;
    Mat A;
    A.a[0][0]=a,A.a[0][1]=b,A.a[1][1]=1;
    Mat B;
    B=A^m;
    Mat C;
    C=B;
    A.a[0][0]=c,A.a[0][1]=d,A.a[1][1]=1;
    C=C*A;
    p=MOD-1+(C.a[0][0]==C.a[1][1]);
    len=strlen(s1+1);
    for(int i=1;i<=len;i++){
        n=(1LL*n*10+s1[i]-'0')%p;
    }
    n--;if(n<0)n+=p;
    C=C^n;
    C=C*B;
    int ans=(C.a[0][0]+C.a[0][1])%MOD;
    printf("%d\n",ans);
}
int main()
{
    //freopen("data.in","r",stdin);
    solve();
    return 0;
}