[SDOI2009]虔诚的墓主人

题目描述

小W是一片新造公墓的管理人。公墓可以看成一块N×M的矩形，矩形的每个格点，要么种着一棵常青树，要么是一块还没有归属的墓地。

当地的居民都是非常虔诚的基督徒，他们愿意提前为自己找一块合适墓地。为了体现自己对主的真诚，他们希望自己的墓地拥有着较高的虔诚度。

一块墓地的虔诚度是指以这块墓地为中心的十字架的数目。一个十字架可以看成中间是墓地，墓地的正上、正下、正左、正右都有恰好k棵常青树。

小W希望知道他所管理的这片公墓中所有墓地的虔诚度总和是多少。

输入输出格式

输入格式：

输入文件religious.in的第一行包含两个用空格分隔的正整数N和M，表示公墓的宽和长，因此这个矩形公墓共有(N+1) ×(M+1)个格点，左下角的坐标为(0, 0)，右上角的坐标为(N, M)。

第二行包含一个正整数W，表示公墓中常青树的个数。

第三行起共W行，每行包含两个用空格分隔的非负整数xi和yi，表示一棵常青树的坐标。输入保证没有两棵常青树拥有相同的坐标。

最后一行包含一个正整数k，意义如题目所示。

输出格式：

输出文件religious.out仅包含一个非负整数，表示这片公墓中所有墓地的虔诚度总和。为了方便起见，答案对2,147,483,648取模。

输入输出样例

输入样例#1：
复制

输出样例#1： 复制

说明

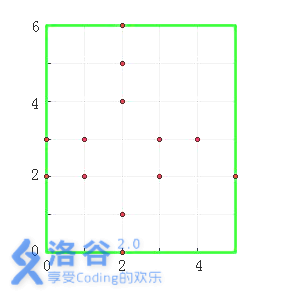
图中，以墓地(2, 2)和(2, 3)为中心的十字架各有3个，即它们的虔诚度均为3。其他墓

地的虔诚度为0。

对于30%的数据，满足1 ≤ N, M ≤ 1,000。

对于60%的数据，满足1 ≤ N, M ≤ 1,000,000。

对于100%的数据，满足1 ≤ N, M ≤ 1,000,000,000，0 ≤ xi ≤ N，0 ≤ yi ≤ M，1 ≤ W ≤ 100,000，1 ≤ k ≤ 10。

存在50%的数据，满足1 ≤ k ≤ 2。

存在25%的数据，满足1 ≤ W ≤ 10000。

对于一个墓地,以它为中心的十字架的个数为

$C_l^{k}*C_r^{k}*C_u^{k}*C_d^{k}$

$l,r,u,d$分别表示四个方向的树的数量

先离散，按x第一关键词，y为第二关键词排序

枚举x坐标相同的两个点，然后树状数组维护两个点之间的

$C_l^{k}*C_r^{k}$

 #include<iostream>

 #include<cstdio>

 #include<cmath>

 #include<algorithm>

 #include<cstring>

 using namespace std;

 typedef long long lol;

 const int N=3e5;

 struct Node

 {

   lol x,y;

 }a[N+],p[N+];

 lol Mod=;

 lol num,n,k,R,C;

 lol c[N+],b[N+],Co[N+][],r[N+],l[N+],ans;

 bool cmp(Node a,Node b)

 {

   if (a.x==b.x)

     return a.y<b.y;

   return a.x<b.x;

 }

 void add(int x,lol d)

 {

   while (x<=num)

     {

       c[x]+=d;

       c[x]%=Mod;

       x+=(x&(-x));

     }

 }

 lol query(int x)

 {

   lol s=;

   while (x)

     {

       s+=c[x];

       s%=Mod;

       x-=(x&(-x));

     }

   return s;

 }

 int main()

 {int i,j,ed,cnt;

   cin>>R>>C;

   cin>>n;

   for (i=;i<=n;i++)

     {

       scanf("%lld%lld",&a[i].x,&a[i].y);

       b[++num]=a[i].x;b[++num]=a[i].y;

     }

   cin>>k;

   sort(b+,b+num+);

   num=unique(b+,b+num+)-b-;

   for (i=;i<=n;i++)

     {

       a[i].x=lower_bound(b+,b+num+,a[i].x)-b;

       a[i].y=lower_bound(b+,b+num+,a[i].y)-b;

     }

   sort(a+,a+n+,cmp);

   Co[][]=Co[][]=;

   for (i=;i<=;i++)

     {

       Co[i][]=;

       for (j=;j<=min(,i);j++)

     {

       Co[i][j]=(Co[i-][j-]+Co[i-][j])%Mod;

     }

     }

   for (i=;i<=n;i++)

     r[a[i].y]++;

   for (i=;i<=n;i=ed+)

     {

       ed=i;cnt=;

       p[++cnt]=a[i];

       while (ed+<=n&&(a[ed+].x==a[ed].x)) p[++cnt]=a[ed+],ed++;

       for (j=;j<=cnt;j++)

     {

       lol y=p[j].y;

       add(y,(Co[l[y]+][k]*Co[r[y]-][k]%Mod-Co[l[y]][k]*Co[r[y]][k]%Mod+Mod)%Mod);

       l[y]++;r[y]--;

       if (j>k&&cnt-j+>=k)

         ans+=Co[j-][k]*Co[cnt-j+][k]%Mod*((query(y-)-query(p[j-].y)+Mod)%Mod)%Mod;

       ans%=Mod;

     }

     }

   cout<<ans;

 }