6. B树

一、B 树是一种多叉平衡查找树

相较于二叉结构的红黑树，B 树是多叉结构，所以在元素数量非常多的情况下，B 树的高度不会像二叉树那么大，从而保证查询效率。

一棵含 n 个结点的 B 树的高度 h = O(log_tn)，其中 t 是 B 树的最小度数。

• 提出多叉平衡查找树的思维历程：查询效率要更高 ----> 查询次数要更少 ----> 查找树的高度要更低 ----> 每个结点保存的信息要更多 ----> 多叉

下图是一棵B树的示意图：

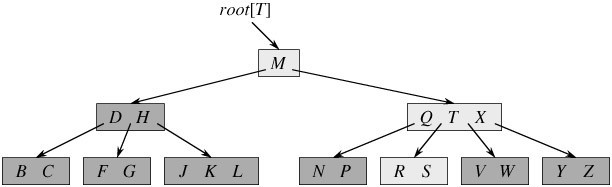
二、B 树的定义

《算法导论》中用最小度数 t 来定义 B 树，所谓最小度数，即结点拥有的最小孩子数。

一棵最小度数为 t 的 B 树是满足如下四个条件：

1. 每个非根结点至少含有 t - 1 个关键字，根结点至少含有 1 个关键字
2. 每个结点至多含有 2t - 1 个关键字，即一个结点至多可有 2t 个孩子（如果一个结点恰好有 2t - 1 个关键字，我们就说这个结点是满的）
3. 一个结点 u 中的关键字按非降序排列，如u.key₁ ≤ u.key₂ ≤ … ≤ u.key_n-1
4. 每个节点的关键字对其子树的范围分割，设节点 u 有 n + 1 个指针，指向其 n + 1 棵子树，指针为u.p₀, u.p₁, u.p₂, …, u.p_n，关键字 k_i 为 u.p_i 所指的子树中的关键字，有 k₀ ≤ u.key₀ ≤ k₁ ≤ u.key₁ … ≤ u.key_n-1 ≤ k_n 成立
5. 所有叶子结点具有相同的深度，即树的高度 h（这表明了 B 树是平衡的）

/* B树结点结构 */
struct BTreeNode {
	int keyNum;				// 关键字的数目
	BTreeNode *parent;		// 指向父结点
	BTreeNode **ptr;		// 子树指针向量：ptr[0]...ptr[keyNum]
	KeyType *key;			//  关键字向量；key[0]...key[keyNum-1]
}; 

三、查询操作

例题：一棵已经建立好的B树如下图所示，要求查找关键字为29的文件。

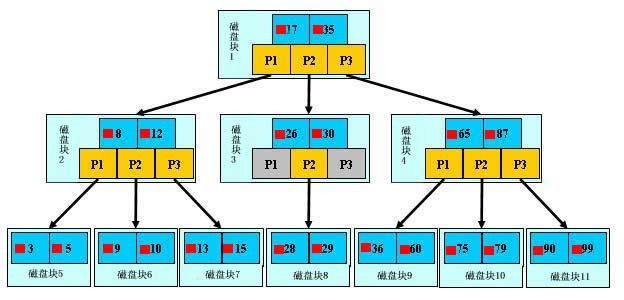
• 结点中的关键字表示磁盘文件的文件名，而小红块表示对应的关键字所代表的文件在硬盘中的存储位置，P是指针

• 指针、关键字以及关键字所代表的文件地址合起来构成了B树的一个结点，这个结点存储在一个磁盘块上

• 假如每个磁盘块正好可以存放一个B树的结点（正好存放2个文件名）。那么一个B树结点就代表一个盘块，而子树指针就是存放另外一个盘块的地址

搜索过程如下：

1. 从根结点开始，读取根结点信息，根结点有2个关键字：17和35。因为17 < 29 < 35，所以找到指针P2指向的子树，也就是磁盘块3（1次I/0操作）

2. 读取当前结点信息，当前结点有2个关键字：26和30。因为26 < 29 < 30，所以找到指针P2指向的子树，也就是磁盘块8（2次I/0操作）

3. 读取当前结点信息，当前结点有2个关键字：28和29。找到了！（3次I/0操作）

由上面的过程可见，同样的操作，如果使用平衡二叉树，那么需要至少4次 I/O 操作，而且这种优势还会随着结点数的增加而更加明显。另外，因为 B 树结点中的关键字都是排好序的，所以，在结点中的信息被读入内存之后，可以采用二分查找这种快速的查找方式，更进一步减少了读入内存之后的计算时间。由此可见，对于外存数据结构来说，I/O操作的次数是其查找信息中最大的时间消耗，而我们要做的所有努力就是尽量在搜索过程中减少I/O操作的次数。

如何理解“树的高度过大而造成磁盘I/O读写过于频繁，进而导致查询效率低下”这句话？

在大规模数据存储方面，大量数据存储在外存磁盘中，而在外存磁盘中读取/写入块（block）中某数据时，首先需要定位到磁盘中的某磁盘块。

磁盘读取数据是以盘块（block）为基本单位的。位于同一盘块中的所有数据都能被一次性全部读取出来。而磁盘I/O代价主要花费在盘块查找时间T上。因此我们应该尽量将相关信息存放在同一盘块，同一磁道中。或者至少放在同一柱面或相邻柱面上，以求在读/写信息时尽量减少磁头来回移动的次数，避免过多的查找时间T。

因此，使用B树使得树的高度更低，从而需要查找的盘块也就更少（即减少磁盘I/O操作的次数），所需的盘块查找时间也就越低，查询效率自然提高。

四、插入/删除操作

参考博客：B树&B+树、B树与B+树