图论——最短路径 Dijkstra算法、Floyd算法

1.弗洛伊德算法（Floyd）

弗洛伊算法核心就是三重循环，M [ j ] [ k ] 表示从 j 到 k 的路径，而 i 表示当前 j 到 k 可以借助的点；红色部分表示，如果 j 到 i ，i 到 k 是通的，就将 j 到 k 的值更新为

M[j][i] + M[i][k] 和 M[j][k] 较短的一个。

<<;

; i <= n; i++) {
        ; j <= n; j++) {
            ; k <= n; k++) {
                if (j!=k) {
                        M[j][k] = min(M[j][i] + M[i][k] , M[j][k]);
                }
            }
        }
}

给个题目链接，写完可以交试一下：http://www.dotcpp.com/oj/problem1709.html

完整代码：

#include <iostream>
#include <queue>
using namespace std;

#define inf 2147483647
][];

int main() {
    int n;
    queue<int>q;
    cin >> n;
    ; i <= n; i++) {
        ; j <= n; j++) {
            cin >> M[i][j];
             && i != j)M[i][j] = inf;
        }
    }
    ; i <= n; i++) {
        ; j <= n; j++) {
            ; k <= n; k++) {
                ) {
                    if (M[j][i] != inf && M[i][k] != inf) {
                        M[j][k] = M[j][i] + M[i][k] < M[j][k] ? M[j][i] + M[i][k] : M[j][k];
                    }
                }
            }
        }
    }

    ; i <= n; i++) {
        ; j <= n; j++) {
             << " ";
            else
            cout << M[i][j] << " ";
        }
        cout << endl;
    }

    ;
}

2.迪杰斯特拉

Floyd只要暴力的三个for就可以出来，代码很好理解，但缺点就是时间复杂度高是O(n³)。Dijkstra的时间复杂度是O(n²)，要快很多。

不过要注意这个算法所求的是单源最短路。所以说，如果题目是求任意一对顶点间的最短路径问题，那就需要对每个顶点进行一遍迪杰斯特拉算法，这种情况就适合弗洛伊德算法了。

思想图解：

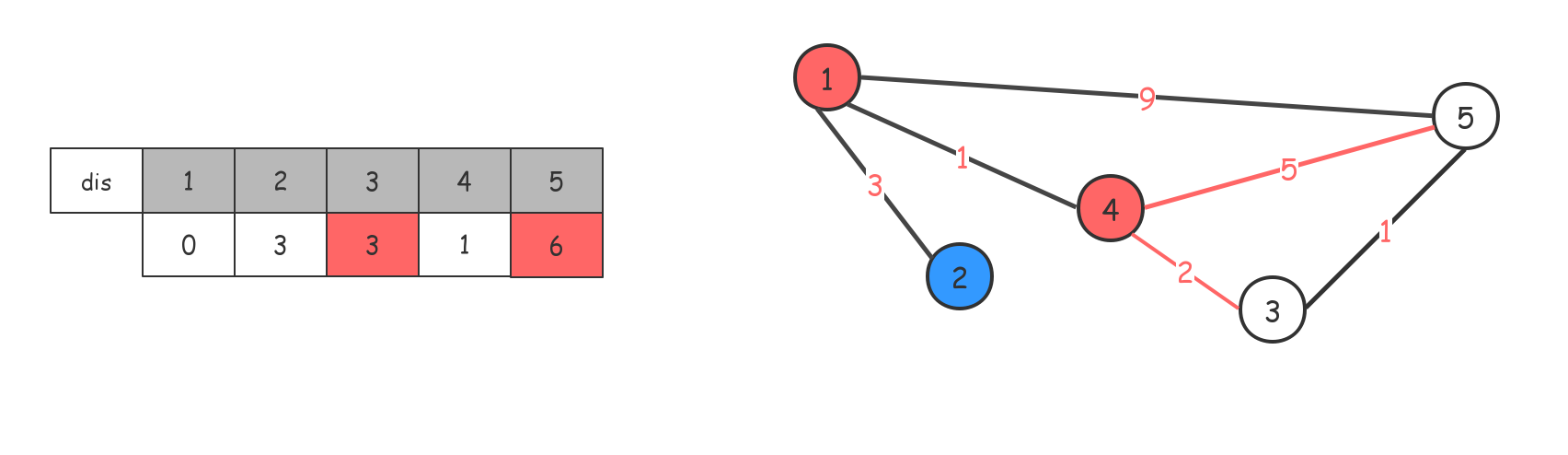
用dis数组实时记录起始点（起始点取1） 到达的所有节点的距离。（自己到自己的路径长度 0，到不了的点是 inf（极大值））

dis数组初始值是这样的，4是当前距离节点1最近的点。（已经访问过的，我们标记上不再次访问）

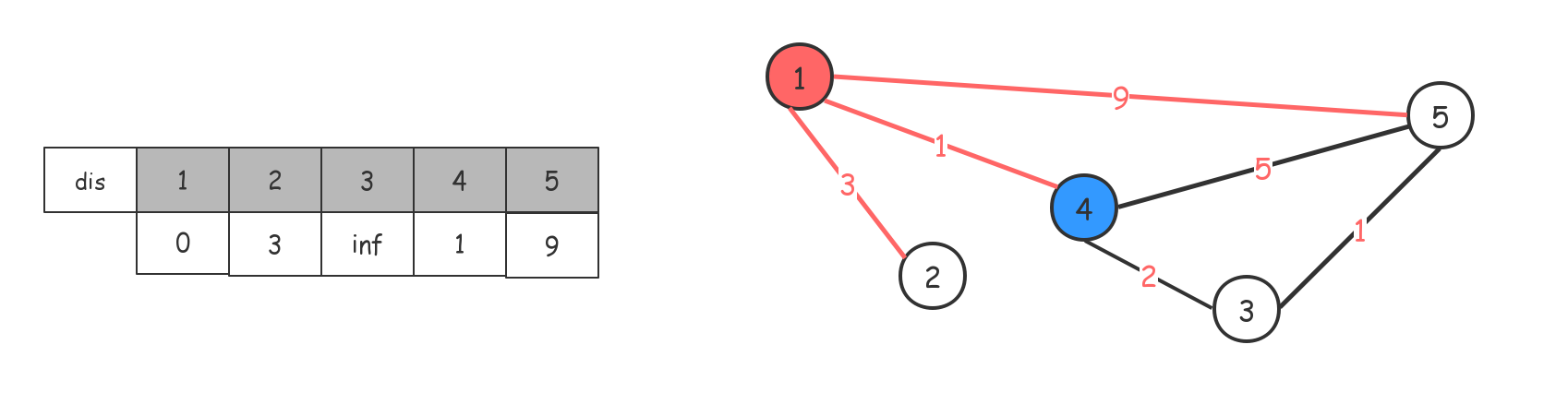
借助4节点，对dis数组进行更新（如果有更短的路径，就对dis数组进行值替换），走到2，无操作。

借助3节点，对dis数组进行更新，最后走到5节点，退出。（实际过程中，走到最后一个节点，别的节点都访问过，进行标记了，什么也不会做）。

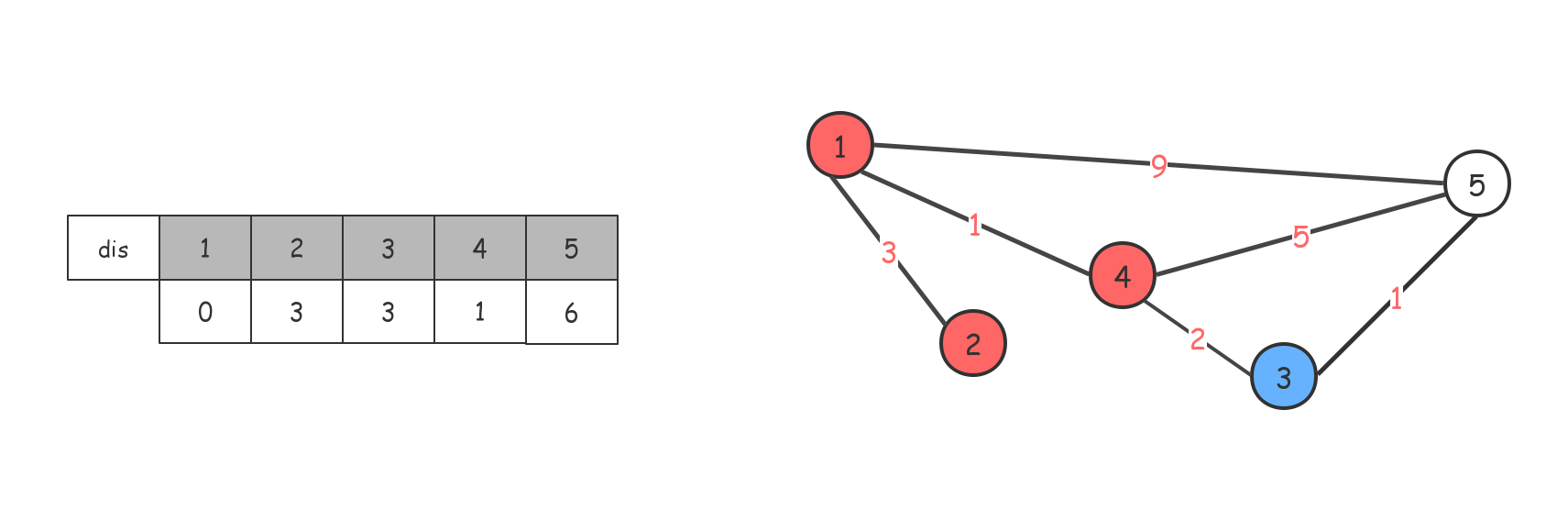
借助3节点，对dis数组进行更新

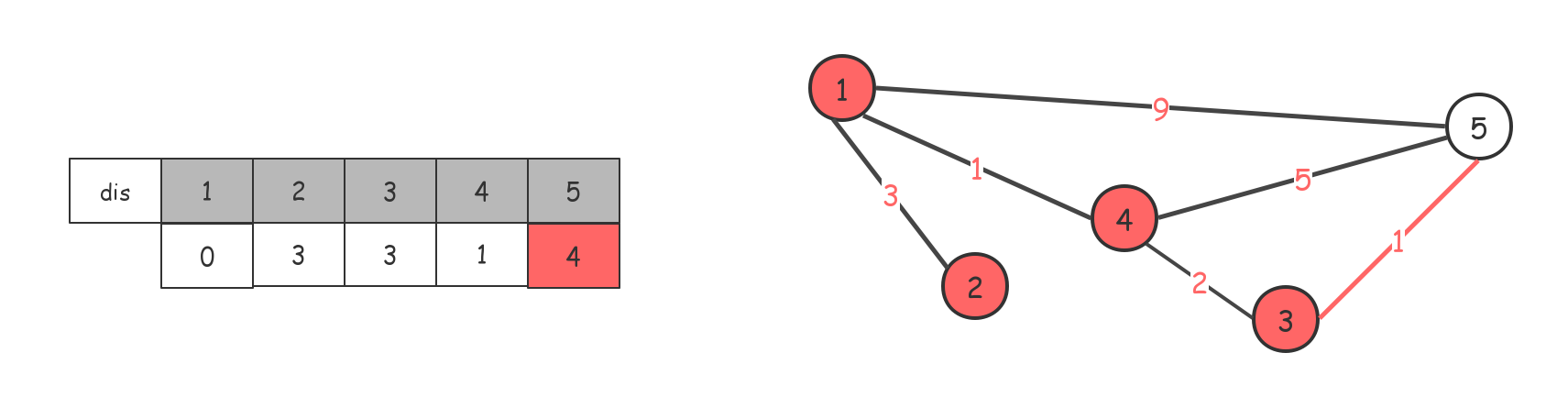
测试题目：http://acm.hdu.edu.cn/showproblem.php?pid=2544 （数据很弱，AC了，实现也不一定是正确的，强烈建议再做后面一题）

#include <iostream>
#include <algorithm>
#include <string.h>
using namespace std;

 << ;
int n, m;
];
][];
];

void initialize() {
    memset(book, , sizeof(book));
    ; i <= n; i++) {
        ; j <= n; j++) {
            if (i != j)M[i][j] = inf;
        }
    }
}
void dijkstra() {
    while (true) {
        ;
        ; i <= n; i++) {
             || dis[i] < dis[v])) v = i;//从dis数组中找出当前距离起点最短的节点
        }
        ) break;
        book[v] = true;
        ; i <= n; i++) {
            dis[i] = min(dis[i], dis[v] + M[v][i]);
        }
    }
}
int main() {
    while (cin >> n >> m) {
         && m == )break;
        initialize();
        ; i < m; i++) {
            int A, B, C;
            cin >> A >> B >> C;
            M[A][B] = C;
            M[B][A] = C;
        }
        book[] = true;
        ; i <= n; i++) {
            dis[i] = M[][i];
        }
        dijkstra();

        cout << dis[n] << endl;
    }
    ;
}

使用优先级队列优化查找过程（理论上是要更快的，但是我交上去，时间反而更慢了）：

#include <iostream>
#include <queue>
#include <algorithm>
using namespace std;

 << ;
int n, m;

][];
];

class Node {
public:
    int to,distance;
    Node(int t, int d) {
        to = t; distance = d;
    }
    bool operator< (Node a) const{
        return a.distance < distance;
    }
};

priority_queue<Node>q;
void initialize() {
    ; i <= n; i++) {
        ; j <= n; j++) {
            if (i != j)M[i][j] = inf;
        }
    }
}
void dijkstra() {
    while (!q.empty()) {
        int min; min = q.top().to;q.pop();
        //处理掉之前push进去的，距离较长的边，不写不会错，效率会降低。
        while (!q.empty() && q.top().to == min) {
            q.pop();
        }
        ; i <= n; i++) {
            if (dis[i] > dis[min] + M[min][i]) {
                dis[i] = dis[min] + M[min][i];
                q.push(Node(i, dis[i]));
            }
        }
    }
}

int main() {
    while (cin >> n >> m) {
         && m == )break;
        initialize();
        ; i < m; i++) {
            int A, B, C;
            cin >> A >> B >> C;
            M[A][B] = C;
            M[B][A] = C;
        }
        ; i <= n; i++) {
            dis[i] = M[][i];
             && dis[i] != inf) {
                q.push(Node(i, dis[i]));
            }
        }
        dijkstra();
        cout << dis[n] << endl;
    }
    ;
}

邻接表+优先级队列：（邻接表的迪杰斯特拉实现起来，要复杂得多，但是跑起来确实比较快）

#include <iostream>
#include <stdio.h>
#include <queue>
using namespace std;
];
 << ;
];
class ENode {
public:
    int to;
    int dis;
    ENode *next = NULL;
    ENode() {};
    ENode(int t, int d) {
        dis = d; to = t;
    }

    void push(int t, int d) {
        ENode *p = new ENode;
        p->to = t; p->dis = d;
        p->next = next;
        next = p;
    }

    bool operator<(ENode e)const {
        return e.dis < dis;
    }
}head[];

int main() {
    priority_queue<ENode>q;
    int n, m, c1, c2, c3;
    while (cin >> n >> m) {
         && m == )break;
        ; i <= n; i++) {
            dis[i] = inf;
            fuck[i] = false;
        }
        ; i < m; i++) {
            scanf("%d%d%d", &c1, &c2, &c3);
            head[c1].push(c2, c3);
            head[c2].push(c1, c3);
             || c2 == ) {
                dis[c1 ==  ? c2 : c1] = c3;
                q.push(*head[c1].next);
            }
        }
        fuck[] = true;

        while (!q.empty()) {
            int fm = q.top().to; q.pop();
            if (fuck[fm])continue;
            fuck[fm] = true;
            ENode *p = head[fm].next;
            while (p) {
                int me = p->to;
                if (dis[me] > dis[fm] + p->dis) {
                    dis[me] = dis[fm] + p->dis;
                    q.push(ENode(me, dis[me]));
                }
                p = p->next;
            }
        }

        printf("%d\n", dis[n]);
        ; i <= n; i++) {
            ENode *p = head[i].next;
            while (p) {
                ENode *t = p->next;
                delete p;
                p = t;
            }
            head[i].next = NULL;
        }
    }
    ;
}

理解不深刻，实现出来的错误版本，能出来正确的答案，但升高了复杂度：

#include <iostream>
#include <stdio.h>
#include <queue>
using namespace std;
];
];
 << ;

class ENode {
public:
    int to;
    int dis;
    ENode *next = NULL;

    void push(int t, int d) {
        ENode *p = new ENode;;
        p->to = t; p->dis = d;
        p->next = next;
        next = p;
    }

    bool operator<(ENode e)const {
        return e.dis < dis;
    }
}head[];

int main() {
    priority_queue<ENode>q;
    int n, m, c1, c2, c3;
    while (cin >> n >> m) {
         && m == )break;
        ; i <= n; i++) {
            dis[i] = inf;
        }
        ; i < m; i++) {
            scanf("%d%d%d", &c1, &c2, &c3);
            head[c1].push(c2, c3);
            head[c2].push(c1, c3);
        }

        ENode *p = head[].next;
        while (p) {
            q.push(*p);
            dis[p->to] = p->dis;
            p = p->next;
        }

        while (!q.empty()) {
            int fm = q.top().to; q.pop();
            /*------------*/
            /*这个是错误指定背锅店，如果不写这一句，当出现完全图的情况时，
            算法会近乎退化成n^n，HDU的这题测试数据太弱了，导致我没有发现问题。
            写了的话，由于下面往队列中Push的错误的，这里也就成了背锅点*/
            if (fuck[fm])continue;
            fuck[fm] = true;
            /*------------*/
            ENode *p = head[fm].next;
            while (p) {
                int me = p->to;
                if (dis[me] > dis[fm] + p->dis) {
                    dis[me] = dis[fm] + p->dis;
                    //真正错误在这里
                    q.push(*p);
                }
                p = p->next;
            }
        }

        printf("%d\n", dis[n]);
        ; i <= n; i++) {
            ENode *p = head[i].next;
            while (p) {
                ENode *t = p->next;
                delete p;
                p = t;
            }
            head[i].next = NULL;
        }
    }
    ;
}

---

我为什么能发现代码实现的错误，因为我天赋过人，因为这题数据很强，https://www.luogu.org/problemnew/show/P4779 数据量很大，100000个节点，不管是时间还是空间上，不能再用邻接矩阵了；邻接表，如果实现得不恰当也是会超时的，这题如果能AC，那算法实现的肯定是没有问题了。

邻接表+优先级队列：

#include <iostream>
#include <stdio.h>
#include <queue>
using namespace std;
];
];
 << ;

class ENode {
public:
    int to;
    int dis;
    ENode *next = NULL;

    void push(int t, int d) {
        ENode *p = new ENode;;
        p->to = t; p->dis = d;
        p->next = next;
        next = p;
    }

    bool operator<(ENode e)const {
        return e.dis < dis;
    }
}head[];

int main() {
    priority_queue<ENode>q;
    int n, m, s, c1, c2, c3;
    cin >> n >> m >> s;
    ; i < m; i++) {
        //cin >> c1 >> c2 >> c3;
        scanf("%d%d%d", &c1, &c2, &c3);
        head[c1].push(c2, c3);
    }

    ; i <= n; i++) {
        if (i != s) {
            dis[i] = inf;
        }
    }

    ENode *p = head[s].next;
    while (p) {
         || (p->dis < dis[p->to])) {
            q.push(*p);
            dis[p->to] = p->dis;
        }
        p = p->next;
    }

    while (!q.empty()) {
        //获得当期距离 源点 最近的点
        int min = q.top().to; q.pop();
        if (fuck[min])continue;
        fuck[min] = true;
        ENode *p = head[min].next;
        while (p) {
            int to = p->to;
            if (dis[to] > dis[min] + p->dis) {
                dis[to] = dis[min] + p->dis;
                ENode e = *p;
                e.dis = dis[to];
                q.push(e);
            }
            p = p->next;
        }
    }

    ; i <= n; i++) {
        printf("%d ", dis[i]);
    }
    cout << endl;
    ;
}

3、Bellman-Ford算法

Bellman - ford效率较低，代码难度较小。重要的是若给定的图存在负权边，Dijkstra算法便没有了用武之地，Bellman - ford算法便派上用场了。