UVALive3720

题目大意：见刘汝佳《算法竞赛入门经典——训练指南》P173。

解题思路：

　　问题可以转化为求共有多少条过点阵中的点的斜线。其中必定包含左斜线和右斜线，由于点阵式对称的，所以我们只需求出左右斜线中的一种的总数，乘2就可以得到答案。

　　我们先求出各点到其左上角的只经过两个点的左斜线的总数 cnt ，那么答案就是所有点的 cnt 的总和去掉其中重复计算的数值。设点阵上某点坐标为（i,j），则这个子问题可以转化为求 [ 1,i ] 和 [ 1,j ] 中互质的数对的个数。简单解释：对于点（i,j），若 gcd（i,j）=1，则该点到（0,0）的直线必定只经过此二点；否则你必定可以找到 x=i/gcd（i,j），y=j/gcd（i,j），（i,j）到（0,0）的直线经过（x,y）。而对于该点到左上角其他点（除了（0,0））的只经过两个点的直线，可以通过 [ 1,i ） 和 [ 1,j ）中各点到（0,0）的只经过两个点的直线平移得到（如图1所示）。递推式为：cnt[i][j] = cnt[i-1][j] + cnt[i][j-1] - cnt[i-1][j-1] + （gcd（i,j）==1?1:0）。

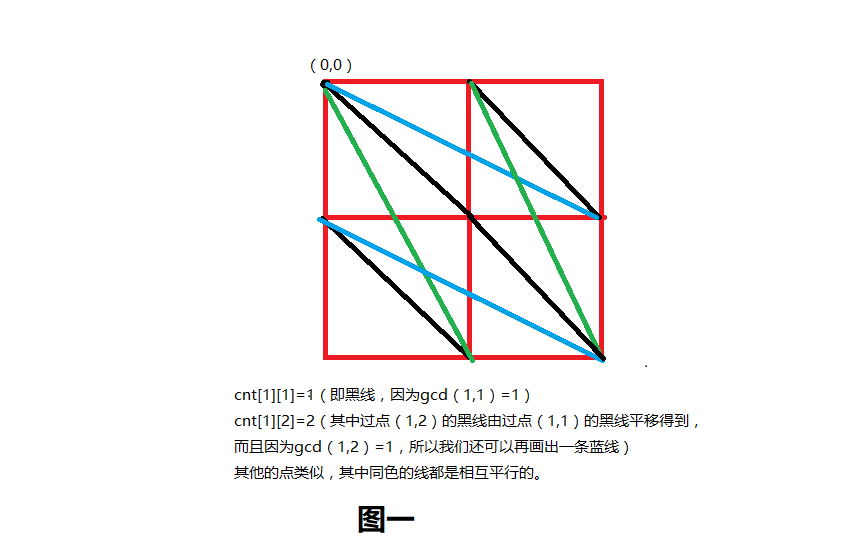
　　现在来算最终答案 ans 。很自然的得出：ans[i][j] = ans[i-1][j] + ans[i][j-1] - ans[i-1][j-1] + cnt[i][j]。但这么计算会有一个重复：在 cnt[i][j] 中包含了 cnt[i/2][j/2] ，所以要再减去 cnt[i/2][j/2]。over.

AC代码：

 #include <cstdio>
 using namespace std;
 const int maxn=;
 int cnt[maxn][maxn],ans[maxn][maxn];
 int gcd(int a,int b){
     if (b == )    return a;
     return gcd(b, a%b);
 }
 void init(){
     for(int i=;i<maxn;i++){
         for(int j=;j<maxn;j++){
             cnt[i][j]=cnt[i-][j]+cnt[i][j-]-cnt[i-][j-]+(gcd(i,j)==?:);
         }
     }
     for(int i=;i<maxn;i++){
         for(int j=;j<maxn;j++){
             ans[i][j]=ans[i-][j]+ans[i][j-]-ans[i-][j-]+cnt[i][j]-cnt[i/][j/];
         }
     }
 }
 int main(){
     init();
     int n,m;
     while(scanf("%d%d",&n,&m)==&&n&&m){
         printf("%d\n",ans[n-][m-]*);
     }
     return ;
 }