JZOJ-2019-11-5 B组

T1

给出一二维01矩阵\(f_{i,j}\), 定义点\((x_a, y_a), (x_b, y_b)\)的「距离」为\(max\{|x_a-x_b|， |y_a-y_b|\}\)

求出一矩阵\(w\), 使得\(w_{i,j}\)为\(f\)中所有距点\((i,j)\)「距离」小于等于\(r\)的点权值之和

\(r \leq n \leq 250\)

解法

二维前缀和大力维护即可

T2

一个小岛\(Abstinence\)上的居民非常喜欢一种不含酒精的啤酒，迄今为止这种不含酒精的啤酒只能从波兰进口。但是今年，\(Abstinence\)岛上的一个城市要建一座酿酒厂。所有的城市都坐落于海岸线上，而且它们仅被一条沿着海岸线绕岛一周的公路所连接。酿酒厂的投资商收集了所有城市对这种酒的需求量，即每个城市每天需要多少桶酒。他同时也有一张两个相邻城市之间的距离表。运输上的花费是每桶每英里一元。一天的啤酒运输费用是从酿酒厂将啤酒运送到各个城市所需的费用总和。每天的花费取决于酒厂的位置，投资商希望找到建厂的位置以使每天的运输花费最小。

在输入文件的BRO.IN中的第一行包含一个整数\(n\)， \(5 \leq n \leq 10000\),表示城市的个数，（我们假设城市沿着公路编号，相邻的城市有相邻的编号，城市\(1\)和\(n\)也是相邻的）。以下的\(n\)行，每行有两个被一个空格隔开的非负整数\(z_i\)，\(d_i\)，表示第\(i\)个城市对啤酒的日需求量和该城市沿高速公路到下一个城市的距离。整条公路的长度不超过\(1000000\)英里，每个城市的日需求量不超过\(1000\)桶。

解法

考虑枚举所有点并依次计算答案, 很明显这会超时

考虑对于当前选择建厂点顺时针移动的过程来说, 逆时针到达它的点的个数是单调不下降并且小于等于\(n\)的, 顺时针到达它的点的个数是单调不上升并且大于等于\(0\)的.

换句话说, 一个点在当前选择建厂点定向移动会且仅会被分成两端区间, 使得一段是到达当前选择建厂点最短路是顺时针的, 一段是到达当前选择建厂点最短路是逆时针的.

即每个点的顺逆状态最多只会被更新一次, \(O(n)\)

T3

现在我们在一个平面上画了n个矩形。每一个矩形的两边都与坐标轴相平行，且矩形定点的坐标均为整数。现我们定义满足如下性质的图形为一个块：

• 每一个矩形都是一个块；
• 如果两个块有一段公共的部分，那么这两个块就会形成一个新的块，否则这两个块就是不同的。

示例：
图1中的矩形形成了两个不同的块。
图2中的矩形形成了一个块。

在输入文件PRO.IN的第一行有一个整数\(n\)，\(1 \leq n \leq 7000\)，表示矩形的个数。接下来的n行描述矩形的顶点，每个矩形用四个数来描述：左下顶点坐标\((x,y)\)与右上顶点坐标\((u,vc)\)。每个矩形的坐标都是不超过10000的非负整数。

解法

暴力枚举\(O(n^2)\)个矩形后使用近似\(O(\alpha(n))\)的并查集维护即可, 注意常数

T4

现在我们在一张纸上有一个笛卡尔坐标系。我们考虑在这张纸上用铅笔从左到右画的折线。我们要求任何两个点之间连接的直线段与\(x\)轴的夹角在\(-45°~45°\)之间，一条满足以上条件的折线称之为平坦的折线。假定给出了\(n\)个不同的整点（坐标为整数的点），最少用几条平坦的折线可以覆盖所有的点？

示例:

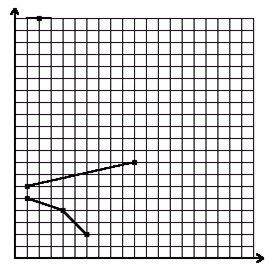
图中有\(6\)个整点：\((1,6), (10,8), (1,5), (2,20), (4,4), (6,2)\)，要覆盖它们至少要\(3\)条平坦的折线。

在输入文件lam.in的第一行有一个正整数\(n\)，不超过\(30000\)，代表点的个数。接下来的\(n\)行表示这些点的坐标，每行有两个用一个空格隔开的整数\(x\),\(y\)，\(0 \leq x \leq 30000\), \(0 \leq y \leq 30000\)。第\(i+1\)行的数字代表第\(i\)个点的坐标。

解法

考虑点\((x_a, y_a), (x_b, y_b)\)可以被连接的充分必要条件: \(|\frac{y_a-y_b}{x_a-x_b}| \leq tan \frac{\pi}{4} (=1)\)

这等价于\(|y_a-y_b| \leq |x_a-x_b|\), 即\(y_b-x_b \leq y_a-x_a\)且\(y_b+x_b \leq y_a+x_a\)

按一维排序另一维贪心即可