HDU 2815 Mod Tree (扩展 Baby Step Giant Step )

Mod Tree

Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)

Total Submission(s): 96 Accepted Submission(s): 38

Problem Description

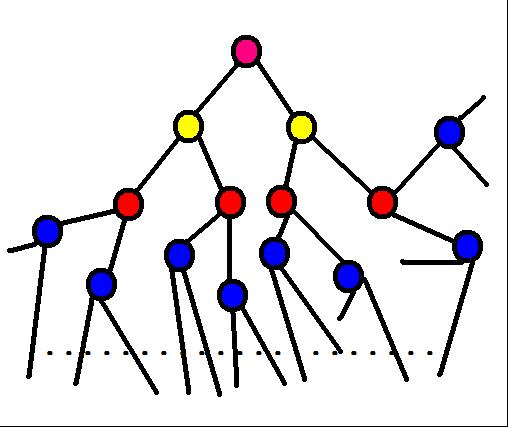  The picture indicates a tree, every node has 2 children.
  The depth of the nodes whose color is blue is 3; the depth of the node whose color is pink is 0.
  Now out problem is so easy, give you a tree that every nodes have K children, you are expected to calculate the minimize depth D so that the number of nodes whose depth is D equals to N after mod P.

 

Input

The input consists of several test cases.
Every cases have only three integers indicating K, P, N. (1<=K, P, N<=10^9)

 

Output

            The minimize D.
If you can’t find such D, just output “Orz,I can’t find D!”

 

Sample Input

3 78992 453
4 1314520 65536
5 1234 67

 

Sample Output

Orz,I can’t find D!
8
20

 

Author

AekdyCoin

证明来自：

http://hi.baidu.com/aekdycoin/item/236937318413c680c2cf29d4

#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
typedef long long LL ;
const int N = ;

struct B
{
    LL num , id ;
    bool operator < ( const B &a ) const{
        if( num != a.num ) return num < a.num;
        else return id < a.id ;
    }
}baby[N];

LL n , k , p ;
int tot ;
void e_gcd( LL &x , LL &y , LL &d , LL a , LL b ){
    if( b ==  ){ x =  , y =  ; d = a ; return ; }
    e_gcd( y , x , d , b , a%b );
    y -= x* (a/b) ;
}

int inv( LL a, LL b ,LL n )
{
    LL d,e,x,y ;
    e_gcd(x,y,d,a,n);
    e = ( x * b ) % n ;
    return e <  ? e + n : e;
}

inline LL gcd(LL a, LL b ){ return b ==  ? a : gcd( b , a % b ) ; }

LL quick_mod( LL a , LL b ,LL mod )
{
    LL res = ;
    while( b )
    {
        if( b & ) res = res * a % mod ;
        a = a * a % mod ;
        b >>=  ;
    }
    return res ;
}

int find( LL n )
{
    int l =  , r = tot -  ;
    while( l <= r ){
        int m = (l + r) >> ;
        if( baby[m].num == n){
            return baby[m].id;
        }
        else if( baby[m].num < n )
            l = m + ;
        else
            r = m -  ;
    }
    return -;
}

void run()
{
    if( p <= n ){
         puts("Orz,I can’t find D!");
         return ;
    }
    LL temp =  % p ;
    for( int i =   ; i <  ; ++i ) {
        if( temp == n ){
                printf("%d\n",i);
                return ;
        }
        temp = temp * k % p ;
    }

    LL d =  , kk =  % p ;
    while( ( temp = gcd( k , p ) ) !=  ){
        if( n % temp ) {
             puts("Orz,I can’t find D!");
             return ;
        }
        d ++ ;
        p /= temp;
        n /= temp;
        kk =  k / temp * kk % p ;
    }
    int m = ( int ) ceil( sqrt( (double)p ) );
    baby[].num =  , baby[].id =  ;
    for( int i =  ; i <= m ; ++i ){
        baby[i].num = baby[i-].num * k % p ;
        baby[i].id = i ;
    }
    sort( baby , baby + m +  ) ;
    tot =  ;
    for( int i =  ; i <= m ; ++i ){
        if(baby[i].num != baby[tot-].num ){
            baby[tot++] = baby[i];
        }
    }

    LL am = quick_mod( k , m , p );

    for( int j =  ; j <= m ; ++j ){
        temp = inv(kk,n,p);
        if( temp <  ){
            continue ;
        }
        int pos = find( temp );
        if( pos != - ){
            printf("%d\n", m * j + d + pos );
            return ;
        }
        kk = kk * am % p    ;
    }
     puts("Orz,I can’t find D!");
}
int main()
{
    #ifdef LOCAL
        freopen("in.txt","r",stdin);
    #endif // LOCAL
    while( scanf("%I64d%I64d%I64d",&k,&p,&n) != EOF ) run();
}