2019.7.26 NOIP 模拟赛

---

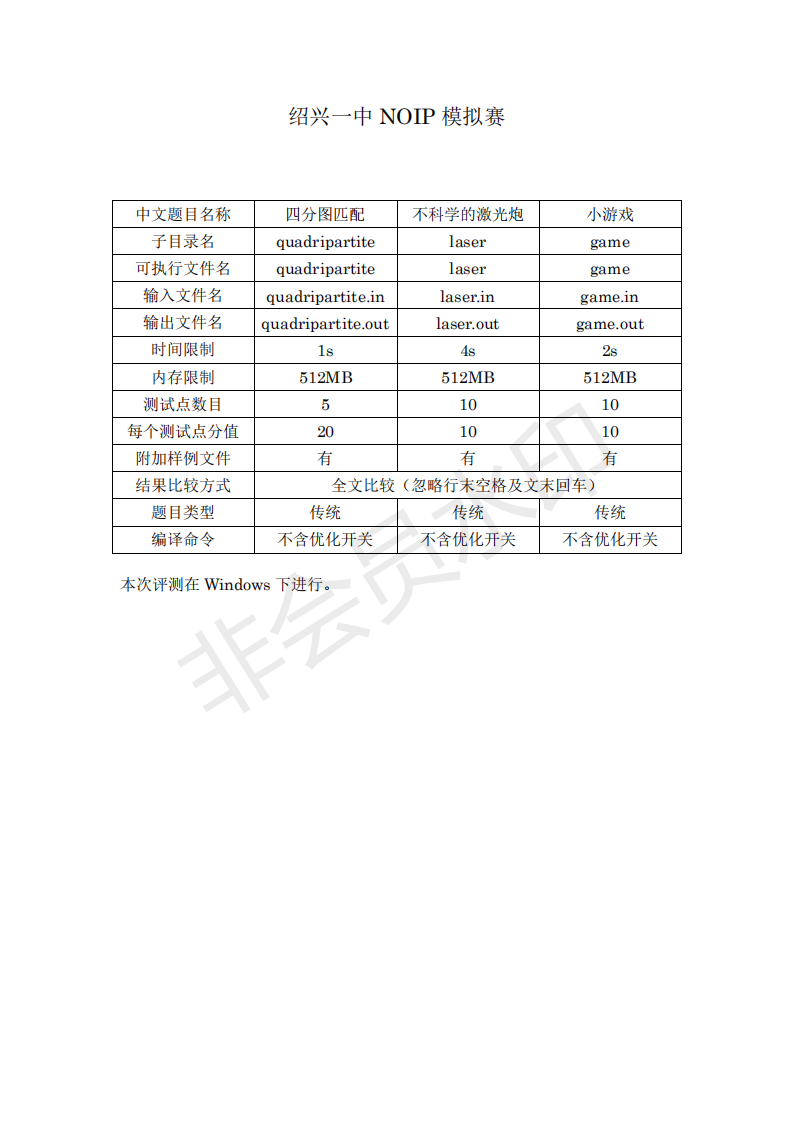
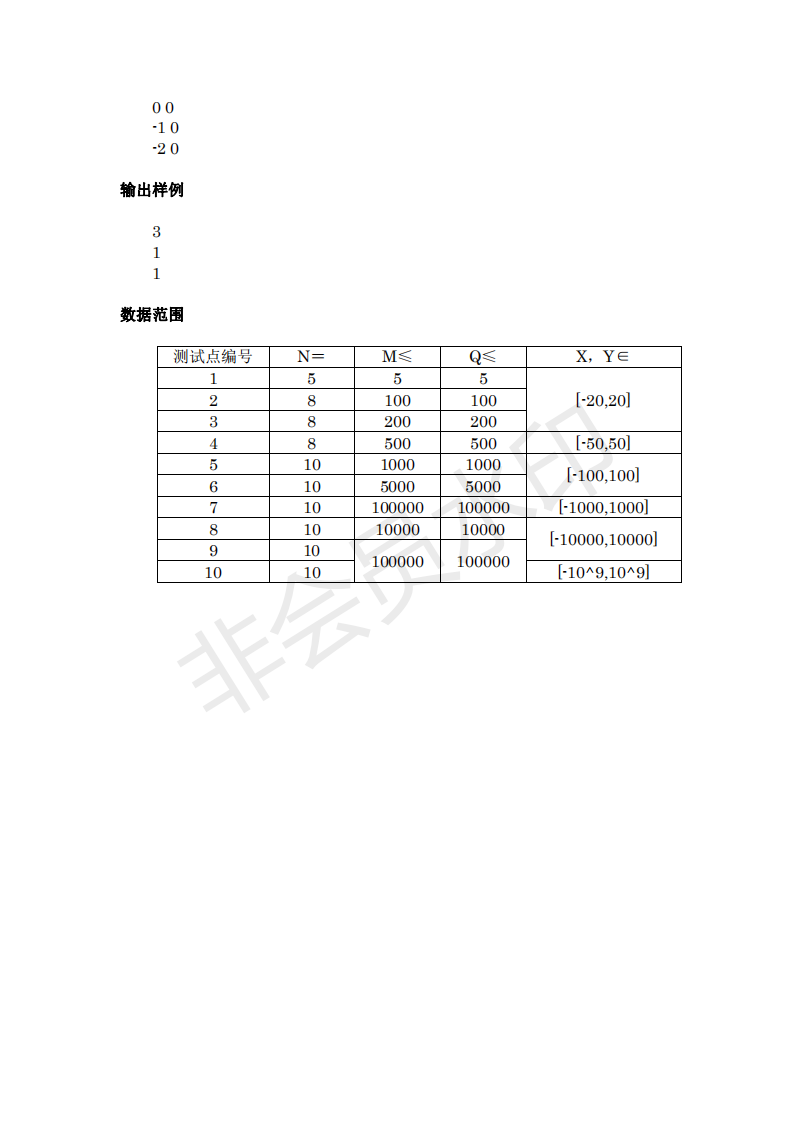
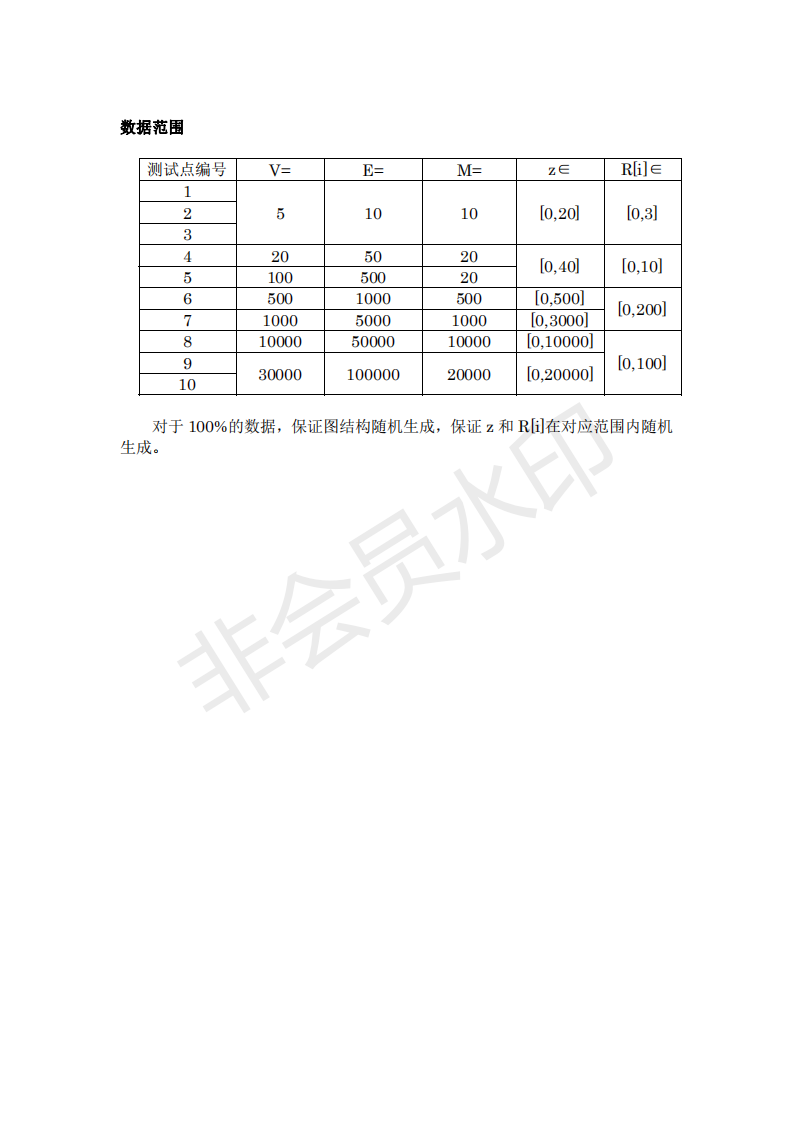
这次模拟赛真的，，卡常赛。

The solution of T1:

std是打表，，考场上sb想自己改进匈牙利然后wei了（好像匈牙利是错的。

大力剪枝搜索。代码不放了。

　　

　　这是什么神仙D1T1，爆蛋T1，好像A了它或拿分的就几个人，，

---

The solution of T2:

题解是这么写的：和八皇后很像，八皇后是x+y和x-y来判重，这里就k1x+k2y来判重。

从各个点引出直线，带入原点检验方程即可。

注：

x/y = Δx/Δy

x*Δy = Δx*y

下面代码用了这个原理，省去了gcd（或除法）的时间复杂度或精度问题

Code：

#include <cstdio>
#include <map>
#include <algorithm>

using namespace std;

;
map <long long,int> M[N];
map <long long,int> T;
int n,m,i,j,k,q,tx,ty,s,num;
int x[N],y[N],dx[N],dy[N];
bool pd;

?a:gcd(b,a%b);}
int main()
{
    freopen("laser.in","r",stdin);
    freopen("laser.out","w",stdout);
    scanf("%d",&n);
    ;i<=n;i++)
    {
        scanf("%d%d",&tx,&ty);
        ) tx=-tx,ty=-ty;
        y[i]=-tx,x[i]=ty;
        tx=abs(y[i]),ty=abs(x[i]),k=gcd(tx,ty);
        y[i]=y[i]/k,x[i]=x[i]/k;
        ;j<i;j++)
            if ((x[i]==x[j]) && (y[i]==y[j]))
            {
                i--,n--;
                break;
            }
    }
    scanf("%d",&m);
    ;i<=m;i++)
    {
        scanf("%d%d",&tx,&ty);
        ;j<=n;j++)
            M[j][1LL*tx*x[j]+1LL*ty*y[j]]++;
        T[tx*()+ty]++;
    }
    scanf("%d",&q);
    ;i<=q;i++)
    {
        s=;
        scanf("%d%d",&tx,&ty);
        ;j<=n;j++)
            s=s+M[j][1LL*tx*x[j]+1LL*ty*y[j]];
        s=s-(n-)*T[tx*()+ty];
        printf("%d\n",s);
    }
    ;
}

T2

　　所以，我只拿了60分。神tmD1T2

---

　The solution of T3:

　　　　剪枝细节，，一堆的。不过和D1T3难度低一点吧。

　　　　考虑用 SPFA 迭代计算到达每个点存活且残余的最大 HP。（请注意加粗字体，旁边的大佬ldl因此 100->90 )

　　　　考虑到 SPFA 本 身是一个广搜的过程，自然也可以类似广搜地统计最少时间。因此，直接跑 SPFA 即可。时间复杂度 O(EAns)。

 

　　　　Code:

　　　　

#include <cstdio>
#include <algorithm>

using namespace std;

],next[],dist[],first[];
],d[],g[],h[],p[],r[];
int i,k,m,n,x,y,z,head,tail,sum_edge;

int main()
{
    freopen("game.in","r",stdin);
    freopen("game.out","w",stdout);
    scanf("%d%d%d",&n,&m,&k);
    ;i<=n;i++)
        scanf("%d",&r[i]);
    ;i<=m;i++)
    {
        scanf("%d%d%d",&x,&y,&z);
        sum_edge++,edge[sum_edge]=y,next[sum_edge]=first[x],dist[sum_edge]=z,first[x]=sum_edge;
        sum_edge++,edge[sum_edge]=x,next[sum_edge]=first[y],dist[sum_edge]=z,first[y]=sum_edge;
    }
    d[]=p[]=k;
    tail++,g[tail]=,h[tail]=;
    ;head<=tail;head++)
    {
        if (g[head]==n)
        {
            printf("%d\n",h[head]);
            ;
        }
        ])
            for (i=head;i<=tail;i++)
                d[g[i]]=p[g[i]],b[g[i]]=;
        ;i=next[i])
            if ((d[g[head]]>dist[i]) && (min(d[g[head]]-dist[i]+r[edge[i]],k)>p[edge[i]]))
            {
                p[edge[i]]=min(d[g[head]]-dist[i]+r[edge[i]],k);
                if (! b[edge[i]])
                    tail++,g[tail]=edge[i],h[tail]=h[head]+,b[edge[i]]=;
            }
    }
    printf("-1\n");
    ;
}

代码是老师的

　　　　

　　　　这题我莫名从60/70 -> 30？？？

　　　　

　　神tmT1T2