Java数据结构（十五）—— 多路查找树

多路查找树

二叉树和B树

二叉树的问题分析

• 二叉树操作效率高

• 二叉树需要加载到内存，若二叉树的节点多存在如下问题：

  1. 问题1：构建二叉树时，需多次进行I/O操作，对与速度有影响

  2. 问题2：节点海量造成二叉树的高度很大，会降低操作速度

多叉树

1. 在二叉树中，每个节点有数据项，最多有两个子节点。如果允许每个节点可以有更多的数据线和更多的子节点，就是多叉树（multiway tree)

2. 多叉树通过重新组织节点，减少树的高度，能对二叉树进行优化

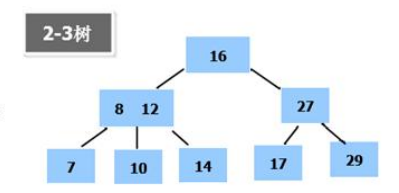
B树的基本介绍

B树通过重新组织节点，降低树的高度，并且减少I/O读写次数来提升效率

1. 如图B树通过重新组织节点降低了树的高度

2. 文件系统及数据库系统设计者利用了磁盘预读原理，将一个节点的大小设为等于一个页（页的大小为4k）这样每隔节点只需要一次I/O就可以完全载入

3. 将树的度M设置为1024，在600亿个元素中最多只需要4次I/O操作就可以读取到想要的元素，B树广泛应用于文件存储系统以及数据库系统中

节点度：节点子树的个数

树的度：节点度的最大值是树的度

2-3树

基本介绍

1. 2-3树是最简单的B-树结构

2. 2-3树的所有叶子节点都在同一层

3. 有两个子节点的节点叫二节点，二节点要么没有子节点，要么有两个子节点

4. 有三个子节点的节点叫三节点，三节点要么没有子节点，要么有三个子节点

5. 2-3树是由二节点和三节点构成的树

2-3树应用案例

要求

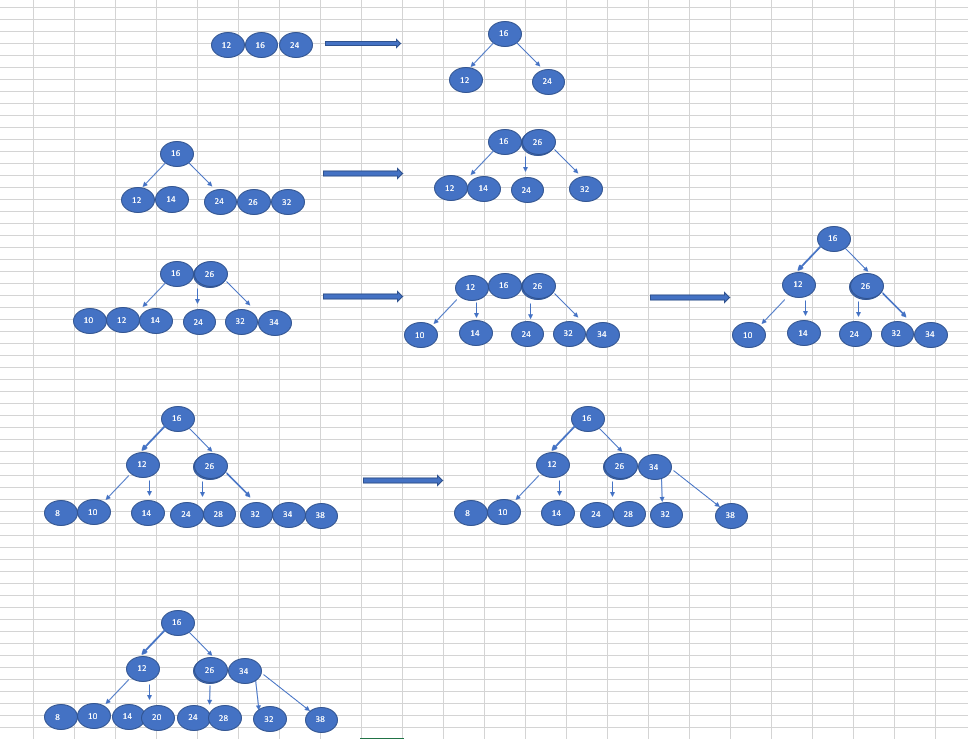
将数列{16，24，12，32，14，26，34，10，8，28，38，20}构建成2-3树，并保证数据插入的大小顺序。

插入规则

1. 2-3树的所有叶子节点都在同一层

2. 有两个子节点的节点叫二节点，二节点要么没有子节点，要么有两个子节点

3. 有三个子节点的节点叫三节点，三节点要么没有子节点，要么有三个子节点

4. 当按照规则插入一个数到某个节点时，不能满足上面的要求，就需要拆，先向上拆，如果上层满，则拆本层，拆后仍需满足上述条件

5. 对于三节点的子树的值大小仍然遵循（BST 二叉排序树）的规则

构建过程图解

B树、B+树和B*树

B树

• B-tree即B树，B即Balanced，平衡的意思。

• 2-3树和2-3-4树都是B树

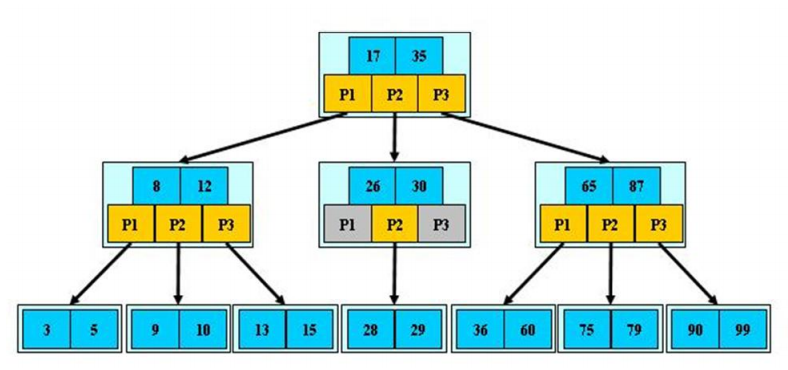
B树如图：

说明

1. B树的阶：节点的最多的子节点个数

2. B树的搜索，从根节点开始，对节点内的关键字（有序）序列进行二分查找，命中则退出，否则查找孩子节点，直到所对应的孩子指针为空，或已经是叶子节点

3. 关键字分布在整棵树中，即叶子节点和非叶子节点都存放数据

4. 搜索有可能在非叶子节点结束

5. 其搜索性等价于在关键字全集内做一次二分查找

B+树

• B+树是B树的变体，也是一种多路搜索树

如图：

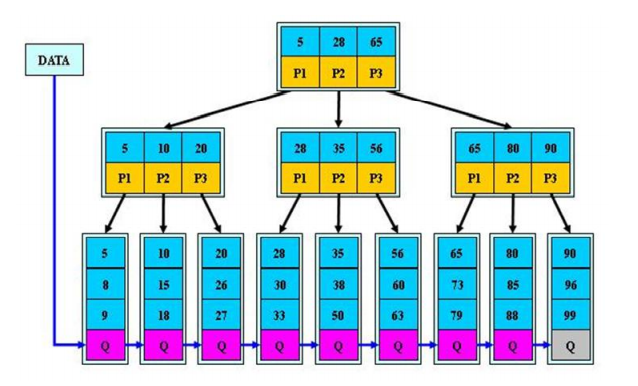
说明

1. B+树的搜索与B树基本相同，区别是B+树只有达到叶子节点才命中，其性能也等价于在关键字全集做一次二分查找

2. 所有关键字都出现在叶子节点的链表中，数据只能在叶子节点（稠密索引），且链表中的关键字是有序的

3. 非叶子节点相当于是叶子节点的所有（稀疏索引），叶子节点相当于是存储（关键字）数据的数据层

4. 更适合文件索引系统

5. B树和B+树各有自己的应用场景

B*树

• B*树是B+树的变体，在B+树的非根和非叶子节点再增加兄弟指针

如图

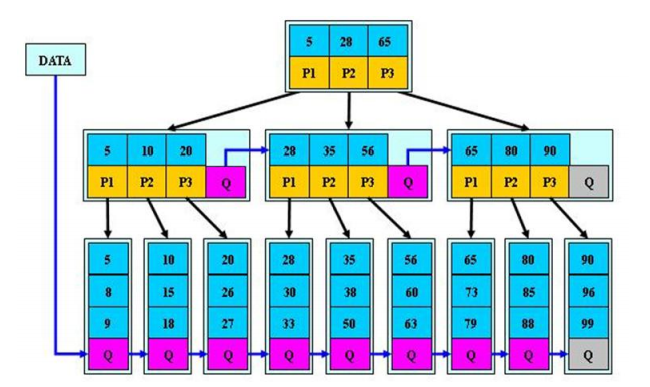
说明

1. B树定义了非叶子节点关键字个数至少为（2/3）M，即块的最低使用率为2/3，而B+树块的最低使用率为1/2

2. 从第一个特点可以看出，B*树分配新节点的概率比B+树要低，空间使用率更高

​

所有源码都可在gitee仓库中下载：https://gitee.com/vvwhyyy/java_algorithm