高斯混合模型GMM与EM算法的Python实现

GMM与EM算法的Python实现

高斯混合模型(GMM)是一种常用的聚类模型，通常我们利用最大期望算法(EM)对高斯混合模型中的参数进行估计。

---

1. 高斯混合模型(Gaussian Mixture models, GMM)

高斯混合模型（Gaussian Mixture Model，GMM）是一种软聚类模型。 GMM也可以看作是K-means的推广，因为GMM不仅是考虑到了数据分布的均值，也考虑到了协方差。和K-means一样，我们需要提前确定簇的个数。

GMM的基本假设为数据是由几个不同的高斯分布的随机变量组合而成。如下图，我们就是用三个二维高斯分布生成的数据集。

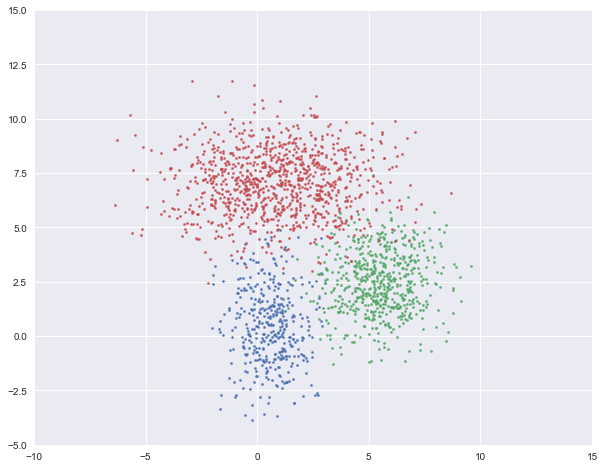
在高斯混合模型中，我们需要估计每一个高斯分布的均值与方差。从最大似然估计的角度来说，给定某个有n个样本的数据集X，假如已知GMM中一共有k 簇，我们就是要找到k组均值μ₁,⋯,μ_k，k组方差σ₁,⋯,σ_k 来最大化以下似然函数L

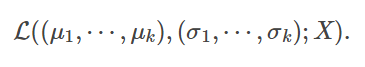
这里直接计算似然函数比较困难，于是我们引入隐变量(latent variable)，这里的隐变量就是每个样本属于每一簇的概率。假设W是一个n×k的矩阵，其中 W_i,j 是第 i 个样本属于第 j 簇的概率。

在已知W的情况下，我们就很容易计算似然函数L_W，

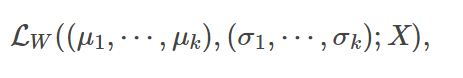
将其写成

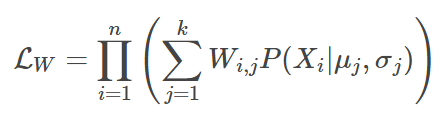
其中P(X_i | μ_j, σ_j) 是样本X_i在第j个高斯分布中的概率密度函数。

以一维高斯分布为例，

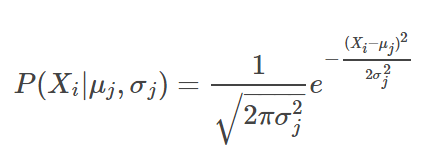
2. 最大期望算法(Expectation–Maximization, EM)

有了隐变量还不够，我们还需要一个算法来找到最佳的W，从而得到GMM的模型参数。EM算法就是这样一个算法。

简单说来，EM算法分两个步骤。

• 第一个步骤是E（期望），用来更新隐变量WW；
• 第二个步骤是M（最大化），用来更新GMM中各高斯分布的参量μ_j, σ_j。

然后重复进行以上两个步骤，直到达到迭代终止条件。

3. 具体步骤以及Python实现

完整代码在第4节。

首先，我们先引用一些我们需要用到的库和函数。

 import numpy as np
 import matplotlib.pyplot as plt
 from matplotlib.patches import Ellipse
 from scipy.stats import multivariate_normal
 plt.style.use('seaborn') 

接下来，我们生成2000条二维模拟数据，其中400个样本来自N(μ1,var1)，600个来自N(μ2,var2)，1000个样本来自N(μ3,var3)

 # 第一簇的数据
 num1, mu1, var1 = 400, [0.5, 0.5], [1, 3]
 X1 = np.random.multivariate_normal(mu1, np.diag(var1), num1)
 # 第二簇的数据
 num2, mu2, var2 = 600, [5.5, 2.5], [2, 2]
 X2 = np.random.multivariate_normal(mu2, np.diag(var2), num2)
 # 第三簇的数据
 num3, mu3, var3 = 1000, [1, 7], [6, 2]
 X3 = np.random.multivariate_normal(mu3, np.diag(var3), num3)
 # 合并在一起
 X = np.vstack((X1, X2, X3))

数据如下图所示：

 plt.figure(figsize=(10, 8))
 plt.axis([-10, 15, -5, 15])
 plt.scatter(X1[:, 0], X1[:, 1], s=5)
 plt.scatter(X2[:, 0], X2[:, 1], s=5)
 plt.scatter(X3[:, 0], X3[:, 1], s=5)
 plt.show()

3.1 变量初始化

首先要对GMM模型参数以及隐变量进行初始化。通常可以用一些固定的值或者随机值。

n_clusters 是GMM模型中聚类的个数，和K-Means一样我们需要提前确定。这里通过观察可以看出是3。（拓展阅读：如何确定GMM中聚类的个数？）

n_points 是样本点的个数。

Mu 是每个高斯分布的均值。

Var 是每个高斯分布的方差，为了过程简便，我们这里假设协方差矩阵都是对角阵。

W 是上面提到的隐变量，也就是每个样本属于每一簇的概率，在初始时，我们可以认为每个样本属于某一簇的概率都是1/3。

Pi 是每一簇的比重，可以根据W求得，在初始时，Pi = [1/3, 1/3, 1/3]

 n_clusters = 3
 n_points = len(X)
 Mu = [[0, -1], [6, 0], [0, 9]]
 Var = [[1, 1], [1, 1], [1, 1]]
 Pi = [1 / n_clusters] * 3
 W = np.ones((n_points, n_clusters)) / n_clusters
 Pi = W.sum(axis=0) / W.sum()

3.2 E步骤

E步骤中，我们的主要目的是更新W。第i个变量属于第m簇的概率为：

根据W，我们就可以更新每一簇的占比πm，

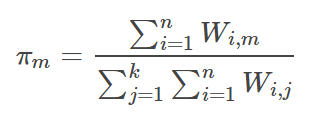
 def update_W(X, Mu, Var, Pi):
     n_points, n_clusters = len(X), len(Pi)
     pdfs = np.zeros(((n_points, n_clusters)))
     for i in range(n_clusters):
         pdfs[:, i] = Pi[i] * multivariate_normal.pdf(X, Mu[i], np.diag(Var[i]))
     W = pdfs / pdfs.sum(axis=1).reshape(-1, 1)
     return W

 def update_Pi(W):
     Pi = W.sum(axis=0) / W.sum()
     return Pi

以下是计算对数似然函数的logLH以及用来可视化数据的plot_clusters。

 def logLH(X, Pi, Mu, Var):
     n_points, n_clusters = len(X), len(Pi)
     pdfs = np.zeros(((n_points, n_clusters)))
     for i in range(n_clusters):
         pdfs[:, i] = Pi[i] * multivariate_normal.pdf(X, Mu[i], np.diag(Var[i]))
     return np.mean(np.log(pdfs.sum(axis=1)))

 def plot_clusters(X, Mu, Var, Mu_true=None, Var_true=None):
     colors = ['b', 'g', 'r']
     n_clusters = len(Mu)
     plt.figure(figsize=(10, 8))
     plt.axis([-10, 15, -5, 15])
     plt.scatter(X[:, 0], X[:, 1], s=5)
     ax = plt.gca()
     for i in range(n_clusters):
         plot_args = {'fc': 'None', 'lw': 2, 'edgecolor': colors[i], 'ls': ':'}
         ellipse = Ellipse(Mu[i], 3 * Var[i][0], 3 * Var[i][1], **plot_args)
         ax.add_patch(ellipse)
     if (Mu_true is not None) & (Var_true is not None):
         for i in range(n_clusters):
             plot_args = {'fc': 'None', 'lw': 2, 'edgecolor': colors[i], 'alpha': 0.5}
             ellipse = Ellipse(Mu_true[i], 3 * Var_true[i][0], 3 * Var_true[i][1], **plot_args)
             ax.add_patch(ellipse)
     plt.show()

3.2 M步骤

M步骤中，我们需要根据上面一步得到的W来更新均值Mu和方差Var。 Mu和Var是以W的权重的样本X的均值和方差。

因为这里的数据是二维的，第m簇的第k个分量的均值，

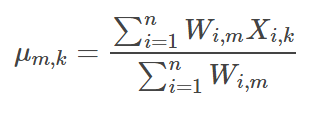
第m簇的第k个分量的方差，

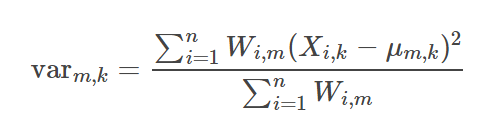
以上迭代公式写成如下函数update_Mu和update_Var。

 def update_Mu(X, W):
     n_clusters = W.shape[1]
     Mu = np.zeros((n_clusters, 2))
     for i in range(n_clusters):
         Mu[i] = np.average(X, axis=0, weights=W[:, i])
     return Mu

 def update_Var(X, Mu, W):
     n_clusters = W.shape[1]
     Var = np.zeros((n_clusters, 2))
     for i in range(n_clusters):
         Var[i] = np.average((X - Mu[i]) ** 2, axis=0, weights=W[:, i])
     return Var

3.3 迭代求解

下面我们进行迭代求解。

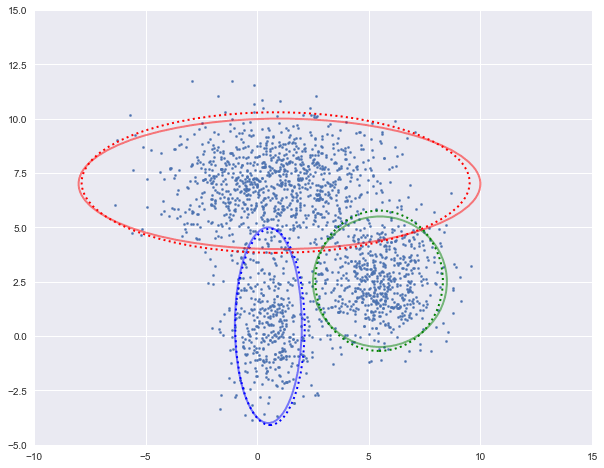
图中实现是真实的高斯分布，虚线是我们估计出的高斯分布。可以看出，经过5次迭代之后，两者几乎完全重合。

 loglh = []
 for i in range(5):
     plot_clusters(X, Mu, Var, [mu1, mu2, mu3], [var1, var2, var3])
     loglh.append(logLH(X, Pi, Mu, Var))
     W = update_W(X, Mu, Var, Pi)
     Pi = update_Pi(W)
     Mu = update_Mu(X, W)
     print('log-likehood:%.3f'%loglh[-1])
     Var = update_Var(X, Mu, W)

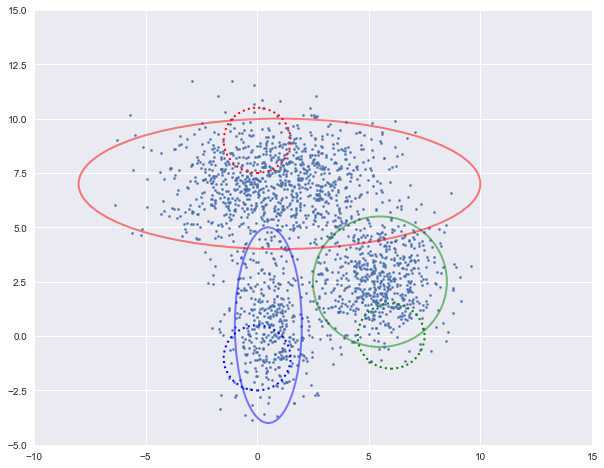
 log-likehood:-8.054

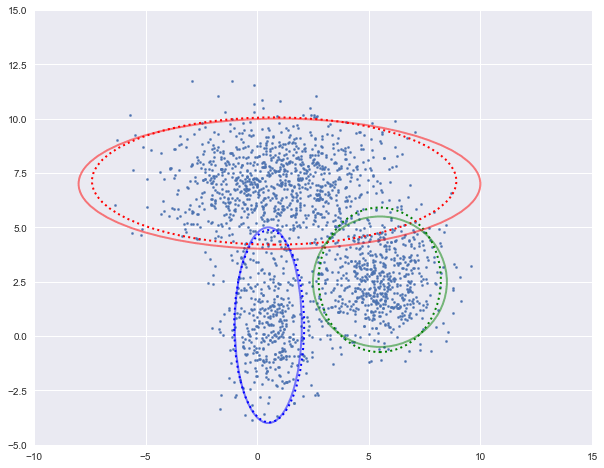
 log-likehood:-4.731

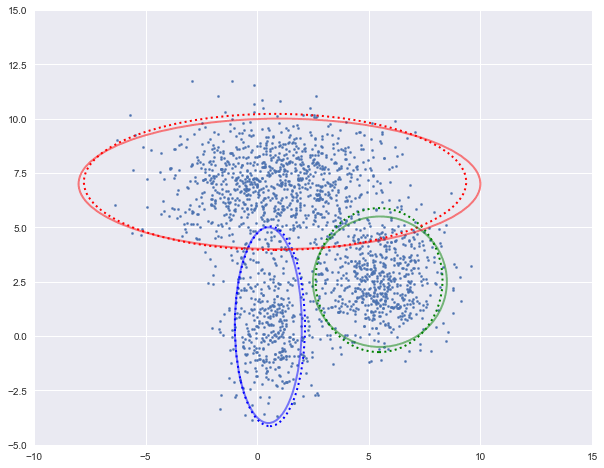
 log-likehood:-4.729

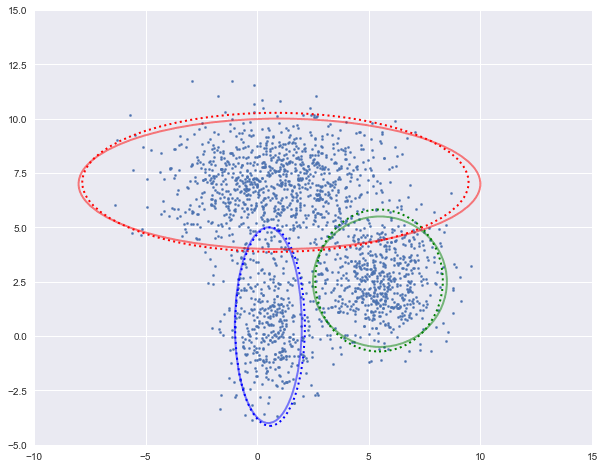
 log-likehood:-4.728

 log-likehood:-4.728

4. 完整代码

 import numpy as np
 import matplotlib.pyplot as plt
 from matplotlib.patches import Ellipse
 from scipy.stats import multivariate_normal
 plt.style.use('seaborn')

 # 生成数据
 def generate_X(true_Mu, true_Var):
     # 第一簇的数据
     num1, mu1, var1 = 400, true_Mu[0], true_Var[0]
     X1 = np.random.multivariate_normal(mu1, np.diag(var1), num1)
     # 第二簇的数据
     num2, mu2, var2 = 600, true_Mu[1], true_Var[1]
     X2 = np.random.multivariate_normal(mu2, np.diag(var2), num2)
     # 第三簇的数据
     num3, mu3, var3 = 1000, true_Mu[2], true_Var[2]
     X3 = np.random.multivariate_normal(mu3, np.diag(var3), num3)
     # 合并在一起
     X = np.vstack((X1, X2, X3))
     # 显示数据
     plt.figure(figsize=(10, 8))
     plt.axis([-10, 15, -5, 15])
     plt.scatter(X1[:, 0], X1[:, 1], s=5)
     plt.scatter(X2[:, 0], X2[:, 1], s=5)
     plt.scatter(X3[:, 0], X3[:, 1], s=5)
     plt.show()
     return X

 # 更新W
 def update_W(X, Mu, Var, Pi):
     n_points, n_clusters = len(X), len(Pi)
     pdfs = np.zeros(((n_points, n_clusters)))
     for i in range(n_clusters):
         pdfs[:, i] = Pi[i] * multivariate_normal.pdf(X, Mu[i], np.diag(Var[i]))
     W = pdfs / pdfs.sum(axis=1).reshape(-1, 1)
     return W

 # 更新pi
 def update_Pi(W):
     Pi = W.sum(axis=0) / W.sum()
     return Pi

 # 计算log似然函数
 def logLH(X, Pi, Mu, Var):
     n_points, n_clusters = len(X), len(Pi)
     pdfs = np.zeros(((n_points, n_clusters)))
     for i in range(n_clusters):
         pdfs[:, i] = Pi[i] * multivariate_normal.pdf(X, Mu[i], np.diag(Var[i]))
     return np.mean(np.log(pdfs.sum(axis=1)))

 # 画出聚类图像
 def plot_clusters(X, Mu, Var, Mu_true=None, Var_true=None):
     colors = ['b','g','r']
     n_clusters = len(Mu)
     plt.figure(figsize=(10,8))
     plt.axis([-10,15,-5,15])
     plt.scatter(X[:,0], X[:,1], s=5)
     ax = plt.gca()for i in range(n_clusters):
         plot_args ={'fc':'None','lw':2,'edgecolor': colors[i],'ls':':'}
         ellipse =Ellipse(Mu[i],3*Var[i][0],3*Var[i][1],**plot_args)
         ax.add_patch(ellipse)if(Mu_trueisnotNone)&(Var_trueisnotNone):for i in range(n_clusters):
             plot_args ={'fc':'None','lw':2,'edgecolor': colors[i],'alpha':0.5}
             ellipse =Ellipse(Mu_true[i],3*Var_true[i][0],3*Var_true[i][1],**plot_args)
             ax.add_patch(ellipse)
     plt.show()# 更新Mudef update_Mu(X, W):
     n_clusters = W.shape[1]Mu= np.zeros((n_clusters,2))for i in range(n_clusters):Mu[i]= np.average(X, axis=0, weights=W[:, i])returnMu# 更新Vardef update_Var(X,Mu, W):
     n_clusters = W.shape[1]Var= np.zeros((n_clusters,2))for i in range(n_clusters):Var[i]= np.average((X -Mu[i])**2, axis=0, weights=W[:, i])returnVarif __name__ =='__main__':# 生成数据
     true_Mu =[[0.5,0.5],[5.5,2.5],[1,7]]
     true_Var =[[1,3],[2,2],[6,2]]
     X = generate_X(true_Mu, true_Var)# 初始化
     n_clusters =3
     n_points = len(X)Mu=[[0,-1],[6,0],[0,9]]Var=[[1,1],[1,1],[1,1]]Pi=[1/ n_clusters]*3
     W = np.ones((n_points, n_clusters))/ n_clusters
     Pi= W.sum(axis=0)/ W.sum()# 迭代
     loglh =[]for i in range(5):
         plot_clusters(X,Mu,Var, true_Mu, true_Var)
         loglh.append(logLH(X,Pi,Mu,Var))
         W = update_W(X,Mu,Var,Pi)Pi= update_Pi(W)Mu= update_Mu(X, W)print('log-likehood:%.3f'%loglh[-1])Var= update_Var(X,Mu, W)

本教程基于Python 3.6。

原创者：u_u | 修改校对：SofaSofa TeamM | 转自： http://sofasofa.io/tutorials/gmm_em/