CF264D - Colorful Stones 题解

题面

官方题解

模拟赛题解

题解概述：





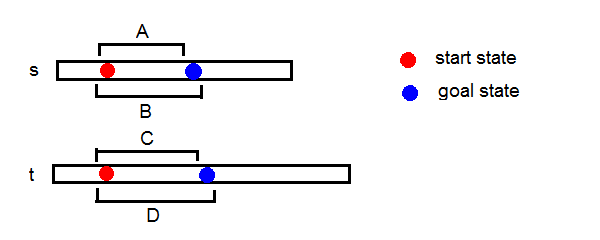
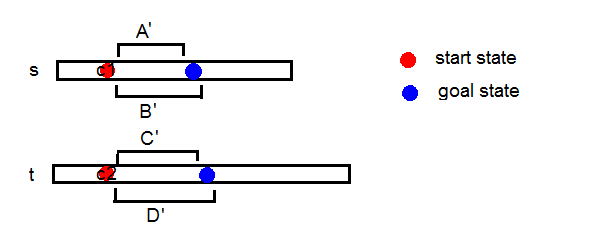
定义符号A_{B表示序列A是序列B的子序列，A!}B反之。

设操作序列为I,则有A_I,B!I,C_I,D!I。

可得出条件①B!_C且D!A，所以我们只要讨论满足这个条件的情况。

分情况讨论：

1. c1=c2，则可以进行操作c1，得到的状态仍满足条件①；
2. c1!=c2，且B'!~C，此时可以进行操作c1；
3. c1!=c2，且D'!~A，此时可以进行操作c2；
4. c1!=c2，且D'_A,B'C，此时无法进行操作，此情况无解；
   
   我们还发现第4种情况下，B=...xyxy，D=...yxyx，且B,D长度相等。
   
   另外，当B以xy结尾，D以yx结尾时，此情况一定无解。

这就证明了当满足条件①时，无解当且仅当B以xy结尾，D以yx结尾。

这样就可以对于数对(x,y)的每一个x，求出对应y的范围（一段区间），然后把其中以yx结尾的y减去（用前缀和实现），就可以得到每一个x的答案了。

总复杂度O(n)。

代码：

#include<bits/stdc++.h>
using namespace std;
#define N 2000007
#define ll long long
int a[N],b[N],s[3][3][N];
char ch[N];
int tar(char c)
{
	if(c=='R')return 0;
	if(c=='B')return 1;
	return 2;
}
int main()
{
	//freopen("stone.in","r",stdin);
	//freopen("stone.out","w",stdout);
	int n,m,i,j,l,r;
	ll ans=0;
	scanf("%s",ch+1);
	n=strlen(ch+1);
	for(i=1;i<=n;i++)
		a[i]=tar(ch[i]);
	scanf("%s",ch+1);
	m=strlen(ch+1);
	for(i=1;i<=m;i++)
		b[i]=tar(ch[i]);
	for(int x=0;x<=2;x++)
		for(int y=0;y<=2;y++)
		{
			for(i=2;i<=m;i++)
				if(b[i-1]==x&&b[i]==y)
					s[x][y][i]=1;
			for(i=1;i<=m;i++)
				s[x][y][i]+=s[x][y][i-1];
		}
	l=1,r=1;
	while(r<m&&b[r]!=a[1])r++;
	ans=r-l+1;
	for(i=2;i<=n;i++)
	{
		if(l<=m&&a[i-1]==b[l])l++;
		if(l>m)break;
		if(r<m)
		{
			r++;
			while(r<m&&b[r]!=a[i])r++;
		}
		if(l>r)continue;
		int x=a[i-1],y=a[i];
		ans+=r-l+1;
		if(x!=y)ans-=s[y][x][r]-s[y][x][l-1];
	}
	printf("%lld\n",ans);
	return 0;
}

总结：这个问题通过设出操作序列I，通过子序列的模型来描述题目条件，然后排除一些显然不合法的情况，确立一个有解的基本条件，再在这个条件下递归地讨论一种情况合不合法，最终发现无解的情况比较特殊，于是得到了一个易于判断的无解的充要条件，问题解决。