图的遍历（搜索）算法（深度优先算法DFS和广度优先算法BFS）

图的遍历的定义：

从图的某个顶点出发访问遍图中所有顶点，且每个顶点仅被访问一次。（连通图与非连通图）

深度优先遍历（DFS）；

1、访问指定的起始顶点；

2、若当前访问的顶点的邻接顶点有未被访问的，则任选一个访问之；反之，退回到最近访问过的顶点；直到与起始顶点相通的全部顶点都访问完毕；

3、若此时图中尚有顶点未被访问，则再选其中一个顶点作为起始顶点并访问之，转 2； 反之，遍历结束。

连通图的深度优先遍历类似于树的先根遍历

如何判别V的邻接点是否被访问？

解决办法：为每个顶点设立一个“访问标志”。首先将图中每个顶点的访问标志设为 FALSE,  之后搜索图中每个顶点，如果未被访问，则以该顶点为起始点，进行深度

优先遍历，否则继续检查下一顶点。

 

访问指定的起始顶点；若当前访问的顶点的邻接顶点有未被访问的，则任选一个访问之；

反之，退回到最近访问过的顶点；直到与起始顶点相通的全部顶点都访问完毕；

 

回退到1，发现了新的没有被访问的结点

继续回退，回退到0

再也找不到新的结点了，那么回退，回退到起始顶点，结束搜索

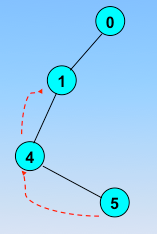
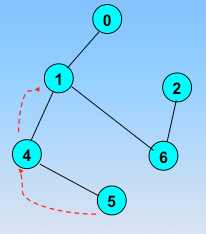
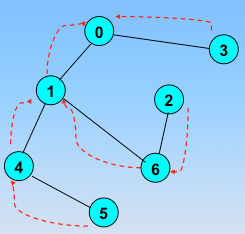
顶点的访问序列为：    v0 , v1 , v4 , v5 , v6 , v2 , v3（不唯一）

实现过程：依靠栈，一维数组和图的邻接矩阵存储方式

图的邻接矩阵存储方式

 

使用一个一维数组存储所有的顶点，对应的下标的元素为1（代表已经被访问），0（代表没有被访问）

 

先访问 v1，0进栈，0处置为1

 

继续访问 v2，1进栈，1处置为1

 

继续访问v4（依据邻接矩阵），3入栈，3处置为1

 

继续访问 v8，7入栈，7处置为1

 

继续访问 v5，4入栈，4处置为1

 

继续访问，发现没有还没访问的结点了，那么好，退栈（也就是回退）开始，回退到 v1处，也就是0的时候，发现了没有被访问的结点，那么继续访问之

继续访问 v3，2进栈，2处置为1，继续访问v6，5进栈，5处置为1，继续访问v7，6进栈，6处置为1

 

发现没有还没被访问的结点了，那么好，继续回退（也就是退栈的过程）

 

 

一直到栈空，说明深度优先搜索完毕。结束程序。

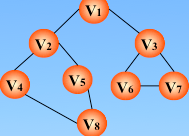
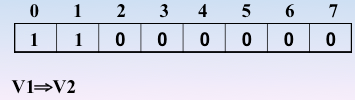
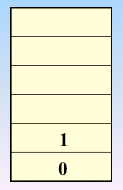
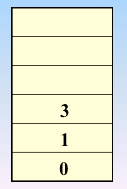
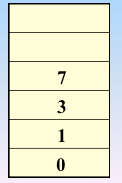
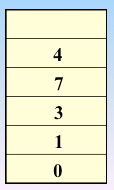
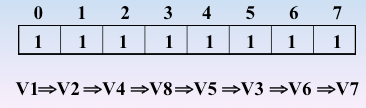
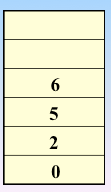
遍历图的过程实质上是对每个顶点查找其邻接点的过程，所耗费的时间取决于所采用的存储结构。
对图中的每个顶点至多调用1次DFS算法，因为一旦某个顶点已访问过，则不再从它出发进行搜索。

邻接链表表示：查找每个顶点的邻接点所需时间为O(e)，e为边(弧)数，算法时间复杂度为O(n+e)

数组表示：查找每个顶点的邻接点所需时间为O(n2)，n为顶点数，算法时间复杂度为O(n2)

代码如下

//访问标志数组
int visited[MAX] = {};

//用邻接表方式实现深度优先搜索(递归方式）
//v 传入的是第一个需要访问的顶点
void DFS(MGraph G, int v)
{
    //图的顶点的搜索指针
    ArcNode *p;
    //置已访问标记
    visited[v] = ;
    //输出被访问顶点的编号
    printf("%d  ", v);
    //p指向顶点v的第一条弧的弧头结点
    p = G.vertices[v].firstarc;
    while (p != NULL)
    {
        //若p->adjvex顶点未访问,递归访问它
        if (visited[p->adjvex] == )
        {
            DFS(G, p->adjvex);
        }
        //p指向顶点v的下一条弧的弧头结点
        p = p->nextarc;
    }
}

广度优先搜索（BFS）

方法：从图的某一结点出发，首先依次访问该结点的所有邻接顶点 Vi1, Vi2, …, Vin 再按这些顶点被访问的先后次序依次访问与它们相邻接的所有未被访问的顶点，重复此过程，直至所有顶点均被访问为止。

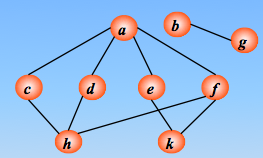
顶点的访问次序

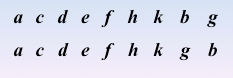
实现过程：依靠队列和一维数组来实现

 #include <iostream>
 #include<queue>
 using namespace std;

 const int MAX = ;
 //辅助队列的初始化，置空的辅助队列Q，类似二叉树的层序遍历过程
 queue<int> q;
 //访问标记数组
 bool visited[MAX];
 //图的广度优先搜索算法
 void BFSTraverse(Graph G, void (*visit)(int v))
 {
     int v = ;
     //初始化访问标记的数组
     for (v = ; v < G.vexnum; v++)
     {
         visited[v] = false;
     }
     //依次遍历整个图的结点
     for (v = ; v < G.vexnum; v++)
     {
         //如果v尚未访问，则访问 v
         if  (!visited[v])
         {
             //把 v 顶点对应的数组下标处的元素置为真，代表已经访问了
             visited[v] = true;
             //然后v入队列，利用了队列的先进先出的性质
             q.push(v);
             //访问 v，打印处理
             cout << q.back() << " ";
             //队不为空时
             while (!q.empty())
             {
                 //队头元素出队,并把这个出队的元素置为 u，类似层序遍历
                 Graph *u = q.front();
                 q.pop();
                 //w为u的邻接顶点
                 for (int w = FirstAdjVex(G, u); w >= ; w = NextAdjVex(G,u,w))
                 {
                     //w为u的尚未访问的邻接顶点
                     if (!visited[w])
                     {
                         visited[w] = true;
                         //然后 w 入队列，利用了队列的先进先出的性质
                         q.push(w);
                         //访问 w，打印处理
                         cout << q.back() << " ";
                     }//end of if
                 }//end of for
             }//end of while
         }//end of if
     }// end of for
 }

欢迎关注

dashuai的博客是终身学习践行者，大厂程序员，且专注于工作经验、学习笔记的分享和日常吐槽，包括但不限于互联网行业，附带分享一些PDF电子书，资料，帮忙内推，欢迎拍砖！