Manacher 学习笔记

$\\$

$Manacher$

一种常用的字符串算法，用于处理一些回文字符相关的问题。

回文串：从前向后和从后向前输出一致。
回文中心：以这里开始，每次向外左右各扩展一个字符得到的回文串的中心。
回文半径：定义在字符串的一个字符或两个字符的间隙上，代表以这里为回文中心的最长回文串的半径，具体的说，如果位置$i$延申出的最长回文串区间为$[l,r]$，那么他的回文半径就是$r-i+1$。

$Manacher$最基本的操作，就是求出以一个字符串的每一个字符和间隙为回文中心，对应的回文半径。

$\\$

具体操作

$\\$

首先考虑间隙这个问题。由于便于描述间隙的回文半径，$Manacher$使用了一种巧妙的转化：

在每一个间隙（包括第一个字符前和最后一个字符后）各插上一个特殊字符，即原字符串中没有出现过的字符。为了不影响原串的正反匹配，所加的字符都是一样的。为了避免头尾匹配越界，头尾各放置一个与上述提到过的所有字符均不同的字符，且这两个字符也要不同。

我的方式一般是正常插入#，两侧分别插入不同的中括号。形象化的表示：

注意两侧多添加的字符只是为了匹配不越界，并不用于统计回文半径。

$\\$

关于还原回原串的回文长度问题我们后面再讲，先考虑最优秀的复杂度求出新串所有位置的回文半径是多少。

线性。设$len_i$表示新字符串中以$i$为回文中心的回文半径，做的时候维护两个变量$Maxr$和$Maxp$，第一个代表当前已经处理过的回文中心，其创造的回文子串最远延申到的字符位置，第二个就是对应的回文中心。

然后考虑如何快速的得到当前要求的位置$i$的答案，若$i\not=1$，显然有$i>Maxp$。

我们可以用对称性很快的找到$i$关于$Maxp$的对称点$i'$，并且之前已经确定了$len_{i'}$。观察下面的两种情况。

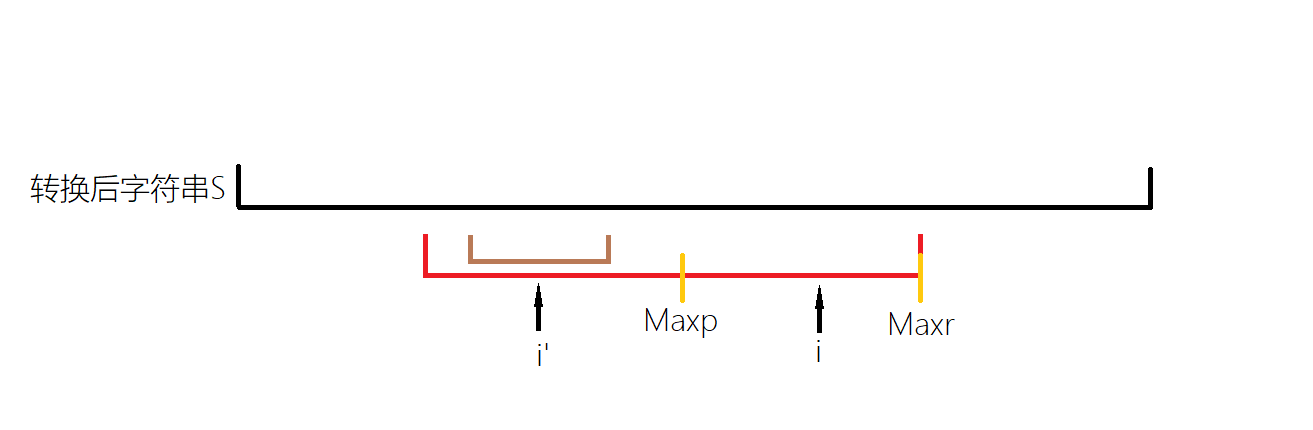
线段都表示以对应点为回文中心的最长回文子串。这一情况中，对称点的子串范围再对称回来并没有超过$Maxp$的子串范围，因为红色的大串是回文的，所以两侧的情况应该相同，即$i$所对应的回文子串长度应该与$i'$相同，$len_i=len_{i'}$。

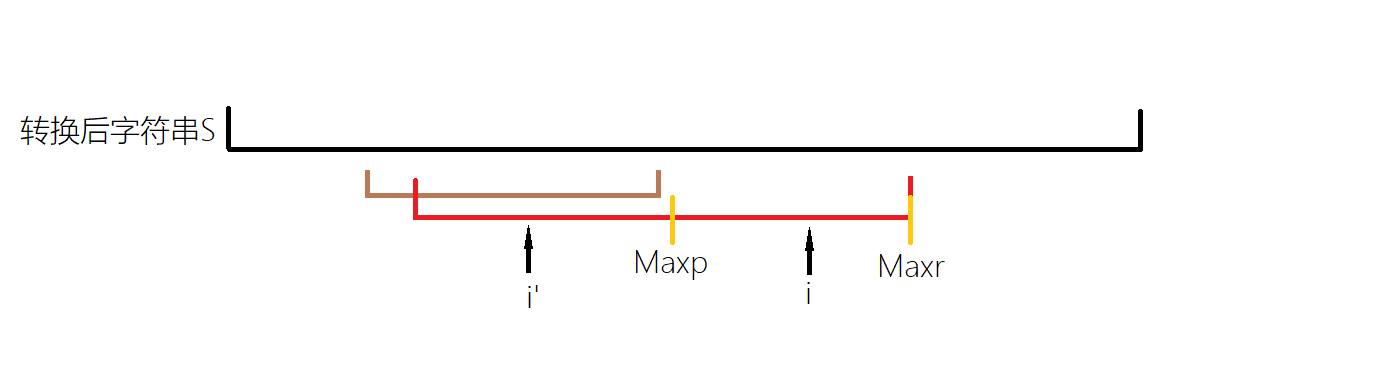
这一情况中，我们一定能保证，以红色左端点为起点，以$i'$为对称中心的对称点为终点的部分，再关于$Maxp$对称过去是$i$可延伸的一个回文子串，但是再长因为超过了当前$Maxr$的范围，所以不能确定。这一情况下，先令$len_i=len_{i'}$，再一个一个位置的尝试向外扩展。

当前位置直接超过$Maxr$时，我们也视作第二种情况。

当前位置的右端点超过$Maxr$时，更新$Maxr$和$Maxp$。

for(R int i=1,p=0,mr=0;i<=n;++i){

    len[i]=i>mr?1:min(mr-i+1,len[(p<<1)-i]);

    while(s[i-len[i]]==s[i+len[i]]) ++len[i];

    if(i+len[i]-1>mr){p=i;mr=i+len[i]-1;}

}

预处理部分就不放代码了，核心其实就这四行。

$\\$

复杂度证明和一些推论

$\\$

粗略的复杂度证明。扫描是$\text O(N)$的，每一个第一种情况得到答案是$\text O(1)$的，第二种情况至多只会出现$N$次，且每一次需要扩展右端点的扫描距离之和等于$N$，这种类似于双指针扫描的东西复杂度是线性的。

$\\$

有一个特殊的性质，即一个字符在原字符串的意义下$($#号即代表一个间隙$)$做回文中心，他延申出的最长回文子串的长度，等于转化之后的字符串中，他的回文半径$-1$。我们分两种情况讨论证明它。

转化后的字符为特殊字符$($#号$)$。这一情况中得到的回文串，从这个#号开始的部分一定是形如#a#b....#z#的，注意到在不算中间字符时，右一半的#号和原串字符个数是一样的，左一半也是一样。因为中间字符不是原串字符，所以$len-1$就是以这个#号为回文中心，延伸出的最长回文子串的长度。
原串的字符。这一情况得到的回文串，从这个字符开始的部分一定是形如a#b#.....z#的形式，这一情况下不算中间字符时，右一半#号个数比原串字符个数多一，左一半也是这样，所以右一侧回文半径中所有的#号都拿左侧的换，还多一个#号，正好用回文中心换掉。

关于上面的“一定是形如”部分，粗略的说明可以理解成，每个字符一定是被两个#号围着的，没有任何一个原串字符两侧出现除掉#号以外的其他字符。

$\\$

还有一个定理可以得出，是一个字符串最多只有$N$个本质不同的回文子串。

考虑终点相同的回文子串，可以发现短的回文子串在大的回文子串中，因此对称过去在前面出现过。所以以某一个位置为终点且第一次出现的回文子串最多只有一个。这也是$Manacher$时间复杂度有保证的原因，因为如果$Maxr$不更新，就不会出现本质不同的回文子串，前面已经出现过了。而每扩展一次$Maxr$，最多新出现一个本质不同的回文子串。

$\\$

一道例题

$\\$

给出一个长度为$N$字符串，每个回文的部分都是一个碎片（碎片之间可部分重合），求最少多少次拼合碎片能够得出原字符串，拼合的定义是只要不完全相同就可以连接在一起，如果头尾有相同的部分可以重合。如$aba$和$aca$连接起来，可以生成串$abaaca$或 $abaca$。

$N\in [5\times10^4]$，多组数据。

$\\$

$Manacher$板子。求出所有回文串在原字符串中的覆盖区间，就是最少线段完全覆盖问题，贪心即可。

关于为什么一定是最长回文子串的问题，考虑两个回文串想要重叠的部分，划给哪一侧另一侧都会失去那么长的长度，所以最长的回文子串可以代表所有子串的最优答案。

有一个化简是，注意到能覆盖一个字符，就一定能覆盖两侧的#号，所以直接统计在变化后的串每一个回文串的覆盖区间即可，不用还原回去。需要注意拼合的次数是总段数$-1$。

$\\$

#include<cmath>

#include<cstdio>

#include<cctype>

#include<string>

#include<cstdlib>

#include<cstring>

#include<iostream>

#include<algorithm>

#define N 50010

#define R register

using namespace std;

char s[N<<1],sr[N];

int p,mr,now,ans,slen,len[N<<1];

struct line{int l,r;}seg[N<<1];

inline bool cmp(line x,line y){return x.l<y.l;}

inline void init(){

  p=mr=ans=0;

  s[now=1]='#';

  slen=strlen(sr);

  for(R int i=0;i<slen;++i){s[++now]=sr[i];s[++now]='#';}

  s[0]='['; s[now+1]=']';

}

inline void manacher(){

  for(R int i=1;i<=now;++i){

    len[i]=(i>mr)?1:min(mr-i+1,len[(p<<1)-i]);

    while(s[i-len[i]]==s[i+len[i]]) ++len[i];

    if(i+len[i]-1>mr){mr=i+len[i]-1;p=i;}

    seg[i].l=i-len[i]+1; seg[i].r=i+len[i]-1;

  }

}

inline void calc(){

  sort(seg+1,seg+1+now,cmp);

  for(R int i=1,nowr=1,tmp=0;i<=now;){

    while(seg[i].l<=nowr&&i<=now) tmp=max(tmp,seg[i].r),++i;

    if(tmp+1<=nowr) break;

    ++ans; nowr=tmp+1;

  }

  printf("%d\n",ans-1);

}

int main(){

  while(scanf("%s",sr)!=EOF){init();manacher();calc();}

  return 0;

}