二叉堆练习3&【模板】堆

时间限制: 3 s 空间限制: 128000 KB 题目等级 : 黄金 Gold

题目描述 Description

给定N(N≤500,000)和N个整数(较有序)，将其排序后输出。

输入描述 Input Description

N和N个整数

输出描述 Output Description

N个整数(升序)

样例输入 Sample Input

5

12 11 10 8 9

样例输出 Sample Output

8 9 10 11 12

数据范围及提示 Data Size & Hint

对于33%的数据 N≤10000

对于另外33%的数据 N≤100,000  0≤每个数≤1000

对于100%的数据 N≤500,000  0≤每个数≤2*10^9

代碼實現：

 #include<iostream>
 #include<cstdio>
 using namespace std;
 int n,a,b,c,dp,ado,rec;
 int heap[];//數組要開的大一些。
 void put(int x){
     ++dp;
     heap[dp]=x;
     rec=dp;
     while(rec>){
         if(heap[rec]<heap[rec/]){
             swap(heap[rec],heap[rec/]);
             rec/=;
         }
         else break;
     }
 }
 int get(){
     int d=,e;
     rec=heap[d];
     heap[d]=heap[dp];
     dp--;
     while(d*<=dp){
         if(heap[d*]>heap[d*+]) c=d*+;
         else c=d*;
         if(heap[d]>heap[c]){
             swap(heap[d],heap[c]);
             d=c;
         }
         else break;
     }
     return rec;
 }
 int main(){
     cin>>n;
     for(int i=;i<=n;i++){
         cin>>a;
         put(a);
     }
     for(int i=;i<=n;i++) printf("%d ",get());
     return ;
 }

一個堆排的裸題。

题目来源：CODE[VS]

题目描述

如题，初始小根堆为空，我们需要支持以下3种操作：

操作1： 1 x 表示将x插入到堆中

操作2： 2 输出该小根堆内的最小数

操作3： 3 删除该小根堆内的最小数

输入输出格式

输入格式：

第一行包含一个整数N，表示操作的个数

接下来N行，每行包含1个或2个正整数，表示三种操作，格式如下：

操作1： 1 x

操作2： 2

操作3： 3

输出格式：

包含若干行正整数，每行依次对应一个操作2的结果。

输入输出样例

输入样例#1：

5
1 2
1 5
2
3
2

输出样例#1：

2
5

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=15

对于70%的数据：N<=10000

对于100%的数据：N<=1000000（注意是6个0。。。不过不要害怕，经过编者实测，堆是可以AC的）

样例说明：

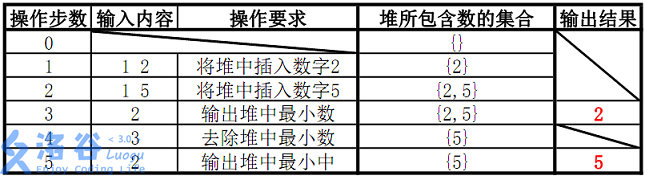
故输出为2、5

代码实现：

 #include<cstdio>
 #include<iostream>
 using namespace std;
 int n,a,b,c;
 int heap[],k;
 void mai(int x){
     int lson=x*,rson=x*+;
     if(lson>k) return;
     if(heap[lson]<heap[rson]||rson>k){
         if(heap[x]>heap[lson]){
             swap(heap[x],heap[lson]);
             mai(lson);
         }
     }
     else{
         if(heap[x]>heap[rson]){
             swap(heap[x],heap[rson]);
             mai(rson);
         }
     }
 }
 void put(int x){
     heap[++k]=x;
     c=k;
     while(heap[c]<heap[c/]&&c/){
         swap(heap[c],heap[c/]);
         c/=;
     }
 }
 void push(){
     heap[]=heap[k--];
     mai();
 }
 int main(){
     scanf("%d",&n);
     for(int i=;i<=n;i++){
         scanf("%d",&a);
         if(a==){
             scanf("%d",&b);
             put(b);
         }
         if(a==) printf("%d\n",heap[]);
         if(a==) push();
     }
     return ;
 }

这份代码比上面的快。

题目来源：洛谷