数据结构哈夫曼树（C语言版）
文章目录
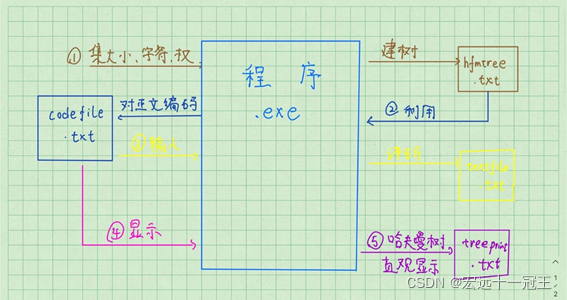
一、 问题
需求分析
此图转载于账号u014447560（深海鲸歌）
代码分析
结构体定义使用
需要定义树的结构，打印树的结构时需要用的队列
typedef struct node{
char data;
int weight;
int parent;
int lchild,rchild;
int mark;
}huffmanTree;
typedef struct code_N{
char ch;
char Bi_code[100];
}Char_coding;
typedef struct queue_node{
int data;
struct LinkNode *next;
}LinkNode;
typedef struct queue{
struct queue_node* rear,*front;
}LinkQueue;
int allchar =0; //记录所有字母的个数
建立哈夫曼树，首先需要找到两个权值最小的两个叶子结点,然后建树
初始化树
void find_min(huffmanTree *tree,int max,int *firstMin,int *secMin){
//查找两个最小的值
int smallindex[2];
for(int j = 0;j<2;j++){
int temp = 9999;
int count = 0;
int final_index =0;
for(int k = 0;k<=max;k++) {
if(tree[k].mark==0){
if(tree[k].weight<temp){
final_index = k;
temp = tree[k].weight;
}
}
else{
count++;
}
// 最后一个结点
if(count ==max &&j ==0){
return ;
}
}
tree[final_index].mark =1;
smallindex[j] = final_index;
}
*firstMin = smallindex[0];
*secMin =smallindex[1];
}
//建树
huffmanTree * Init_huffmanTree(huffmanTree *tree,char *ch,int *weight){
int all_node;
int count = strlen(ch);
if(strlen(ch)<0){
return NULL;
}
all_node = 2*count -1;
// 初始化哈夫曼树
tree = (huffmanTree*) malloc((all_node)*sizeof (huffmanTree));
for(int i = 0;i<count;i++){
tree[i].data =ch[i];
tree[i].weight = weight[i];
tree[i].parent =-1;
tree[i].lchild=-1;
tree[i].rchild =-1;
tree[i].mark =0;
}
for(int j = count;j<all_node;j++){
tree[j].data ='#';
tree[j].parent =-1;
tree[j].weight =-1;
tree[j].parent =tree[j].rchild=tree[j].lchild =-1;
tree[j].mark =0;
}
for(int i = count;i<all_node;i++){
int fristMin,secMin;
fristMin = secMin = 0;
find_min(tree,i-1,&fristMin,&secMin); //找到最小索引的两个的下标
tree[fristMin].parent = i;
tree[secMin].parent = i;
tree[i].weight = tree[fristMin].weight+tree[secMin].weight;
tree[i].lchild = fristMin;
tree[i].rchild = secMin;
}
return tree; //返回初始化的哈夫曼树
}
哈夫曼编码（我采用的是从叶子结点–>根节点，所以实际是反过来的）
Char_coding * print_huffmancode(huffmanTree *tree,Char_coding *coding){
// 编码
int ch_length = allchar; //总数
coding = (Char_coding*) malloc(sizeof (Char_coding)*(ch_length));
Char_coding s;
for (int i = 0;i<ch_length;i++) {
int child_curr = i;
int parent_curr = tree[i].parent;
int j = 0; //记录字符的索引
int length_coding =0; //记录编码的长度，在最后设置\000
while (parent_curr != -1) {
if (tree[parent_curr].lchild == child_curr) {
// 左子树设为0
s.Bi_code[j] = '0';
child_curr = parent_curr;
parent_curr = tree[child_curr].parent;
length_coding++;
j++;
} else {
// 右子树设为1
s.Bi_code[j] = '1';
child_curr = parent_curr;
parent_curr = tree[child_curr].parent;
length_coding++;
j++;
}
}
s.ch = tree[i].data;
coding[i] = s;
// 处理串的末尾
coding[i].Bi_code[length_coding] ='\000';
// printf("%d %s\n",i, coding[i].Bi_code);
}
return coding; //返回编码好的哈夫曼编码，从叶子到根节点
}
使用哈夫曼树译码（包括文件保存）
void Decoding(Char_coding *coding,huffmanTree *tree,char *f_name,char *fp_write){
// 译码
FILE *fp1;
FILE *fp_w;
int length = allchar;
fp_w = fopen(fp_write,"w+");
fp1= fopen(f_name,"r");
if(fp1 ==NULL){
printf("译码文件不存在");
}
int root_index = 2*length-2;
int child_root = root_index;
while (!feof(fp1)){
char temp = fgetc(fp1);
if(temp!='\n'){
if(temp == '0'){
child_root = tree[child_root].lchild;
// 找到叶子结点
if(tree[child_root].lchild ==-1 &&tree[child_root].rchild ==-1){
// printf("%c",tree[child_root].data);
fputc(tree[child_root].data,fp_w);
// 回溯到根节点
child_root = root_index;
}
}
else {
if (tree[child_root].rchild != -1) {
child_root = tree[child_root].rchild;
if (tree[child_root].lchild == -1 && tree[child_root].rchild == -1) {
// printf("%c", tree[child_root].data);
fputc(tree[child_root].data,fp_w);
child_root = root_index;
}
}
}
}
else{
continue;
}
}
fclose(fp1);
fclose(fp_w);
}
全部代码（测试文件之类的在下面的链接）
#include <stdio.h>
#include <string.h>
#include <malloc.h>
typedef struct node{
char data;
int weight;
int parent;
int lchild,rchild;
int mark;
}huffmanTree;
typedef struct code_N{
char ch;
char Bi_code[100];
}Char_coding;
typedef struct queue_node{
int data;
struct LinkNode *next;
}LinkNode;
typedef struct queue{
struct queue_node* rear,*front;
}LinkQueue;
int allchar =0; //记录所有字母的个数
void find_min(huffmanTree *tree,int max,int *firstMin,int *secMin){
//查找两个最小的值
int smallindex[2];
for(int j = 0;j<2;j++){
int temp = 9999;
int count = 0;
int final_index =0;
for(int k = 0;k<=max;k++) {
if(tree[k].mark==0){
if(tree[k].weight<temp){
final_index = k;
temp = tree[k].weight;
}
}
else{
count++;
}
// 最后一个结点
if(count ==max &&j ==0){
return ;
}
}
tree[final_index].mark =1;
smallindex[j] = final_index;
}
*firstMin = smallindex[0];
*secMin =smallindex[1];
}
Char_coding * print_huffmancode(huffmanTree *tree,Char_coding *coding){
// 编码
int ch_length = allchar; //总数
coding = (Char_coding*) malloc(sizeof (Char_coding)*(ch_length));
Char_coding s;
for (int i = 0;i<ch_length;i++) {
int child_curr = i;
int parent_curr = tree[i].parent;
int j = 0; //记录字符的索引
int length_coding =0; //记录编码的长度，在最后设置\000
while (parent_curr != -1) {
if (tree[parent_curr].lchild == child_curr) {
// 左子树设为0
s.Bi_code[j] = '0';
child_curr = parent_curr;
parent_curr = tree[child_curr].parent;
length_coding++;
j++;
} else {
// 右子树设为1
s.Bi_code[j] = '1';
child_curr = parent_curr;
parent_curr = tree[child_curr].parent;
length_coding++;
j++;
}
}
s.ch = tree[i].data;
coding[i] = s;
// 处理串的末尾
coding[i].Bi_code[length_coding] ='\000';
// printf("%d %s\n",i, coding[i].Bi_code);
}
return coding; //返回编码好的哈夫曼编码，从叶子到根节点
}
huffmanTree * Init_huffmanTree(huffmanTree *tree,char *ch,int *weight){
int all_node;
int count = strlen(ch);
if(strlen(ch)<0){
return NULL;
}
all_node = 2*count -1;
// 初始化哈夫曼树
tree = (huffmanTree*) malloc((all_node)*sizeof (huffmanTree));
for(int i = 0;i<count;i++){
tree[i].data =ch[i];
tree[i].weight = weight[i];
tree[i].parent =-1;
tree[i].lchild=-1;
tree[i].rchild =-1;
tree[i].mark =0;
}
for(int j = count;j<all_node;j++){
tree[j].data ='#';
tree[j].parent =-1;
tree[j].weight =-1;
tree[j].parent =tree[j].rchild=tree[j].lchild =-1;
tree[j].mark =0;
}
for(int i = count;i<all_node;i++){
int fristMin,secMin;
fristMin = secMin = 0;
find_min(tree,i-1,&fristMin,&secMin); //找到最小索引的两个的下标
tree[fristMin].parent = i;
tree[secMin].parent = i;
tree[i].weight = tree[fristMin].weight+tree[secMin].weight;
tree[i].lchild = fristMin;
tree[i].rchild = secMin;
}
return tree; //返回初始化的哈夫曼树
}
huffmanTree * Init_file_tree(huffmanTree *tree,char* fp_save){
FILE *fp;
fp = fopen(fp_save,"r");
if(fp ==NULL){
printf("初始化文件不存在:%s",fp_save);
exit(0);
}
int count = 0;
while(!feof(fp)){
char temp[200];
fgets(temp,200,fp);
count++;
}
// 根据文件进行初始化
fclose(fp);
tree = (huffmanTree *) malloc(sizeof (huffmanTree)*(count-1));
fp = fopen(fp_save,"r");
for(int i = 0;i<count-1;i++){
fscanf(fp,"%c,%d,%d,%d,%d,%d\n",&tree[i].data,&tree[i].weight,
&tree[i].parent,&tree[i].lchild,&tree[i].rchild,&tree[i].mark);
}
allchar = (count+1)/2;
// printf("%c",tree[0].data);
return tree; //返回初始化的哈夫曼树
}
void set_tree(huffmanTree *tree,char *file_save){
int length = allchar;
int node_len = 2*length -1;
FILE *fp_save;
fp_save = fopen(file_save,"w+");
if (fp_save==NULL){
printf("文件打开错误");
exit(0);
}
for(int i = 0; i<node_len;i++){
fprintf(fp_save,"%c,%d,%d,%d,%d,%d\n",tree[i].data,tree[i].weight,tree[i].parent,tree[i].lchild,tree[i].rchild,tree[i].mark);
// printf("%c %d %d %d %d\n",tree[i].data,tree[i].parent,tree[i].lchild,tree[i].rchild,tree[i].mark);
}
fclose(fp_save);
}
void seting_file(Char_coding *coding,huffmanTree *tree,char *word,char *f_name){
// 保存目标文本编码到文件
int length = allchar;
int char_length = strlen(word);
FILE *fp;
fp = fopen(f_name,"w+");
if(fp==NULL){
printf("文件打开错误");
exit(0);
}
unsigned long count_line = 0;
for(int i = 0;i<char_length;i++){
for(int j = 0;j<length;j++){
if(coding[j].ch == word[i]){
for(int k =strlen(coding[j].Bi_code)-1;k>=0;k--){
// printf("%c",coding[j].Bi_code[k]);
fputc(coding[j].Bi_code[k],fp);
// 在写入文件时50个换行
// if((count_line+1)%50==0){
// fputc('\n',fp);
// }
count_line++;
}
break;
}
}
}
fclose(fp);
}
void Decoding(Char_coding *coding,huffmanTree *tree,char *f_name,char *fp_write){
// 译码
FILE *fp1;
FILE *fp_w;
int length = allchar;
fp_w = fopen(fp_write,"w+");
fp1= fopen(f_name,"r");
if(fp1 ==NULL){
printf("译码文件不存在");
}
int root_index = 2*length-2;
int child_root = root_index;
while (!feof(fp1)){
char temp = fgetc(fp1);
if(temp!='\n'){
if(temp == '0'){
child_root = tree[child_root].lchild;
// 找到叶子结点
if(tree[child_root].lchild ==-1 &&tree[child_root].rchild ==-1){
// printf("%c",tree[child_root].data);
fputc(tree[child_root].data,fp_w);
// 回溯到根节点
child_root = root_index;
}
}
else {
if (tree[child_root].rchild != -1) {
child_root = tree[child_root].rchild;
if (tree[child_root].lchild == -1 && tree[child_root].rchild == -1) {
// printf("%c", tree[child_root].data);
fputc(tree[child_root].data,fp_w);
child_root = root_index;
}
}
}
}
else{
continue;
}
}
fclose(fp1);
fclose(fp_w);
}
//入队
void InQueue(LinkQueue *queue,int x){
//生成新节点
LinkNode *p = (LinkNode*) malloc(sizeof (LinkNode*));
p->data = x;
p->next = NULL;
if(queue->front ==NULL){
queue->front = queue->rear = p;
}
else {
queue->rear->next = p;
queue->rear = p;
}
}
//出队列
int DeQueue(LinkQueue *queue){
if(queue->front ==NULL){
return 0;
}
LinkNode *p = queue->front;
int temp = p->data; //保存出队列的值
queue->front = p->next;
// free(p);
return temp;
}
void init_queue(LinkQueue *queue){
queue->front = queue->rear =NULL;
}
void traverse_tree(huffmanTree*tree){
// 层次遍历
LinkQueue queue;
init_queue(&queue);
int length = allchar;
int all_node = 2*length-1;
int count = all_node;
int root_index = all_node-1;
int ceng_index = root_index;
int cennum =1;
printf("下面是按照凹入表示法打印的哈夫曼树");
while(count>0){
for(int i = 0;i<cennum;i++){
printf("-");
}
printf("%c\n",tree[root_index].data);
count--;
int l_child_index = tree[root_index].lchild;
int right_index = tree[root_index].rchild;
if(l_child_index!=-1){
InQueue(&queue,l_child_index);
}
if(ceng_index == root_index){
cennum++;
// printf("\n");
if(l_child_index !=-1 &&right_index !=-1 ){
ceng_index = right_index;
}
else if(l_child_index ==-1 && right_index !=-1){
ceng_index = right_index;
}
else if(l_child_index !=-1&& right_index ==-1){
ceng_index = l_child_index;
}
else{
ceng_index = tree[tree[tree[root_index].parent].lchild].rchild;
}
}
if(right_index!=-1){
InQueue(&queue,right_index);
}
root_index = DeQueue(&queue);
}
}
void showface() {
printf("\n\n");
printf("\t\t\t====================哈夫曼树译码系统====================\n");
printf("\t\t\t* *\n");
printf("\t\t\t* 1>.初始化哈夫曼树 \n");
printf("\t\t\t* 2>. 编码\n");
printf("\t\t\t* 3>. 译码\n");
printf("\t\t\t* 4>. 打印字符编码文件信息\n");
printf("\t\t\t* 5>. 打印哈夫曼树\n");
printf("\t\t\t* 0>. 退出本系统\n");
printf("\t\t\t* 欢迎使用本系统!\n\n");
printf("\t\t\t=========================================================\n");
}
huffmanTree * input_data(huffmanTree *tree){
int num;
printf("请输入字符总数\n");
scanf("%d",&num);
allchar = num;
int weight[27] = {186, 64, 13, 22, 32, 103, 21,15, 47, 57 ,1 ,5, 32,20 ,57, 63, 15, 1 ,48 ,51, 80, 23 ,8, 18 ,1, 16, 1};
char ch[27][2] = {' ','A','B','C','D','E','F','G','H','I','J','K','L','M','N','O','P','Q','R','S','T','U','V','W','X','Y','Z'};
tree= Init_huffmanTree(&tree,ch,&weight); //初始化哈夫曼树
return tree;
}
void printf_code_print(char *filename){
FILE *fp;
fp = fopen(filename,"r");
if(fp==NULL){
printf("文件不存在");
exit(0);
}
int count=0;
while(!feof(fp)){
char temp = fgetc(fp);
if(temp !=EOF){
printf("%c",temp);
}
if((count+1)%50 ==0){
printf("\n");
}
count++;
}
}
int main() {
int button;
huffmanTree *tree;
char word[200];
int num;
Char_coding *coding;
int isinit = 0;
char fp_save[200] ="../save_tree.txt";
char fp [200]="../codeing.txt";
char fp_w [200] = "../textfile.txt";
do {
showface();
printf("请输入相应的数字，进行相应的操作:\n");
scanf("%d", &button);
switch (button) {
case 1:
tree = input_data(&tree);
set_tree(tree,fp_save);
isinit =1;
break;
case 2:
if(isinit ==0){
isinit =1;
tree = Init_file_tree(&tree,fp_save);
}
printf("请输入你想要编码的字符串\n");
scanf("%s",word);
coding =print_huffmancode(tree,&coding);
seting_file(coding,tree,word,fp);
break;
case 3:
if(isinit ==0){
isinit =1;
tree = Init_file_tree(&tree,fp_save);
}
Decoding(coding,tree,fp,fp_w);
break;
case 4:
if(isinit ==0){
isinit =1;
tree = Init_file_tree(&tree,fp_save);
}
printf_code_print(fp);
break;
case 5:
if(isinit ==0){
isinit =1;
tree = Init_file_tree(&tree,fp_save);
}
traverse_tree(tree);
break;
case 0:
printf("即将退出.....");
exit(0);
default:
printf("您输入的指令不正确，请重新输入");
break;
}
printf("\n\n");
} while (button);
return 0;
}
源码及文件
链接：https://pan.baidu.com/s/154ub53uLrhoXN4IYwn5gUw
提取码：1314
总结
上述是哈夫曼树的编码和译码过程，本文的字母是自己已经固定了，但是基本不变，本人是菜鸡一枚，需要的可以自取，如果有问题，可以在评论区交流，或者私信我。
数据结构哈夫曼树（C语言版）的更多相关文章
- 数据结构-哈夫曼树（python实现）
好,前面我们介绍了一般二叉树.完全二叉树.满二叉树,这篇文章呢,我们要介绍的是哈夫曼树. 哈夫曼树也叫最优二叉树,与哈夫曼树相关的概念还有哈夫曼编码,这两者其实是相同的.哈夫曼编码是哈夫曼在1952年 ...
- C#数据结构-赫夫曼树
什么是赫夫曼树? 赫夫曼树(Huffman Tree)是指给定N个权值作为N个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小.哈夫曼树(也称为最优二叉树)是带权路径长度最短的树,权值较大的结点 ...
- Java数据结构和算法（四）赫夫曼树
Java数据结构和算法(四)赫夫曼树 数据结构与算法目录(https://www.cnblogs.com/binarylei/p/10115867.html) 赫夫曼树又称为最优二叉树,赫夫曼树的一个 ...
- 6-9-哈夫曼树（HuffmanTree）-树和二叉树-第6章-《数据结构》课本源码-严蔚敏吴伟民版
课本源码部分 第6章 树和二叉树 - 哈夫曼树(HuffmanTree) ——<数据结构>-严蔚敏.吴伟民版 源码使用说明 链接☛☛☛ <数据结构-C语言版> ...
- Android版数据结构与算法(七):赫夫曼树
版权声明:本文出自汪磊的博客,未经作者允许禁止转载. 近期忙着新版本的开发,此外正在回顾C语言,大部分时间没放在数据结构与算法的整理上,所以更新有点慢了,不过既然写了就肯定尽力将这部分完全整理好分享出 ...
- 数据结构之C语言实现哈夫曼树
1.基本概念 a.路径和路径长度 若在一棵树中存在着一个结点序列 k1,k2,……,kj, 使得 ki是ki+1 的双亲(1<=i<j),则称此结点序列是从 k1 到 kj 的路径. 从 ...
- C语言数据结构之哈夫曼树及哈夫曼编码的实现
代码清单如下: #pragma once #include<stdio.h> #include"stdlib.h" #include <string.h> ...
- 哈夫曼树(一)之 C语言详解
本章介绍哈夫曼树.和以往一样,本文会先对哈夫曼树的理论知识进行简单介绍,然后给出C语言的实现.后续再分别给出C++和Java版本的实现:实现的语言虽不同,但是原理如出一辙,选择其中之一进行了解即可.若 ...
- 数据结构图文解析之：哈夫曼树与哈夫曼编码详解及C++模板实现
0. 数据结构图文解析系列 数据结构系列文章 数据结构图文解析之:数组.单链表.双链表介绍及C++模板实现 数据结构图文解析之:栈的简介及C++模板实现 数据结构图文解析之:队列详解与C++模板实现 ...
- 【数据结构】赫夫曼树的实现和模拟压缩(C++)
赫夫曼(Huffman)树,由发明它的人物命名,又称最优树,是一类带权路径最短的二叉树,主要用于数据压缩传输. 赫夫曼树的构造过程相对比较简单,要理解赫夫曼数,要先了解赫夫曼编码. 对一组出现频率不同 ...
随机推荐
- TP5.0--5.1获取当前域名的方法
TP5.0获取当前域名的方法 use think\Request; $request = Request::instance(); $domain = $request->domain(); 获 ...
- （Winform程序带源码） 弹出输入框和获取输入框的值
弹出输入框和获取输入框的值: private void button1_Click(object sender, EventArgs e) { string returnValue = Microso ...
- 在Vim编辑器中查找选定文本
按照任意选定文本查找: 1. 进入visiual模式选定文本, 按 y 键复制: 2. 按 / 键进入查找模式: 3. 按 Ctrl + r 打开vim寄存器: 4. 按 " 键将寄存器内容 ...
- 打开CMD方式
打开CMD的方式 win+r 输入cmd 常用的Dos命令 1.#盘符切换2.#查看当前文件目录下的所有文件 dir3.#切换目录 cd change directory4.#cd .. 返回上级5. ...
- 2-2 理解const
1 const 在引用中注意不能为常量绑定一个非常量的引用 在指针中区分low-level const和top-level const const通常用于定义常量,一经定义不许修改,且使用const必 ...
- SpringBoot使用OkHttp
参考文章: https://www.cnblogs.com/hongdada/p/9259965.html https://blog.csdn.net/qq_41890954/article/deta ...
- Python自动化环境搭建轻轻松松---selenium
其实安装selenium实现自动化搭建环境也不拿 一共四步 1.Python开发环境 2.安装selenium包 3.安装浏览器 4.安装你安装的浏览器驱动 一: 想要实现Python环境不可能缺席: ...
- springboot--yaml数据读取的三种方式
结果:
- C++类的构造函数、析构函数、拷贝构造函数、赋值函数和移动构造函数详细总结
目录 1. 五种函数介绍 2. 左值&右值怎么区分?怎么看? 3. 匿名对象的3种使用情况 4. 代码详细验证每个函数调用情况 4.1 测试 f_1 函数(函数形参测试 -- 值传递) 4.2 ...
- Dubbo服务提供者如何优雅升级？
文章首发于公众号:BiggerBoy.欢迎关注. 往期文章推荐 大坑!隐式转换导致索引失效...高性能分布式限流:Redis+Lua真香!MySQL索引知识点&常见问题汇总联合索引在B+树上的 ...