寻找第K小元素

要在一个序列里找出第K小元素，可以用排序算法，然后再找。可以证明，排序算法的上界为O(nlogn)。

在这里，给出两种可以在线性时间内找出第K小元素的方法。

方法1：

(1) 选定一个比较小的阈值（如44），当序列元素小于阈值时，直接用排序算法来做；

(2) 当序列元素大于阈值时，把元素划分为以5个元素为一组，每一组元素自身作排序，然后挑出每一组元素的中间值，再在所有的中间值中，递归调用本算法，挑出中间值，可以认为，此值大约为整个序列的中间值（当序列元素个数不是5的倍数时，最后一组不足5的舍掉，这个对中间值影响不大）；

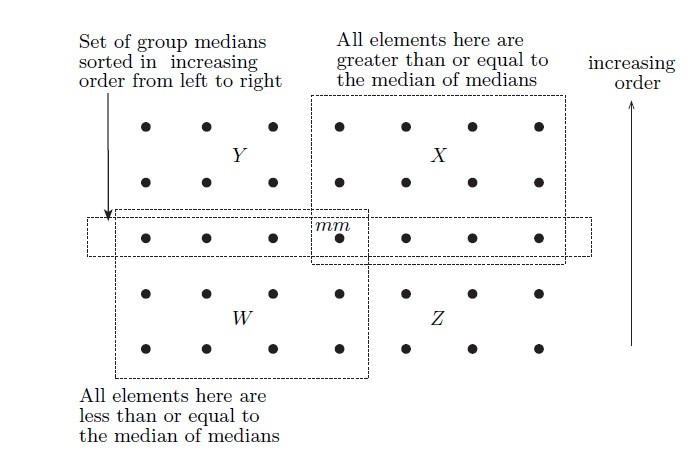
（图片参考《ALGORITHMS DESIGN TECHNIQUES AND ANALYSIS》 M. H. Alsuwaiyel）

(3) 把元素按中间值划分为三组，第一组小于中间值，第二组等于中间值，第三组大于中间值；

(4) 若第一组的元素个数大于等于K，即第K个元素在第一组内；若第一组和第二组的元素个数大于等于K，即中间值为第K个元素；否则，第K个元素在第三组，再递归调用本算法，注意K要减去一二组的元素个数。

    public static int select(int[] A, int k){
        return selectDo(A, 0, A.length-1, k);
    }

    private static int selectDo(int[] A, int low, int high, int k){
        //select k min number
        int p = high - low + 1;
        if(p < 44){
            Arrays.sort(A, low, high+1);
            return A[low+k];
        }
        //A divided into q groups, each group 5 elements, and sort them
        int q = p/5;
        int[] M = new int[q];
        for(int i = 0; i < q; i ++){
            Arrays.sort(A, low + 5*i, low + 5*i + 5);
            M[i] = A[low+5*i+2];
        }
        //select mid in M
        int mid = selectDo(A, 0, q-1, (q-1)/2);
        //A divided into 3 groups
        int[] A1 = new int[p];
        int[] A2 = new int[p];
        int[] A3 = new int[p];
        int count1, count2, count3;
        count1 = count2 = count3 = 0;
        for(int i = low; i <= high; i ++){
            if(A[i] < mid)
                A1[count1++] = A[i];
            else if(A[i] == mid)
                A2[count2++] = A[i];
            else
                A3[count3++] = A[i];
        }
        if(count1 >= k)
            return selectDo(A1, 0, count1-1, k);
        if(count1 + count2 >= k)
            return mid;
        return selectDo(A3, 0, count3-1, k-count1-count2);
    }

Java

这个方法虽然可以以最坏时间复杂度O(n)，但是系数值会比较大，而且算法比较复杂。

方法2：

(1) 随机挑选一个元素X作为数组的划分，此时数组分为三部分，第一部分是小于X的元素，第二部分只有一个元素就是X，第三部分是大于或等于X的元素；

(2) 当第一部分的元素个数N大于K时，说明第K个元素在第一部分；当第一部分的元素个数N等于K时，说明X就是第K个元素（注意到下标从0开始）；否则，第K个元素在第三部分，再递归调用本算法，注意K要减去第一部分的元素个数再减1（包括X）。

    public static int randomSelect(int[] A, int k){
        return randomSelectDo(A, 0, A.length-1, k);
    }

    private static int randomSelectDo(int[] A, int low, int high, int k){
        int i = randomPartition(A, low, high);
        //n is the number of < A[i]
        int n = i-low;
        if(n > k)
            return randomSelectDo(A, low, i-1, k);
        else if(n == k)
            return A[i];
        else
            return randomSelectDo(A, i+1, high, k-n-1);
    }

    private static void swap(int[] A, int i, int j){
        int temp = A[i];
        A[i] = A[j];
        A[j] = temp;
    }

    private static int randomPartition(int[] A, int low, int high){
        //random divide
        Random rand = new Random();
        int r = rand.nextInt(high-low+1) + low;
        swap(A, low, r);
        int i = low;
        int x = A[low];
        for(int j = low+1; j <= high; j ++){
            if(A[j] < x){
                i ++;
                if(i != j){
                    swap(A, i, j);
                }
            }
        }
        swap(A, low, i);
        return i;
    }

Java

此方法和快速排序有点相似，也是需要划分数组的方法；与方法1相比，不同之处在于划分元素的选择。采用随机化划分，在实际上可以达到O(n)的要求。而且算法简洁优美。