Floyd-Warshall求图中任意两点的最短路径

原创

---

　　除了DFS和BFS求图中最短路径的方法，算法Floyd-Warshall也可以求图中任意两点的最短路径。

　　从图中任取两点A、B，A到B的最短路径无非只有两种情况：

　　1：A直接到B这条路径即是最短路径（前提是存在此路径）；

　　2：A先通过其他点，再由其他点到B。

　　我们并不知道A是否需要通过其他点间接到达B，所以只能比较，用A到B的直接路径和A先通过其他点

再间接到达B的路径长度进行比较，然后更新为较小值。

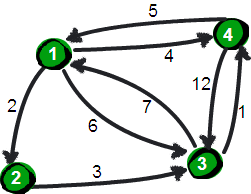
　　上图中若要求顶点4到顶点3的最短路径，可以比较顶点4直接到3的路径和顶点4先到1，再到3的路径。

更新为最小值，此时邻接矩阵matrix[4][3]存储的即为借用了顶点1后4到3的最短路径；然后再借用了1的

基础上再借用顶点2，此时再次比较matrix[4][3]和matrix[4][2]+matrix[2][3]，更新为最小值；比较完

毕后matrix[4][3]乃存储了最短路径，求其他任意两点也是如此。

　　总结一下，求图中任意两点的最短路径，通过比较一次取一个其他顶点间接到达的最短路径和直接路径

进行比较，更新为最小值即可。

import java.util.*;

public class Floyd_Warshall {

    static int v;    //顶点
    static int e;    //边
    static int matrix[][];

    public static void main(String args[]) {
        Scanner reader=new Scanner(System.in);
        v=reader.nextInt();
        e=reader.nextInt();
        matrix=new int[v+1][v+1];    //编号从1开始
        //矩阵初始化
        for(int i=1;i<=v;i++) {
            for(int j=1;j<=v;j++) {
                if(i==j) {    //顶点本身
                    matrix[i][j]=0;
                }
                else {    //无穷
                    matrix[i][j]=99999;
                }
            }
        }
        //读入边
        for(int i=1;i<=e;i++) {
            int first_City=reader.nextInt();
            int second_City=reader.nextInt();
            int value=reader.nextInt();
            matrix[first_City][second_City]=value;    //有向图
        }
        for(int k=1;k<=v;k++) {    //只允许经过顶点k
            for(int i=1;i<=v;i++) {
                for(int j=1;j<=v;j++) {
                    if(matrix[i][k]+matrix[k][j]<matrix[i][j]) {
                        matrix[i][j]=matrix[i][k]+matrix[k][j];
                    }
                }
            }
        }
        for(int i=1;i<=v;i++) {
            for(int j=1;j<=v;j++) {
                System.out.print(matrix[i][j]+" ");
            }
            System.out.println();
        }
    }
}

测试用例：

输入：

4 8

1 2 2

2 3 3

3 4 1

4 3 12

1 3 6

3 1 7

1 4 4

4 1 5

输出：

0 2 5 4 

9 0 3 4 

6 8 0 1 

5 7 10 0 

12:30:24

2018-07-28