【BZOJ2045】双亲数 莫比乌斯反演

【BZOJ2045】双亲数

Description

小D是一名数学爱好者，他对数字的着迷到了疯狂的程度。 我们以d = gcd(a, b)表示a、b的最大公约数，小D执著的认为，这样亲密的关系足可以用双亲来描述，此时，我们称有序数对(a, b)为d的双亲数。 与正常双亲不太相同的是，对于同一个d，他的双亲太多了 >_< 比如，(4, 6), (6, 4), (2, 100)都是2的双亲数。 于是一个这样的问题摆在眼前，对于0 < a <= A, 0 < b <= B，有多少有序数对(a, b)是d的双亲数？

Input

输入文件只有一行，三个正整数A、B、d (d <= A, B)，意义如题所示。

Output

输出一行一个整数，给出满足条件的双亲数的个数。

Sample Input

5 5 2

Sample Output

3
【样例解释】

满足条件的三对双亲数为(2, 2) (2, 4) (4, 2)

HINT

对于100%的数据满足0 < A, B < 10^ 6

题解：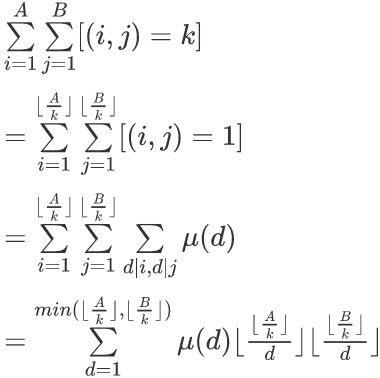

总之就是一旦看到[...=1]就往反演上想就好了

#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
const int maxn=1000010;
int n,m,d,num;
int pri[maxn],mu[maxn],sm[maxn];
bool np[maxn];
typedef long long ll;
ll ans;
int main()
{
	scanf("%d%d%d",&n,&m,&d),n/=d,m/=d;
	if(n<m)	swap(n,m);
	int i,j,last;
	sm[1]=mu[1]=1;
	for(i=2;i<=n;i++)
	{
		if(!np[i])	pri[++num]=i,mu[i]=-1;
		sm[i]=sm[i-1]+mu[i];
		for(j=1;j<=num&&i*pri[j]<=n;j++)
		{
			np[i*pri[j]]=1;
			if(i%pri[j]==0)
			{
				mu[i*pri[j]]=0;
				break;
			}
			mu[i*pri[j]]=-mu[i];
		}
	}
	for(i=1;i<=m;i=last+1)
	{
		last=min(n/(n/i),m/(m/i));
		ans+=1ll*(sm[last]-sm[i-1])*(n/i)*(m/i);
	}
	printf("%lld",ans);
	return 0;
}