POJ 3734 生成函数
题意:一排n长度的砖,有四种颜色,红色绿色是偶数,有少染色方式。
分析:
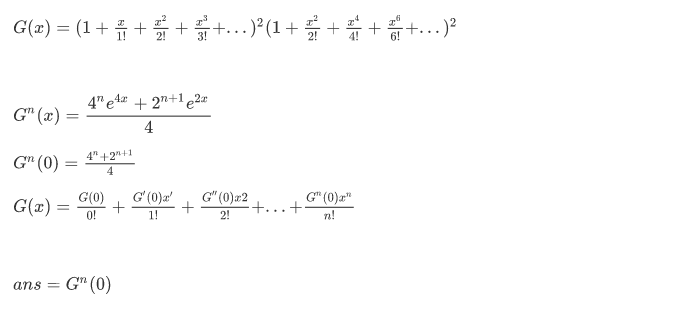
泰勒展开式:
chx = (e^x+e^(-x))/2 = 1 + x^2/2! + x^4/4! + x^6/6! + ... ...
shx = (e^x-e^(-x))/2 = x + x^3/3! + x^5/5! + x^7/7! + ... ...
POJ 3734 生成函数的更多相关文章
- poj 3734 Blocks【指数型生成函数】
指数型生成函数,推一推可得: \[ (1+\frac{x^1}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+...)^2+(1+\frac{x^2}{2!}+\frac{x^4 ...
- [POJ 3734] Blocks (矩阵高速幂、组合数学)
Blocks Time Limit: 1000MS Memory Limit: 65536K Total Submissions: 3997 Accepted: 1775 Descriptio ...
- poj 3734 Blocks
ゲート 分析:这题过的人好多,然后大家好像是用矩阵过的(((φ(◎ロ◎;)φ))).我自己是推公式的. 对于任意的有这个式子, 就是先从里面选偶数个涂成两个指定的颜色,再在选出的里面选定涂某种颜色,选 ...
- poj 3734 Blocks 快速幂+费马小定理+组合数学
题目链接 题意:有一排砖,可以染红蓝绿黄四种不同的颜色,要求红和绿两种颜色砖的个数都是偶数,问一共有多少种方案,结果对10007取余. 题解:刚看这道题第一感觉是组合数学,正向推了一会还没等推出来队友 ...
- poj 3734 矩阵快速幂+YY
题目原意:N个方块排成一列,每个方块可涂成红.蓝.绿.黄.问红方块和绿方块都是偶数的方案的个数. sol:找规律列递推式+矩阵快速幂 设已经染完了i个方块将要染第i+1个方块. a[i]=1-i方块中 ...
- POJ 3734
题目的大意: 给定待粉刷的n个墙砖(排成一行),每一个墙砖能够粉刷的颜色种类为:红.蓝.绿.黄, 问粉刷完成后,红色墙砖和蓝色墙砖都是偶数的粉刷方式有多少种(结果对10007取余). 解题思路: 思路 ...
- Blocks(POJ 3734 矩阵快速幂)
Blocks Input The first line of the input contains an integer T(1≤T≤100), the number of test cases. E ...
- poj 3734 方块涂色 求红色 绿色方块都为偶数的方案数 (矩阵快速幂)
N个方块排成一列 用红,蓝,绿,黄4种颜色去涂色,求红色方块 和绿色方块个数同时为偶数的 方案数 对10007取余 Sample Input 212Sample Output 2//(蓝,黄)6//( ...
- POJ 3734 Blocks (矩阵快速幂)
题目链接 Description Panda has received an assignment of painting a line of blocks. Since Panda is such ...
随机推荐
- CentOS 6.2出现Disk sda contains BIOS RAID metadata解决方法
今天在安装CentOS 6.2的时候,当进到检测硬盘的时候,总是过不去,报错如下: Disk sda contains BIOS RAID metadata, but is not part of a ...
- Vue 项目启动抛出 Error/ No PostCSS Config found in
项目启动时抛出 Error: No PostCSS Config found in … 的错误表示某个 css 文件不能被引入 解决办法: module.exports = { plugins: { ...
- NFS 优化及详解
一, 启动过程: 所以启动的时候一定一定要先启用——————rpcbind———————————————— 启动 rpcbind ------>/etc/init.d/rpcbind rest ...
- c#字典排序
using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.T ...
- React.js 小书 Lesson15 - 实战分析:评论功能(二)
作者:胡子大哈 原文链接:http://huziketang.com/books/react/lesson15 转载请注明出处,保留原文链接和作者信息. 上一节我们构建了基本的代码框架,现在开始完善其 ...
- BNU29139——PvZ once again——————【矩阵快速幂】
PvZ once again Time Limit: 2000ms Memory Limit: 65536KB 64-bit integer IO format: %lld Java cla ...
- 在List中常用的linq表达式
为了下面举例方便,先声明一个集合: public List<Model.Resume> GetResumeList() { var list = new List<Model.Res ...
- javaSystem.out.println()输出byte[]和char[]异常的问题
javaSystem.out.println()输出byte[]和char[]异常的问题 今天 突然有人问我他写的byte[]和char[],在用System.out.println()输出的时候所得 ...
- Drupal theme_hook
模板语言和主题引擎 用Drupal的行话来说,主题就是一组负责你站点外观的文件.你可以从http://drupal.org/project/Themes下载第 3方主题,或者你可以自己动手创建一个主题 ...
- 使用cookie实现只出现一次的广告代码效果
我们上网经常会遇到第一次需要登录而之后不用再登录的网站的情况,其实是运用了Cookie 存储 web 页面的用户信息,Cookie 以名/值对形式存储,当浏览器从服务器上请求 web 页面时, 属于该 ...
