UVa 10870 Recurrences (矩阵快速幂)

题意：给定 d , n , m (1<=d<=15,1<=n<=2^31-1,1<=m<=46340)。a1 , a2 ..... ad。f(1), f(2) ..... f(d)，求 f(n) = a1*f(n-1) + a2*f(n-2) +....+ ad*f(n-d)，计算f(n) % m。

析：很明显的矩阵快速幂，构造矩阵，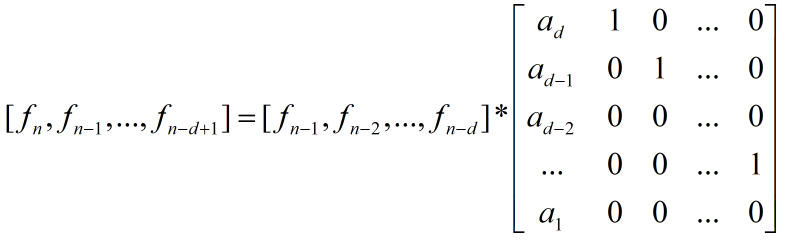

，然后后面的就很简单了。

代码如下：

#pragma comment(linker, "/STACK:1024000000,1024000000")
#include <cstdio>
#include <string>
#include <cstdlib>
#include <cmath>
#include <iostream>
#include <cstring>
#include <set>
#include <queue>
#include <algorithm>
#include <vector>
#include <map>
#include <cctype>
#include <cmath>
#include <stack>
#include <sstream>
#include <list>
#include <assert.h>
#include <bitset>
#include <numeric>
#define debug() puts("++++")
#define gcd(a, b) __gcd(a, b)
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define fi first
#define se second
#define pb push_back
#define sqr(x) ((x)*(x))
#define ms(a,b) memset(a, b, sizeof a)
#define sz size()
#define pu push_up
#define pd push_down
#define cl clear()
#define lowbit(x) -x&x
//#define all 1,n,1
#define FOR(i,n,x)  for(int i = (x); i < (n); ++i)
#define freopenr freopen("in.in", "r", stdin)
#define freopenw freopen("out.out", "w", stdout)
using namespace std;

typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> P;
const int INF = 0x3f3f3f3f;
const LL LNF = 1e17;
const double inf = 1e20;
const double PI = acos(-1.0);
const double eps = 1e-8;
const int maxn = 20 + 10;
const int maxm = 1e6 + 2;
const LL mod = 1000000007;
const int dr[] = {-1, 1, 0, 0, 1, 1, -1, -1};
const int dc[] = {0, 0, 1, -1, 1, -1, 1, -1};
const char *de[] = {"0000", "0001", "0010", "0011", "0100", "0101", "0110", "0111", "1000", "1001", "1010", "1011", "1100", "1101", "1110", "1111"};
int n, m;
const int mon[] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
const int monn[] = {0, 31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
inline bool is_in(int r, int c) {
  return r >= 0 && r < n && c >= 0 && c < m;
}

struct Matrix{
  int a[15][15], n;
  void init(){  ms(a, 0); }
  void toOne(){ FOR(i, n, 0)  a[i][i] = 1; }
  Matrix operator * (const Matrix &rhs){
    Matrix res;  res.n = n;  res.init();
    FOR(i, n, 0)  FOR(j, n, 0)  FOR(k, n, 0)
      res.a[i][j] = (res.a[i][j] + (LL)a[i][k] * rhs.a[k][j]) % m;
    return res;
  }
};

Matrix fast_pow(Matrix x, int n){
  Matrix res;  res.n = x.n;  res.init(); res.toOne();
  while(n){
    if(n&1)  res = res * x;
    x = x * x;
    n >>= 1;
  }
  return res;
}

int main(){
  int d;
  while(scanf("%d %d %d", &d, &n, &m) == 3 && n+m+d){
    Matrix x, y;  x.init();  y.init();
    x.n = y.n = d;
    for(int i = 0; i < d; ++i){
      scanf("%d", &y.a[i][0]);
      y.a[i][0] %= m;
    }
    for(int i = d-1; i >= 0; --i){
      scanf("%d", &x.a[0][i]);
      x.a[0][i] %= m;
    }
    if(n <= d){ printf("%d\n", x.a[0][d-n]);  continue; }
    for(int i = 0; i + 1 < d; ++i)  y.a[i][i+1] = 1;
    Matrix ans = x * fast_pow(y, n - d);
    printf("%d\n", ans.a[0][0]);
  }
  return 0;
}