HDU2552 三足鼎立 【数学推理】

三足鼎立

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)

Total Submission(s): 2406    Accepted Submission(s): 1335

Problem Description

MCA山中人才辈出，洞悉外界战火纷纷，山中各路豪杰决定出山解救百姓于水火，曾以题数扫全场的威士忌，以前高数九十九的天外来客。曾以一剑铸十年的亦纷菲，歃血为盟，盘踞全国各个要塞（简称全国赛）遇敌杀敌，遇佛杀佛，最终击退辽军。临时平定外患，三人位置也处于稳态。

可惜辽誓不甘心，辽国征南大将军<耶律javac++>欲找出三人所在逐个击破，如今他发现威士忌的位置s,天外来客的位置u，只是非常难探查到亦纷菲v所在何处，仅仅能知道三人满足关系：



arctan(1/s) = arctan(1/u)+arctan(1/v)



注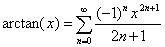：(当中0 <= x <= 1)

定义 f(s, u, v) = v*u-s*u-s*v 的值 为<三足鼎立>



<耶律javac++>想计算<三足鼎立>的值

 

Input

首先输入一个t,表示有t组数据，跟着t行：

输入s, u (s <= 12^3, u <= 2^20 且 s, u, v > 0)

且s,u,v均为实数

 

Output

输出 v*u-s*u-s*v 的值，为了简单起见，假设是小数，直接取整



比方：答案是1.7 则输出 1

 

Sample Input

1
1 2

 

Sample Output

1

 

Author

英雄哪里出来

 

Source

field=problem&key=2008%A1%B0%E7%CD%B7%D7%CF%C2%C9%B3%D0%A3%D4%B0%CE%C4%BB%AF%BB%EE%B6%AF%D4%C2%A1%B1%D6%AE%B4%F3%D1%A7%C9%FA%B3%CC%D0%F2%C9%E8%BC%C6%BE%BA%C8%FC%F4%DF%D0%C2%C9%FA%D7%A8%B3%A1&source=1&searchmode=source">2008“缤纷下沙校园文化活动月”之大学生程序设计竞赛暨新生专场

借用讨论区大牛的推导过程：

1.tan(a+b) = ( tan(a) + tan(b) ) / (1 – tan(a) * tan(b) )
2.tan( atan(x) ) = x
arctan(1/s) = arctan(1/u)+arctan(1/v)
所以得1/s = tan( arctan(1/u)+arctan(1/v) ) = (tan(arctan(1/u)) + tan(arctan(1/v)))/(1-tan(arctan(1/u))*tan(arctan(1/v))) = (1/u + 1/v) / (1 - 1/(uv))
所以解得 uv = 1 + us + vs
所以v*u-s*u-s*v恒等于1

#include <stdio.h>

int main() {
	int t;
	scanf("%d", &t);
	while(t--) {
		scanf("%*d%*d");
		printf("1\n");
	}
	return 0;
}