stacking过程

图解stacking原理：

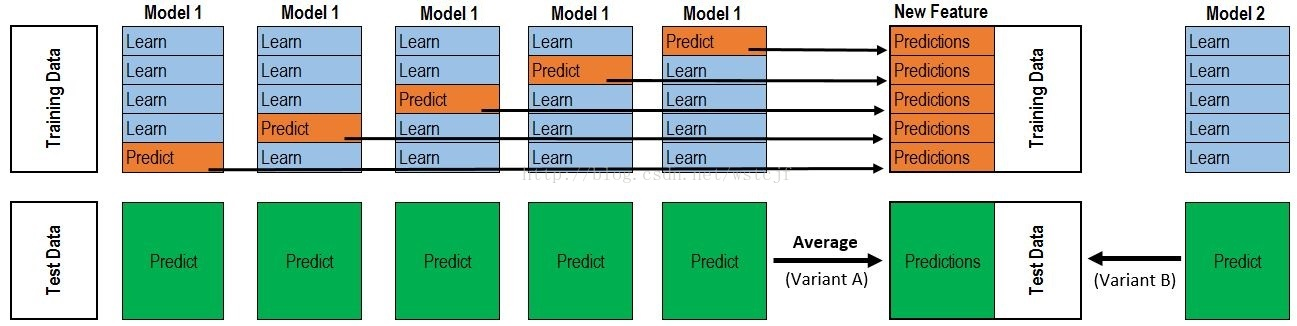
上半部分是用一个基础模型进行5折交叉验证，如：用XGBoost作为基础模型Model1，5折交叉验证就是先拿出四折作为training data，另外一折作为testing data。注意：在stacking中此部分数据会用到整个traing set。如：假设我们整个training set包含10000行数据，testing set包含2500行数据，那么每一次交叉验证其实就是对training set进行划分，在每一次的交叉验证中training data将会是8000行，testing data是2000行。

每一次的交叉验证包含两个过程，1. 基于training data训练模型；2. 基于training data训练生成的模型对testing data进行预测。在整个第一次的交叉验证完成之后我们将会得到关于当前testing data的预测值，这将会是一个一维2000行的数据，记为a1。注意！在这部分操作完成后，我们还要对数据集原来的整个testing set进行预测，这个过程会生成2500个预测值，这部分预测值将会作为下一层模型testing data的一部分，记为b1。因为我们进行的是5折交叉验证，所以以上提及的过程将会进行五次，最终会生成针对testing set数据预测的5列2000行的数据a1,a2,a3,a4,a5，对testing set的预测会是5列2500行数据b1,b2,b3,b4,b5。

在完成对Model1的整个步骤之后，我们可以发现a1,a2,a3,a4,a5其实就是对原来整个training set的预测值，将他们拼凑起来，会形成一个10000行一列的矩阵，记为A1。而对于b1,b2,b3,b4,b5这部分数据，我们将各部分相加取平均值，得到一个2500行一列的矩阵，记为B1。

以上就是stacking中一个模型的完整流程，stacking中同一层通常包含多个模型，假设还有Model2: LR，Model3：RF，Model4: GBDT，Model5：SVM，对于这四个模型，我们可以重复以上的步骤，在整个流程结束之后，我们可以得到新的A2,A3,A4,A5,B2,B3,B4,B5矩阵。

在此之后，我们把A1,A2,A3,A4,A5并列合并得到一个10000行五列的矩阵作为training data，B1,B2,B3,B4,B5并列合并得到一个2500行五列的矩阵作为testing data。让下一层的模型，基于他们进一步训练。

如何实现？

1.写代码自己实现

2.如果嫌麻烦可以调用API

code1：

from vecstack import stacking

# 输入数据

# 初始化第一层评估器
models = [LinearRegression(),
          Ridge(random_state=0)]

# 把 stack特征排成一列
S_train, S_test = stacking(models, X_train, y_train, X_test, regression=True, verbose=2)

# 如果觉得效果可以在提升，我们可以使用第一层提取的stack特征输入到模型中

code2：

from vecstack import StackingTransformer

estimators = [('lr', LinearRegression()),
              ('ridge', Ridge(random_state=0))]

stack = StackingTransformer(estimators, regression=True, verbose=2)

stack = stack.fit(X_train, y_train)

S_train = stack.transform(X_train)
S_test = stack.transform(X_test)

# 使用stack特征作为第二层模型的输入数据