最短路问题--Floyd 畅通工程续

畅通工程续

某省自从实行了很多年的畅通工程计划后，终于修建了很多路。不过路多了也不好，每次要从一个城镇到另一个城镇时，都有许多种道路方案可以选择，而某些方案要比另一些方案行走的距离要短很多。这让行人很困扰。

现在，已知起点和终点，请你计算出要从起点到终点，最短需要行走多少距离。

Input

本题目包含多组数据，请处理到文件结束。

每组数据第一行包含两个正整数$N$和$M$$(0<N<200,0<M<1000)$，分别代表现有城镇的数目和已修建的道路的数目。城镇分别以$0$～$N$-$1$编号。

接下来是M行道路信息。每一行有三个整数$A$,$B$,$X$$(0<=A,B<N,A!=B,0<X<10000)$,表示城镇A和城镇B之间有一条长度为$X$的双向道路。

再接下一行有两个整数$S$,$T$$(0<=S,T<N)$，分别代表起点和终点。

Output

对于每组数据，请在一行里输出最短需要行走的距离。如果不存在从$S$到$T$的路线，就输出-1.

Floyd：

动态转移方程 $dist[i][j] = min(dist[i][j],dist[i][k] + dist[k][j])$;

初始化//$dist[i][j]$ 表示从i到j之间的最短距离 

 //dist[i][j] 表示从i到j之间的最短距离
 int dist[maxn][maxn];
 for (int i = ; i< n ;i++)
     for (int j =  ;j< n ;j++)
         dist[i][j] = edge[i][j];

时间复杂度 节点个数 $N$，边个数 $M$ $O$($N^3$)

• 求所有节点到节点 $1$ 的最短距离

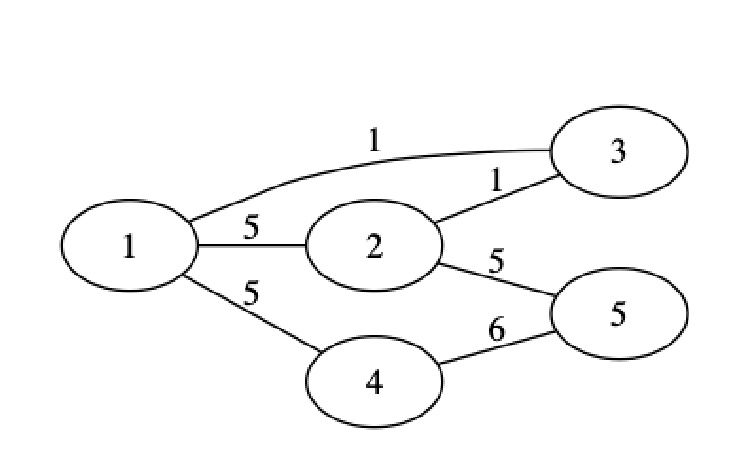
1. 初始化
• $dist$ 矩阵 – $dist[i][j]$ 表示节点 $i$ 到节点 $j$ 之间的最短路径长度 – $dist$ 初始化为 $edge$

2. 流程
(a) $step$ 1 • 通过节点 1 作为中转节点更新$dist$ • 更新公式 $dist[i][j]$ = $min(dist[i][1] + dist[1][j],dist[i][j])$;

(b) $step$ 2 • 通过节点 2 作为中转节点更新 $dist$ • 更新公式 $dist[i][j]$ = $min(dist[i][2] + dist[2][j],dist[i][j])$;

(c) $step$ 3 • 通过节点 3 作为中转节点更新 $dist$ • 更新公式 $dist[i][j]$ = $min(dist[i][3] + dist[3][j],dist[i][j])$;

(d) $step$ 4 • 通过节点 4 作为中转节点更新 $dist$ • 更新公式 $dist[i][j]$ = $min(dist[i][4] + dist[4][j],dist[i][j])$;

(e) $step$ 5 • 通过节点 5 作为中转节点更新 $dist$ • 更新公式 $dist[i][j]$ = $min(dist[i][5] + dist[5][j],dist[i][j])$;

有一说一，这道题显然代码为：

 #include <iostream>
 #include <cstdio>
 #include <cmath>
 #include <cstring>
 #include <algorithm>
 using namespace std;
 int const maxn=;
 int const INF=1e9;
 int dist[maxn][maxn];
 int n,m;
 int floyd(int s,int t){
  for(int t = ;t < n;t++)
      for(int i = ;i < n;i++)
          for(int j = ;j < n;j++)
          if(dist[i][j] > dist[i][t] + dist[t][j])
              dist[i][j] = dist[i][t] + dist[t][j];
  if(dist[s][t] == INF)
      return -;
  else
      return dist[s][t];
 }
 int main(){
     int a,b,x,s,t,ans;
     while(scanf("%d %d",&n,&m) != EOF)    {
         for(int i = ;i < n;i++)
         for(int j = ;j < n;j++)
             dist[i][j] = (i == j ?  : INF);
         while(m--)
         {
             scanf("%d %d %d",&a,&b,&x);
             if(x < dist[a][b])
                 dist[a][b] = dist[b][a] = x;
             }
             scanf("%d %d",&s,&t);
             ans = floyd(s,t);
             printf("%d\n",ans);
             }
     return ;
 }