CF1292C Xenon's Attack on the Gangs

题目链接:https://codeforces.com/problemset/problem/1292/C

题意

在一颗有n个节点的树上，给每个边赋值，所有的值都在\([0,n-2]\)内并且不重复，也就是一条边一个权值，令\(mex(u,v)\)表示从\(u到v\)这条简单路径上没有出现过的最小自然数，要求使所有路径的\(mex\)之和最大。

分析

最开始我一看这个题，统计答案的时候好像就需要\(O(N^2)\),那这个题好像统计个答案就可能会T？当我看见时限是\(3s\)的时候我就知道我想多了，分析时间复杂度的时候提前看一下时限，防止因看错时限分析错时间复杂度。

首先这个边的权值肯定有规律，不然枚举权值时间复杂度会很高，最开始我想的是从每个边开始\(dfs\)一下把经过次数最多的边设成0，然后依次类推，每次\(dfs\)不访问重复经过的点，发现存在一个什么问题呢，就是从不同的点开始\(dfs\)造成的结果不一样，所以这样不可行，不妨先画一条链来看看。



如果已经放好了\(0~x-1\)，考虑\(x\)放哪个位置，如果我把\(x\)放到\(5-v\)上，那么\(mex(u,5)\)就会是\(x\)，然后只有\(mex(u,v)\)会等于\(x+1\)，但要是把\(x\)放到\(u-1\)或\(4-5\)上，\(mex\)等于\(x+1\)的就不会只是\(mex(u,v)\)了。链上是这样，树上当然也是，所以\(x\)放到链的两端会使结果更优。



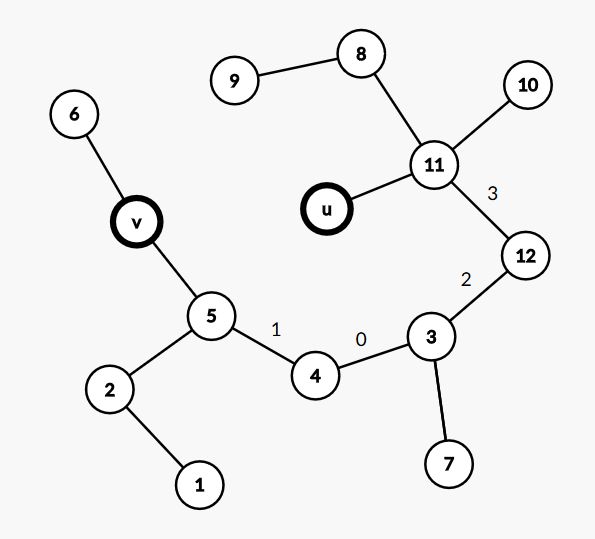
也就是这样，对于\(u-v\)的路径，4和5放在最两端时结果会更优，然后对最大值5的位置进行分类讨论，就可以求解出答案。

还有一个问题，如果我真的去把每个\(mex\)相加，的确很不现实，根据之前做过的一些类似的题，直接加上\(x\)相当于在\(0~x-1\)各加1，转化成对答案的贡献，也就是\(size_u*size_v\),这样求解起来就会相对简单。

之前已经讲过，从不同的点开始\(dfs\)的结果是不同的，所以不能像平常那样统计\(size\),而是应该在加一维表示根，这样才能保证得到我们想要的\(size\)，因为要枚举最大权值所在的地方，所以还要记录每个节点的父亲，同样也要记录根。

不妨用\(dp_{u,v}\)表示把\(0~x-1\)放到\(u-v\)的最大答案，\(s_{u,v}\)表示\(v\)以\(u\)为根时的子树大小，\(fa_{u,v}\)表示\(v\)以\(u\)为根时的父亲。于是有

\[dp_{u,v}=max(dp_{fa_{u,v},u},dp_{fa_{v,u},v})+s_{u,v}*s_{v,u}
然后此题就能得解，注意开long long
```
#include<iostream>
#define ll long long
using namespace std;
const int N=3e3+10;
struct Edge{
int to,nxt;
}e[N<<1];
int Head[N],len;
void Ins(int a,int b){
e[++len].to=b;e[len].nxt=Head[a];Head[a]=len;
}
int rt;ll s[N][N],dp[N][N],f[N][N];
void dfs(int u){
s[rt][u]=1;
for(int i=Head[u];i;i=e[i].nxt){
int v=e[i].to;
if(v==f[rt][u])continue;
f[rt][v]=u;
dfs(v);
s[rt][u]+=s[rt][v];
}
}
ll calc(int u,int v){
if(u==v)return 0;
if(dp[u][v])return dp[u][v];
return (dp[u][v]=max(calc(f[u][v],u),calc(f[v][u],v))+s[u][v]*s[v][u]);
}
int main(){
int n;
cin>>n;
for(int i=1;i<n;i++){
int a,b;
cin>>a>>b;
Ins(a,b);Ins(b,a);
}
for(int i=1;i<=n;i++)rt=i,dfs(i);
ll ans=0;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
ans=max(ans,calc(i,j));
cout<<ans;
}
```\]