机器学习理论基础学习3.2--- Linear classification 线性分类之线性判别分析(LDA)

　　在学习LDA之前，有必要将其自然语言处理领域的LDA区别开来，在自然语言处理领域， LDA是隐含狄利克雷分布（Latent Dirichlet Allocation，简称LDA），是一种处理文档的主题模型。本文只讨论线性判别分析，因此后面所有的LDA均指线性判别分析。

线性判别分析 LDA: linear discriminant analysis

一、LDA思想：类间小，类间大 （‘高内聚，松耦合’）

LDA是一种监督学习的降维技术，也就是说它的数据集的每个样本是有类别输出的，这点和PCA不同。PCA是不考虑样本类别输出的无监督降维技术。LDA的思想可以用一句话概括，就是“投影后类内方差最小，类间方差最大”，如下图所示。 我们要将数据在低维度上进行投影，投影后希望每一种类别数据的投影点尽可能的接近，而不同类别的数据的类别中心之间的距离尽可能的大。

可能还是有点抽象，先看看最简单的情况。

假设有两类数据，分别为红色和蓝色，如下图所示，这些数据特征是二维的，希望将这些数据投影到一维的一条直线，让每一种类别数据的投影点尽可能的接近，而红色和蓝色数据中心之间的距离尽可能的大。

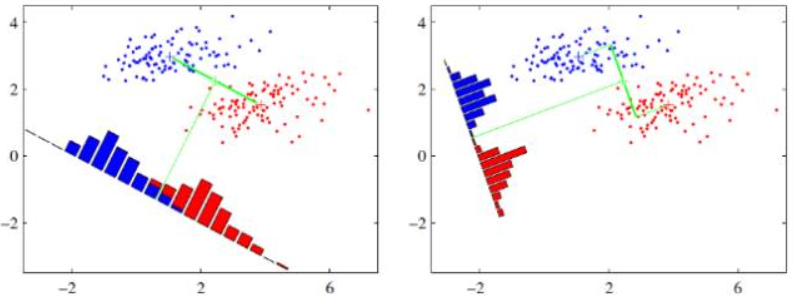
　　上图中提供了两种投影方式，哪一种能更好的满足我们的标准呢？从直观上可以看出，右图要比左图的投影效果好，因为右图的黑色数据和蓝色数据各个较为集中，且类别之间的距离明显。左图则在边界处数据混杂。以上就是LDA的主要思想了，当然在实际应用中，数据是多个类别的，我们的原始数据一般也是超过二维的，投影后的也一般不是直线，而是一个低维的超平面。

二、LDA原理与流程

 

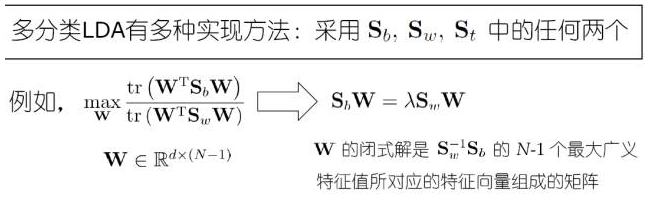
三、LDA分类

四、LDA降维 

五、LDA与PCA的相同点和不同点

LDA用于降维，和PCA有很多相同，也有很多不同的地方

相同点

• 1）两者均可以对数据进行降维。
• 2）两者在降维时均使用了矩阵特征分解的思想。
• 3）两者都假设数据符合高斯分布。

不同点

• 1）LDA是有监督的降维方法，而PCA是无监督的降维方法
• 2）LDA降维最多降到类别数k-1的维数，而PCA没有这个限制。
• 3）LDA除了可以用于降维，还可以用于分类。
• 4）LDA选择分类性能最好的投影方向，而PCA选择样本点投影具有最大方差的方向。这点可以从下图形象的看出，在某些数据分布下LDA比PCA降维较优。

                                       

四、LDA的优缺点

　　LDA算法既可以用来降维，又可以用来分类，但是目前来说，主要还是用于降维。在进行图像识别相关的数据分析时，LDA是一个有力的工具。下面总结下LDA算法的优缺点。

优点

• 1）在降维过程中可以使用类别的先验知识经验，而像PCA这样的无监督学习则无法使用类别先验知识。
• 2）LDA在样本分类信息依赖均值而不是方差的时候，比PCA之类的算法较优。

缺点

• 1）LDA不适合对非高斯分布样本进行降维，PCA也有这个问题。
• 2）LDA降维最多降到类别数k-1的维数，如果我们降维的维度大于k-1，则不能使用LDA。当然目前有一些LDA的进化版算法可以绕过这个问题。
• 3）LDA在样本分类信息依赖方差而不是均值的时候，降维效果不好。
• 4）LDA可能过度拟合数据。

参考文献：

【1】机器学习(30)之线性判别分析(LDA)原理详解

【2】详细解说LDA线性判别分析方法