DRTREE - Dynamically-Rooted Tree 题解

DRTREE - Dynamically-Rooted Tree

本题建议评蓝。

思路：

题目就是要对一颗不定根树求子树权值和。

这题不带修，如果带修难度会增加一点，就跟 遥远的国度 差不多。

首先分析一下在以不同根下子树的变化。

当一颗树以 1 号节点为根时，比如说长这样：

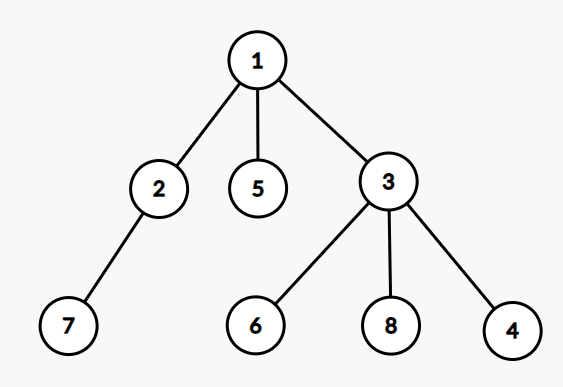
假设每个点的权值为 1，那么这 8 个点的子树权值和（在这里也是子树大小）分别为：8，2，4，1，1，1，1，1。这是可以通过预处理得到的。

而当整个树的根变化后，我们分情况讨论：（假设变化后的根为 \(A\)，要求的点为 \(B\)）

• 当 \(A=B\) 时，毫无疑问答案是整个树的权值和。

• 当 \(A\) 不在 \(B\) 的子树中时，我们发现，\(B\) 的子树不会发生变化，那么子树权值和也就是在以 1 为根的情况下的权值和。

• 当 \(A\) 在 \(B\) 的子树中时，情况复杂起来了。举个例子，比如说在上图中，将根换成 8 号节点，求 3 号节点：

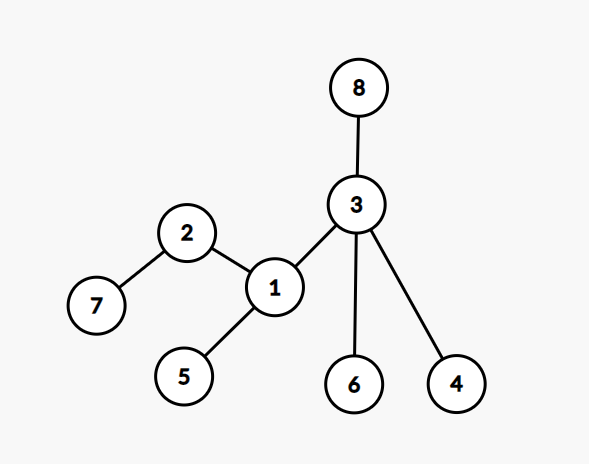
我们可以发现，这时的 3 号节点的子树权值和变成了：树的权值总和减去 3 号点在 8 号点方向的子树的权值和。（这个例子可能不太好，可以自己画几个图模拟一下。）

因此我们可以得出结论：在这种情况下，答案就是树的权值和减去 \(B\) 在 \(A\) 方向上的子树的权值和。

还剩下几个问题：

怎么判断一个点 \(A\) 是不是在另一个点 \(B\) 的子树中？

方法很多，有的简单有的相对麻烦。

比如说求 \(A\)，\(B\) 的 \(\text{LCA}\) ，看看是不是 \(B\)，时间复杂度为 \(O(\log n)\)。

再比如说用树剖加线段树，将 \(B\) 的“权值”设为 \(1\) ，其他的点设为 \(0\)，判断从点

\(A\) 到 \(1\) 的路径上的“权值”最大值是不是 \(1\)，时间复杂度为 \(O(\log ^2n)\)。

这里我们使用了最简单也是最快的方法，利用 \(\text{dfs}\) 序进行判断。

（我们用 \(\text{dfn}\) 表示 \(\text{dfs}\) 序，\(\text{size}\) 表示子树大小。）

因为当且仅当 \(\text{dfn}[B]\le \text{dfn}[A] \le \text{dfn}[B]+\text{size}[B]-1\) 时，点 \(A\) 会在 \(B\) 的子树中，故可以通过这个式子进行判断，时间复杂度为 \(O(1)\)。

怎么求一个点 \(A\) 在 另一个点 \(B\) 的方向上的子树权值和？（点 \(B\) 在 \(A\) 的子树内）

因为我们预处理了子树权值和，所以我们只需要求出点 \(A\) 在点 \(B\) 方向上的儿子就可以了。

我们可以用树剖解决这个问题（当然，倍增也可以，但更慢。）：

我们按链一段段跳，如果跳的途中发现某点所在的链顶的父亲是另一个点，那么返回链顶。如果一直跳到了最后，因为此时两点在同一条链上，所以这时返回深度较小的点的重儿子就行了。

int lcason(int x,int y){
    while(top[x]!=top[y]){
        if(dep[top[x]]<dep[top[y]]) Swap(x,y);
        if(fa[top[x]]==y) return top[x];
        x=fa[top[x]];
    }
    if(dep[x]>dep[y]) Swap(x,y);
    return son[x];
}

注意事项：

加边方式比较奇怪，注意一下。

点权较大，记得开 long long 。

代码：

#include <bits/stdc++.h>
using namespace std;
const int N=200100;
typedef long long ll;

int to[N],nxt[N],head[N],w[N];//链星
int dfn[N],siz[N],top[N],dep[N],son[N],fa[N],rnk[N];//树剖
int idx,n,q,in1,cnt,rt=1;
ll W[N],sum,ans;//W表示子树权值和
char op[2];

void add(int u,int v){idx++;to[idx]=v;nxt[idx]=head[u];head[u]=idx;}
void Swap(int &x,int &y){int t=x;x=y;y=t;}

void dfs_1(int s,int gr){
    siz[s]=1;son[s]=-1;fa[s]=gr;
    dep[s]=dep[gr]+1;
    W[s]=w[s];sum+=w[s];//预处理子树权值和
    for(int i=head[s];i;i=nxt[i]){
        int v=to[i];
        if(v==gr) continue;
        dfs_1(v,s);
        siz[s]+=siz[v];W[s]+=W[v];
        if(son[s]==-1||siz[v]>siz[son[s]]) son[s]=v;
    }
}

void dfs_2(int s,int tp){
    top[s]=tp;dfn[s]=++cnt;rnk[cnt]=s;
    if(son[s]==-1) return ;
    dfs_2(son[s],tp);
    for(int i=head[s];i;i=nxt[i]){
        int v=to[i];
        if(v==fa[s]||v==son[s]) continue;
        dfs_2(v,v);
    }
}

int lcason(int x,int y){//求某点在另一个点方向上的儿子
    while(top[x]!=top[y]){
        if(dep[top[x]]<dep[top[y]]) Swap(x,y);
        if(fa[top[x]]==y) return top[x];
        x=fa[top[x]];
    }
    if(dep[x]>dep[y]) Swap(x,y);
    return son[x];
}

int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        scanf("%d",&w[i]);
    for(int i=1;i<n;i++){
        scanf("%d",&in1);
        add(in1,i+1);add(i+1,in1);//加边
    }
    dfs_1(1,0);dfs_2(1,1);//先以1为根跑树剖
    scanf("%d",&q);
    while(q--){
        scanf("%s%d",op+1,&in1);
        if(op[1]=='S'){
            if(rt==in1) ans=sum;
            else if(dfn[in1]<=dfn[rt]&&dfn[rt]<=dfn[in1]+siz[in1]-1) ans=sum-W[lcason(in1,rt)];
            else ans=W[in1];//我们讨论过的三种情况
            cout<<ans<<'\n';
        }
        if(op[1]=='R') rt=in1;
    }
    return 0;
}

其他：

类似的题目：

P3979 遥远的国度,

Jamie and Tree（这两个都带修）。