FHQ-Treap的详细图解

第一部分 按值分裂的 FHQ-Treap

按值分裂的 FHQ-Treap 的典型例题是P3369 【模板】普通平衡树。

思路

FHQ-Treap 是什么？

FHQ-Treap 是二叉搜索树的一种。

比如：

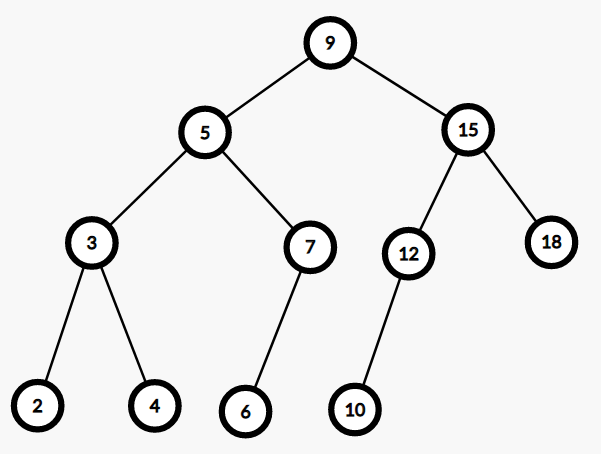
FHQ-Treap 的思想是什么？

分裂->操作->合并

下面我们就来慢慢讲这些操作。

分裂

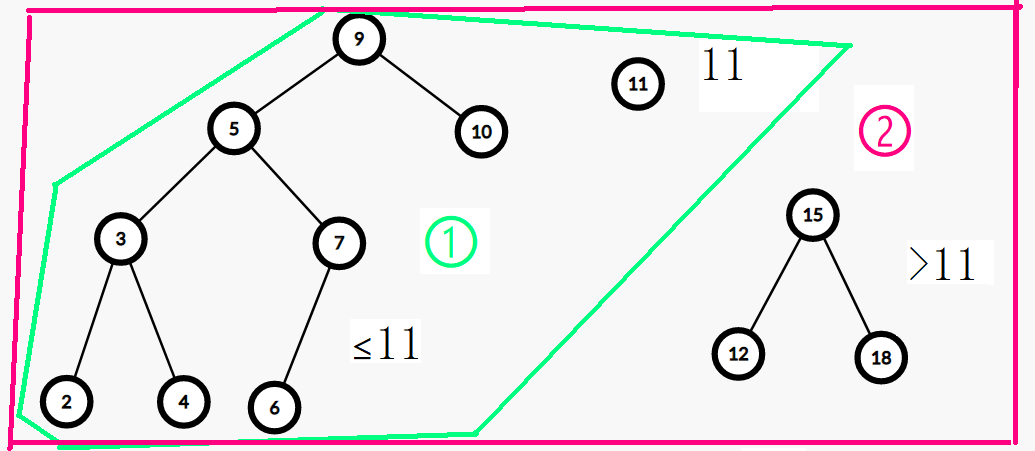
我们可以根据给定的 \(k\) 将平衡树分成两个部分，一部分节点的值都小于等于 \(k\)，一部分节点的值都大于 \(k\)。

比如 \(k = 10\) 时我们把上图分成这样两个部分：

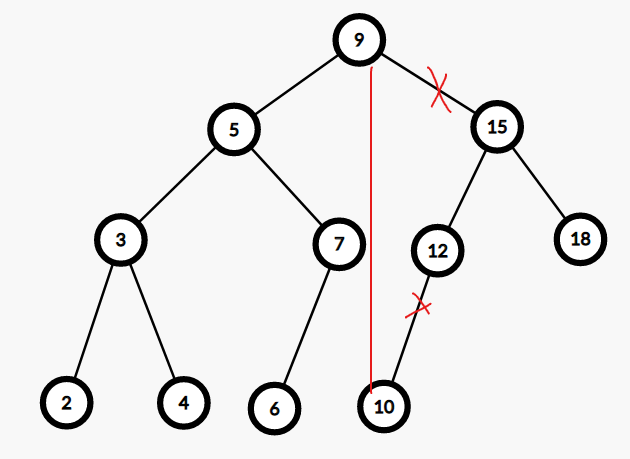
即：

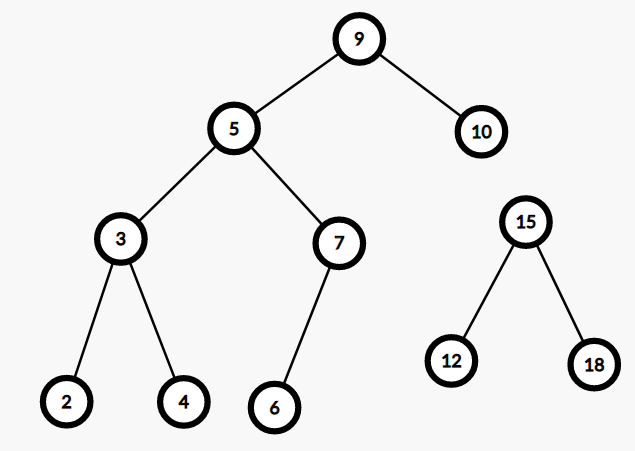
左边的 \(2, 3, 4, 5, 6, 7, 9, 10\) 都小于等于 \(10\)，右边的 \(12, 15, 18\) 都大于 \(10\)。

那么，怎么让计算机实现呢？

我们发现图中的 \(9, 10\) 本不相连，但在分裂后却是相连的，所以我们并不能讨论是否只断掉某条边就可以实现分裂。

分裂的过程实际上是在找这个点的过程中完成的：

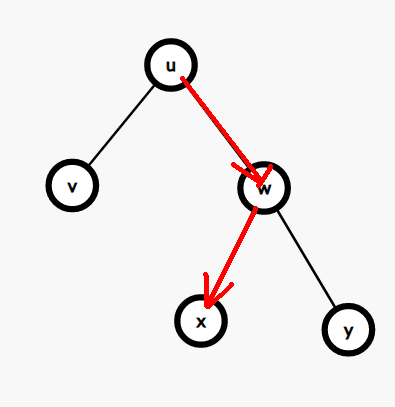
下面我们以分裂出 \(\leq k\) 这部分为例讲讲怎么实现分裂。

首先我们发现，当遍历到一个节点 \(u\)，如果 \(u\) 的值小于等于 \(k\)，我们容易根据二叉搜索树的性质得出结论：\(u\) 所有的左子树的值 \(\leq k\)：

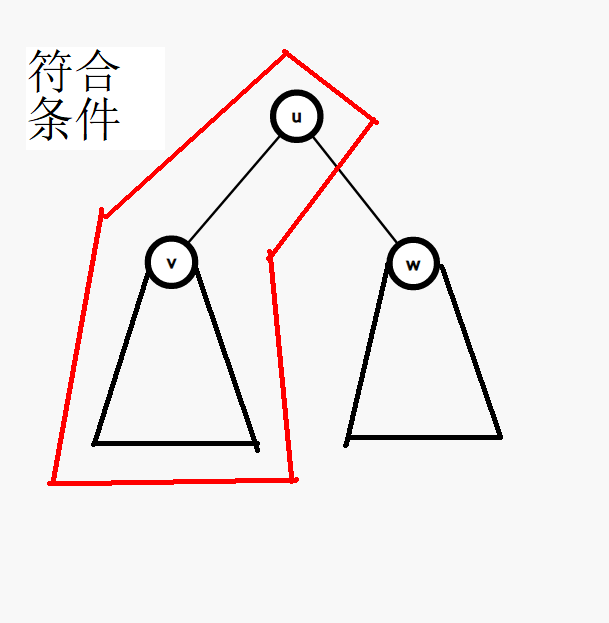
\(u\) 的右子树的值都不小于 \(u\) 的值，也有可能有 \(\leq k\) 的部分，我们也要把它们（当然也有可能是）连起来。

因为 \(u\) 的右子树任何一个数值都比 \(u\) 的数值要大，所以从 \(u\) 连向任何右边的点都是合法的：

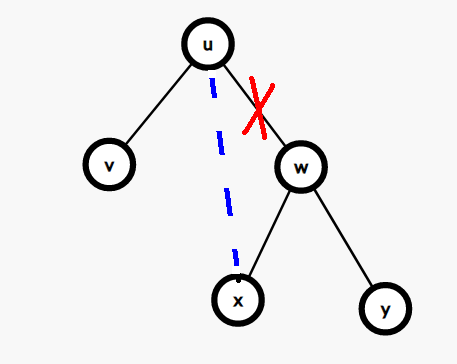
所以当我们在遍历右子树的某个点 \(d\) 的时候，如果又出现了 \(d\) 的值 \(\leq k\)，那么就可以把 \(u\) 的连接右子树的边连到 \(d\) 上：

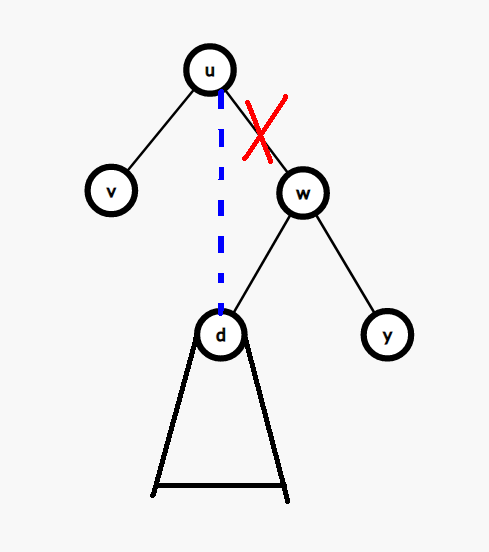
还有一个比较特殊的点，它没有父节点，那么它就作为根。

---

以上是处理 \(\leq k\) 的部分的思想，处理 \(> k\) 的方法类似，反着来就行了。

合并

FHQ-Treap 和 普通 Treap 一样，也分优先级，维护一个堆的性质。

采用上小下大或上大下小都可以。

合并比分裂容易得多，谁的优先级高，谁就先上。

插入

分裂：假如要插入 \(k\)，将平衡树拆分成 \(\leq k\) 和 \(>k\) 两部分；

新建节点：再新建一个节点，值为 \(k\)；

合并：先合并 \(\leq k\) 的部分和新建节点，然后再与 \(>k\) 的部分合并。

删除

分裂：假如要删除 \(k\)，将平衡树分成 \(<k, =k, >k\) 三个部分。

合并：最后将 \(=k\) 的那个部分的左右子树合并，再把这三个部分合并就可以了。

查询一个数的排名

分裂：将平衡树分裂成 \(\leq (k - 1)\) 和 \(>(k - 1)\) 的两个部分。

结果：排名就是 \(\leq (k - 1)\) 这一子树的大小 \(+1\)。

合并：将分裂出来的两个部分合并。

使用排名来查找数字

设当前遍历到点 \(u\)。

1. 如果 \(u\) 的左子树的大小 \(+1\) 等于排名，那么结果就是 \(u\) 这个节点的数字；
2. 如果 \(u\) 的左子树大小大于等于排名，说明结果在左子树中，那么递归查询左子树；
3. 否则遍历 \(u\) 的右子树，注意，查询右子树时记得将排名减去 \((左子树的大小 + 1)\)。

找 \(x\) 的前驱

分裂：将平衡树分成 \(\leq (x - 1)\) 和 \(>(x - 1)\) 的两个部分

结果：使用上面的“使用排名来查找数字”的方法求出 \(\leq (x - 1)\) 部分的平衡树的最大的一个数。

合并：将分裂出来的两个部分合并。

找 \(x\) 的后继

分裂：将平衡树分成 \(\leq x\) 和 \(>x\) 的两个部分

结果：使用上面的“使用排名来查找数字”的方法求出 \(>x\) 部分的平衡树的最小的一个数。

合并：将分裂出来的两个部分合并。

例题代码

#include <bits/stdc++.h>

using namespace std;

const int N = 100010;

struct node {
	int l, r;
	int size;
	int rnd;
	int key;
} tr[N];

int root, idx;

void pushup(int u) {
	tr[u].size = tr[tr[u].l].size + tr[tr[u].r].size + 1;
}

int newnode(int key) {
	idx++;
	tr[idx].key = key;
	tr[idx].rnd = rand();
	tr[idx].size = 1;
	tr[idx].l = tr[idx].r = 0;
	return idx;
}

void split(int u, int key, int &x, int &y) {
	if (!u) {
		x = y = 0;
		return;
	}
	if (tr[u].key <= key) {
		x = u;
		split(tr[u].r, key, tr[u].r, y);
	}
	else {
		y = u;
		split(tr[u].l, key, x, tr[u].l);
	}
	pushup(u);
}

int merge(int x, int y) {
	if ((!x) || (!y)) return x | y;
	if (tr[x].rnd < tr[y].rnd) {
		tr[x].r = merge(tr[x].r, y);
		pushup(x);
		return x;
	}
	else {
		tr[y].l = merge(x, tr[y].l);
		pushup(y);
		return y;
	}
}

void insert(int key) {
	int x, y, z;
	split(root, key, x, y);
	z = newnode(key);
	root = merge(merge(x, z), y);
}

void del(int key) {
	int x, y, z;
	split(root, key, x, y);
	split(x, key - 1, x, z);
	z = merge(tr[z].l, tr[z].r);
	root = merge(merge(x, z), y);
}

int get_rank_by_key(int key) {
	int x, y, z;
	split(root, key - 1, x, y);
	int ans = tr[x].size + 1;
	root = merge(x, y);
	return ans;
}

int get_key_by_rank(int u, int rk) {
	if (tr[tr[u].l].size + 1 == rk) return tr[u].key;
	else if (tr[tr[u].l].size >= rk) return get_key_by_rank(tr[u].l, rk);
	else return get_key_by_rank(tr[u].r, rk - tr[tr[u].l].size - 1);
}

int get_pre(int key) {
	int x, y, z;
	split(root, key - 1, x, y);
	int ans = get_key_by_rank(x, tr[x].size);
	root = merge(x, y);
	return ans;
}

int get_nxt(int key) {
	int x, y, z;
	split(root, key, x, y);
	int ans = get_key_by_rank(y, 1);
	root = merge(x, y);
	return ans;
}

int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);

	int T;
	cin >> T;
	int opt, x;
	while (T--) {
		cin >> opt >> x;
		if (opt == 1) insert(x);
		else if (opt == 2) del(x);
		else if (opt == 3) cout << get_rank_by_key(x) << '\n';
		else if (opt == 4) cout << get_key_by_rank(root, x) << '\n';
		else if (opt == 5) cout << get_pre(x) << '\n';
		else cout << get_nxt(x) << '\n';
	}
	return 0;
}

第二部分 按大小（\(size\)）分裂的 FHQ-Treap

按大小分裂的 FHQ-Treap 的典型例题是P3391 【模板】文艺平衡树。

思路

在所有操作中，除了分裂操作以外，都是一样的。

只有分裂操作与按值分裂的不同，比较的对象是大小：

原图：

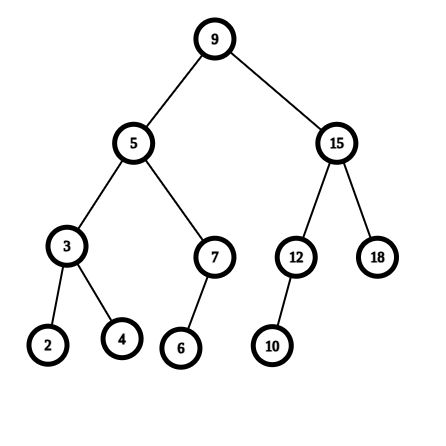
操作：

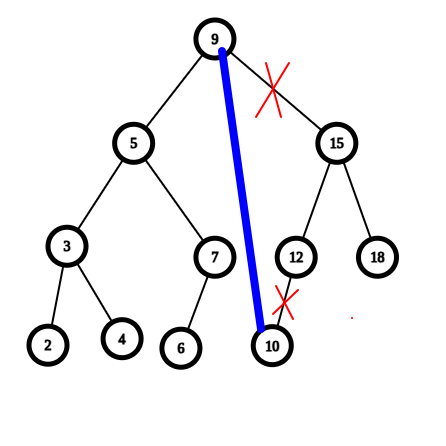
结果：

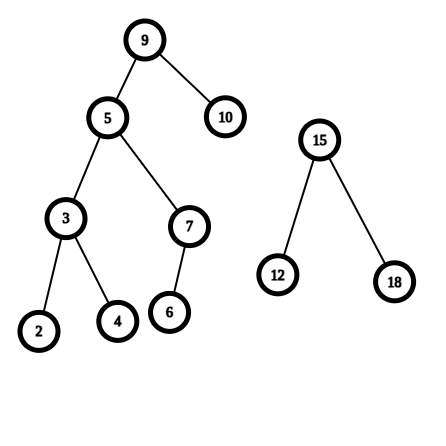
例题代码

#include <bits/stdc++.h>

using namespace std;

const int N = 100010;

struct node {
    int l, r;
    int sz;
    int key;
    int rnd;
    int tag;
} tr[N];

int root, idx;

void pushup(int u) {
    tr[u].sz = tr[tr[u].l].sz + tr[tr[u].r].sz + 1;
}

int newnode(int key) {
    idx++;
    tr[idx].key = key;
    tr[idx].rnd = rand();
    tr[idx].tag = 0;
    tr[idx].l = tr[idx].r = 0;
    tr[idx].sz = 1;
    return idx;
}

void pushdown(int u) {
    if (tr[u].tag) {
        tr[tr[u].l].tag ^= 1;
        tr[tr[u].r].tag ^= 1;
        swap(tr[u].l, tr[u].r);
        tr[u].tag = 0;
    }
}

void split(int u, int sz, int &x, int &y) {
    if (!u) {
        x = y = 0;
        return;
    }
    pushdown(u);
    if (tr[tr[u].l].sz + 1 <= sz) {
        x = u;
        split(tr[u].r, sz - tr[tr[u].l].sz - 1, tr[u].r, y);
    }
    else {
        y = u;
        split(tr[u].l, sz, x, tr[u].l);
    }
    pushup(u);
}

int merge(int x, int y) {
    if ((!x) || (!y)) return x | y;
    if (tr[x].rnd > tr[y].rnd) {
        pushdown(x);
        tr[x].r = merge(tr[x].r, y);
        pushup(x);
        return x;
    }
    else {
        pushdown(y);
        tr[y].l = merge(x, tr[y].l);
        pushup(y);
        return y;
    }
}

void insert(int p, int key) {
    int x, y, z;
    split(root, p - 1, x, y);
    z = newnode(key);
    root = merge(merge(x, z), y);
}

void reverse_arr(int l, int r) {
    int x, y, z;
    split(root, r, x, z);
    split(x, l - 1, x, y);
    tr[y].tag ^= 1;
    root = merge(merge(x, y), z);
}

void dfs(int u) {
    if (!u) return;
    pushdown(u);
    dfs(tr[u].l);
    cout << tr[u].key << ' ';
    dfs(tr[u].r);
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int n, T;
    cin >> n >> T;
    for (int i = 1; i <= n; i++) insert(i, i);
    while (T--) {
        int l, r;
        cin >> l >> r;
        reverse_arr(l, r);
    }

    dfs(root);

    return 0;
}

第三部分 练习

P4008 [NOI2003] 文本编辑器

题目描述

思路

文艺平衡树的基本运用。

代码

#include <bits/stdc++.h>

using namespace std;

const int N = 3200000;

struct node {
    int l, r;
    int size;
    char key;
    int rnd;
} tr[N];

int root, idx;

int newnode(char key) {
    idx++;
    tr[idx].key = key;
    tr[idx].rnd = rand();
    tr[idx].size = 1;
    tr[idx].l = tr[idx].r = 0;
    return idx;
}

void pushup(int u) {
    tr[u].size = tr[tr[u].l].size + tr[tr[u].r].size + 1;
}

void split(int u, int sz, int &x, int &y) {
    if (!u) {
        x = y = 0;
        return;
    }
    if (tr[tr[u].l].size + 1 <= sz) {
        x = u;
        split(tr[u].r, sz - tr[tr[u].l].size - 1, tr[u].r, y);
    }
    else {
        y = u;
        split(tr[u].l, sz, x, tr[u].l);
    }
    pushup(u);
}

int merge(int x, int y) {
    if ((!x) || (!y)) return x | y;
    if (tr[x].rnd < tr[y].rnd) {
        tr[x].r = merge(tr[x].r, y);
        pushup(x);
        return x;
    }
    else {
        tr[y].l = merge(x, tr[y].l);
        pushup(y);
        return y;
    }
}

int p;

void insert(int sz) {
    int x, y, z = 0, s;
    split(root, p, x, y);
    char ch = 0;
    for (int i = 1; i <= sz; i++) {
        ch = getchar();
        if (ch == '\n' || ch == '\r') {
            i--;
            continue;
        }
        s = newnode(ch);
        if (!z) z = s;
        else z = merge(z, s);
    }
    root = merge(merge(x, z), y);
}

void del(int sz) {
    int x, y, z;
    if (!p) {
        split(root, sz, x, y);
        root = y;
        return;
    }
    split(root, p + sz, x, z);
    split(x, p, x, y);
    root = merge(x, z);
}

void output(int u) {
    if (!u) return;
    output(tr[u].l);
    putchar(tr[u].key);
    output(tr[u].r);
}

void print(int sz) {
    int x, y, z;
    split(root, p + sz, x, z);
    split(x, p, x, y);
    output(y);
    root = merge(merge(x, y), z);
    putchar('\n');
}

int main() {
    int T;
    char opt[10];
    scanf("%d", &T);

    while (T--) {
        scanf("%s", opt);
        if (opt[0] == 'M') scanf("%d", &p);
        else if (opt[0] == 'I') {
            int sz;
            scanf("%d", &sz);
            insert(sz);
        }
        else if (opt[0] == 'D') {
            int sz;
            scanf("%d", &sz);
            del(sz);
        }
        else if (opt[0] == 'G') {
            int sz;
            scanf("%d", &sz);
            print(sz);
        }
        else if (opt[0] == 'P') p--;
        else p++;
        // output(root);
        // cout << endl;
    }
    return 0;
}

P2596 [ZJOI2006] 书架

题目描述

思路

对每一种操作，

对 FHQ-Treap 树按要求进行分裂，

再用不同的顺序进行合并，

就实现了题目中的各种调换。

是练习分裂的绝佳好题。

代码

#include <bits/stdc++.h>

using namespace std;

const int N = 90010;

struct node {
    int l, r;
    int size;
    int key;
    int rnd;
    int fa;
} tr[N];

int root, idx;
int st[N];

int newnode(int key, int fa) {
    idx++;
    st[key] = idx;
    tr[idx].key = key;
    tr[idx].fa = fa;
    tr[idx].rnd = rand();
    tr[idx].size = 1;
    tr[idx].l = tr[idx].r = 0;
    return idx;
}

void pushup(int u) {
    tr[u].size = tr[tr[u].l].size + tr[tr[u].r].size + 1;
    if (tr[u].l) tr[tr[u].l].fa = u;
    if (tr[u].r) tr[tr[u].r].fa = u;
}

void split(int u, int sz, int &x, int &y) {
    if (!u) {
        x = y = 0;
        return;
    }
    if (tr[tr[u].l].size + 1 <= sz) {
        x = u;
        split(tr[u].r, sz - tr[tr[u].l].size - 1, tr[u].r, y);
    }
    else {
        y = u;
        split(tr[u].l, sz, x, tr[u].l);
    }
    pushup(u);
}

int merge(int x, int y) {
    if ((!x) || (!y)) return x | y;
    if (tr[x].rnd < tr[y].rnd) {
        tr[x].r = merge(tr[x].r, y);
        pushup(x);
        return x;
    }
    else {
        tr[y].l = merge(x, tr[y].l);
        pushup(y);
        return y;
    }
}

int get_rank(int ver, int rt) {
    int rk = tr[tr[ver].l].size;
    while (ver != rt) {
        int fa = tr[ver].fa;
        if (tr[fa].r == ver) rk += tr[tr[fa].l].size + 1;
        ver = fa;
    }
    return rk + 1;
}

void insert(int p, int key) {
    int x, y, z;
    split(root, p - 1, x, y);
    z = newnode(key, 0);
    root = merge(merge(x, z), y);
}

void top(int s) {
    int p = get_rank(st[s], root);
    int x, y, z;
    split(root, p, x, z);
    split(x, p - 1, x, y);
    root = merge(merge(y, x), z);
}

void bottom(int s) {
    int p = get_rank(st[s], root);
    int x, y, z;
    split(root, p, x, z);
    split(x, p - 1, x, y);
    root = merge(merge(x, z), y);
}

void change(int s, int t) {
    if (!t) return;
    int p = get_rank(st[s], root);
    int x, y, z, l, r;
    if (t > 0) {
        split(root, p + 1, x, l);
        split(x, p, x, z);
        split(x, p - 1, x, y);
    }
    else {
        split(root, p, x, l);
        split(x, p - 1, x, z);
        split(x, p - 2, x, y);
    }
    root = merge(x, merge(z, merge(y, l)));
}

int ask(int p) {
    return get_rank(st[p], root);
}

int query(int p) {
    int x, y, z;
    split(root, p, x, z);
    split(x, p - 1, x, y);
    int ans = tr[y].key;
    root = merge(merge(x, y), z);
    return ans;
}

int n, m;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        int x;
        cin >> x;
        insert(i, x);
    }

    char opt[10];
    int t1, t2;
    while (m--) {
        cin >> opt;
        if (opt[0] == 'T') {
            cin >> t1;
            top(t1);
        }
        else if (opt[0] == 'B') {
            cin >> t1;
            bottom(t1);
        }
        else if (opt[0] == 'I') {
            cin >> t1 >> t2;
            change(t1, t2);
        }
        else if (opt[0] == 'A') {
            cin >> t1;
            cout << ask(t1) - 1 << '\n';
        }
        else if (opt[0] == 'Q') {
            cin >> t1;
            cout << query(t1) << '\n';
        }
    }
    return 0;
}