A/B实验背后的秘密：样本量计算

更多技术交流、求职机会，欢迎关注字节跳动数据平台微信公众号，回复【1】进入官方交流群

一、前言

• 背景：

AB实验具有一定前瞻性，统计性，科学性的特性。用好了就实现了在大数据时代的充分利用数据分析问题，解决问题，为决策提供强有力的依据，但是有时候用户在使用AB实验时候，会出现一些痛点和疑惑。

• 痛点：

  每次实验需要多少流量

  实验时间开多长没有概念

• 解决问题：

  为了验证某一个功能特性，一个实验需要开多少流量。

  一个实验需要开多长时间

二、统计基础概念

1、研究对象

总体X：研究问题某个数量指标。

2、入手点

个体：总体中的一个元素 xi

样本：一部分个体 Xi

3、统计量（工具）

常见统计量：

（1）样本均值

反映出总体X数学期望。

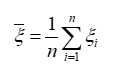
（2）样本方差

方差 是各数据偏离平均值 差值的平方和 的平均数。反映的是总体X方差。

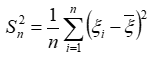
样本修正

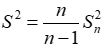
得出

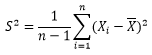
（3）样本均方差

均方差就是标准差，标准差就是均方差。

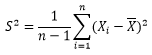
对上面公式开平方。

（4）样本 K 阶矩

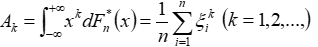
（5）样本 K 阶中心矩

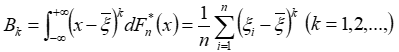
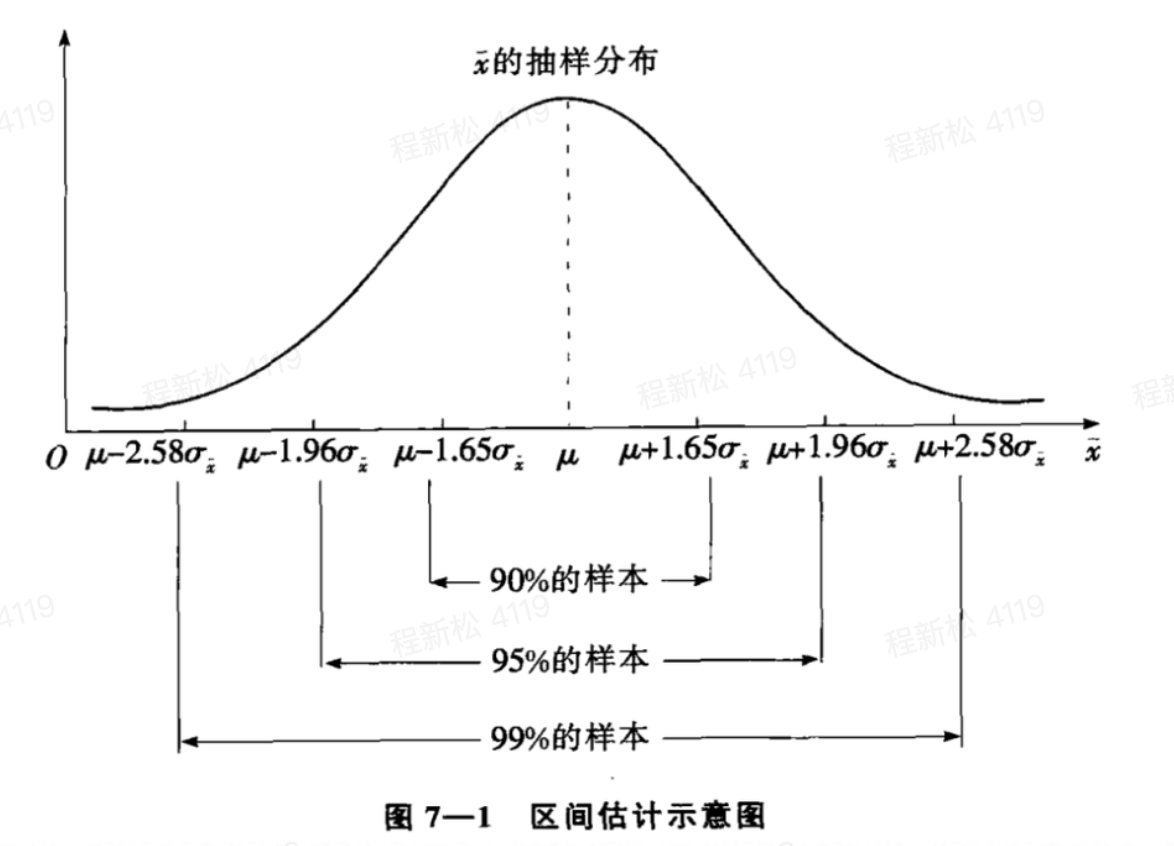
4、抽样分布

这里不做详细的叙述，后续推导中需要使用到以上概念，具体可以参考网上介绍。

• 标准正态分布N(0, 1)

• Ka方分布

• t-分布

• F-分布

5、抽样定理

简单介绍几个抽样定理

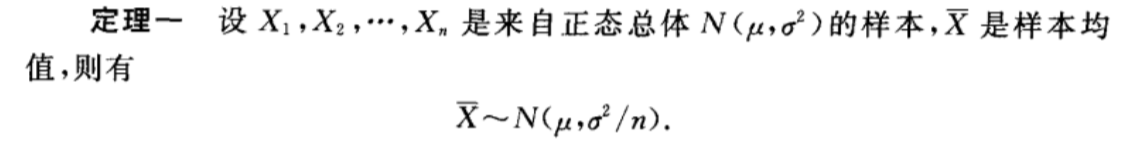
6、参数估计

通俗的说：样本参数去估计总体的参数。

举个：

• 样本均值估计总体均值，

• 用样本比例去估计总体比例，

• 用样本方差估计总体方差

（1）分类：点估计和区间估计

• 点估计通俗的说：用样本的统计量的值直接作为总体参数的估计值。

• 区间估计通俗的说：在点估计的基础上，给出总体参数估计的一个区间范围。

（2）置信区间和置信水平

通俗的说：区间估计中，样本统计量构造的总体参数的估计区间，称为置信区间。

举个：

• 100个样本，每一个样本构造一个置信区间，100个样本构造的总体参数的100个置信区间中，有95%的区间包含了总体参数的真值，5%则没有包含。

大样本下，样本均值的置信区间：

（3）总体均值的区间估计原理

大样本下，根据中心极限定理，可以得到的样本均值的抽样分布。

7、假设检验

我们来看一下一个简单的假设性检验的例子：

根据水稻长势，估计平均亩产310kg，收割时，抽取10块地，测平均亩产320kg，如水稻产量服从正态分布N(u, 144)，问所估计平均亩产是否正确？（a = 0.05，Z0.05 = 1.645，Z0.025 = 1.96）

分析：当方差已经的情况下，使用Z检验；未知的时候，使用t检验

三、一个简单并完整的AB实验例子

1、背景和设置

• 背景：有个web应用，接入火山引擎的AB测试客户端sdk，上报各种事件埋点。

• 确认优化的目标：注册流程改版，从而提供注册转换率。

• 注册流程的A/B测试：之前是使用了图片校验码的方式，但是注册转化率偏低。提出设想：图片校验码方式改成短信校验码方式，是因为降低了用户输入的难度从而可以提高注册转换率。

• 我们设置

  核心指标：注册转化率

  设置版本：1个对照版本（图片校验码）。1个实验版本（短信验证码）。

  设置版本流量：总流量我们设置50%，各个版本均匀分配。

• web应用引入我们客户端分流sdk的，然后将版本代码插入到项目中。

2、结果分析

分别为两个版本分配了25%的用户流量，通过2个自然周左右的实验观察，数据显示。

结果：新版本（短信校验码）的注册转化率提升了接近10%，并且95%置信区间是[8%, 12%]，

分析：说明这个实验版本推广到全量用户之后，95%的概率下至少会有8%到12%的提升。

决策：基于这个实验结果，产品经理选择将新版本注册流程推送给全部用户，显著提升了注册转化率。

四、详细介绍样本量计算

1、注册流程改版例子

实验运行后，用户开始进组。

1天后数据统计

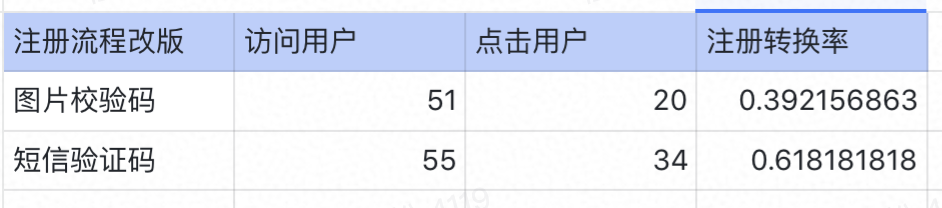
这就能说明：短信验证码的功能有效提高注册转换率？

2天后数据统计

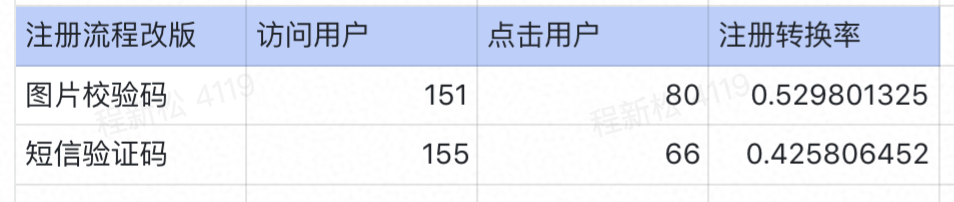
这就能说明：图片验证码的功能有效提高注册转换率？

那么到底，注册流程改版对于提高注册转换率是否有显著性提高呢？暂时是不能给出结论的，因为数据样本还不够大，不能充分说明。

理论上：样本量越多越好。

现实上：1、自身样本不够大；2、试错成本大。

选择样本数量是个技术活：样本量太小，实验不严谨；样本量太大，老板不高兴。

那么样本太小带来的问题是什么呢？样本太小导致没有统计学意义，而且会出现样本偏差情况，可能会造成“假阳性”的实验结论等问题。

那么样本太大带来的问题是什么呢？首先我们需要知道样本并不是总体，我们通过样本来替代样本太大会造成实验成本增加，以及产品本身的试错成本等。

那么问题来了：如何确定一个“最小”的样本数量，在保证实验“可靠性”的同时，不会浪费过多流量？

2、最小样本公式

统计学里有最小样本量计算的公式：

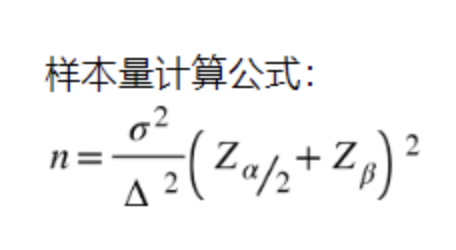
说明：

（1）n是每组所需样本量，因为A/B测试一般至少2组，所以实验所需样本量为2n；

（2）α和β分别称为第一类错误概率和第二类错误概率，一般分别取0.05和0.2；

（3）Z为正态分布的分位数函数；

（4）Δ为两组数值的差异，如注册转换率50%到60%，那么Δ就是10%；

（5）σ为标准差，是数值波动性的衡量，σ越大表示数值波动越厉害。

从而可知：实验两组数值差异Δ越大或者数值波动性σ越小，所需要的样本量就越小。

其中很多同学可能对于「第一类错误」和「第二类错误」不是很清楚。我们来简单解释一下：

（1）第一类错误：H0为真，拒绝H0。“本身没提升，但误判为有提升”

（2）第二类错误：H1为真，接受H0。“本身有提升，但没有察觉提升”

3、方法一：假设两个转换率方差相等

条件：假设两个转换率的方差（可变性）相等。

上面公式转换为：

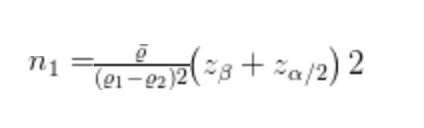
说明：

（1）e1和e2是真实的注册转换率。

（2）e 是合并方差估计量。

（3）α是显著性水平（通常α = 0.05）

（4）β是期望功效（通常β = 0.8）

（5）Zβ和Zα/2针对给定参数的临界值α和β

固定值：α = 0.05时，Zα/2 = 1.96。β = 0.8时，Zβ = 0.84。

【注册流程改版例子】具体计算过程：

两个版本权重相等的情况

这里使用合并估计量作为方差。

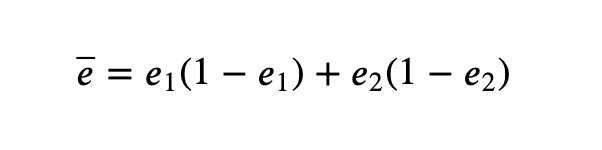
如果我们不假设两个转换率的方差相等，则公式会略有不同，后边给出

代入公式，得到最终的样本的公式：

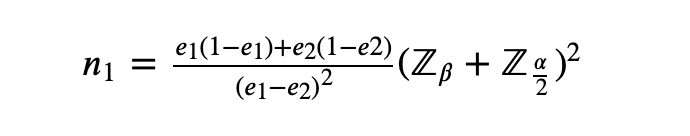
我们来真实计算一下：

1、注册转换率e1为50%，e2为60%

2、假设最小标准值为0.8的期望功效

3、显著性水平α为0.05

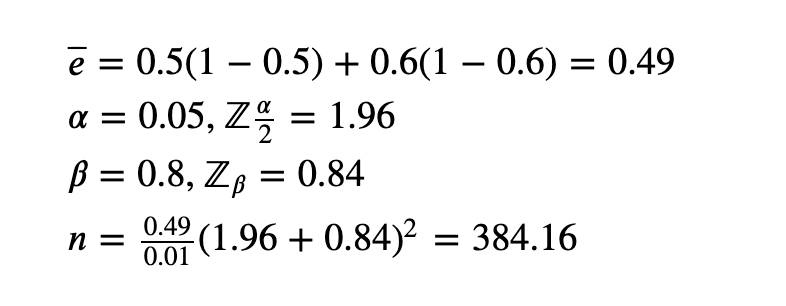
因此。每组（对照组和实验组）的最小样本量为385。

两个版本的注册转换率权重不等的情况

这种情况下，第一步，假设各组大小相等，计算总样本量；然后，可以根据两组实际比率k来调整此总样本量大小N，而修改后的总样本大小N '，可以通过下面公式来计算：

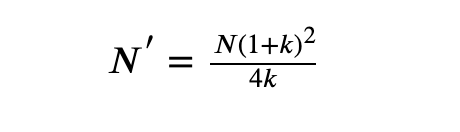
以上两组中，每个样本的样本大小分别为 N '/（1 + k）和 kN '/（1 + k）。

小结

假定两组的总体方差相等，在方差的计算方式上有区别，这类公式不推荐，因为该假设在AB实验应用中并不常见。

4、方法二：使用假设性检验

适用范围

• 假设性检验本身可以对单个总体参数或者两个总体参数进行。

• 假设的内容可以是双侧检验。比如参数是否等于某个值，还可以参数是否大于或者小于某个值。

具体检测和推算

原假设H0：μ1=μ2

备择假设H1：μ1≠μ2

构造统计量

条件：两个样本间，相互独立，且样本量大。

我们实际进行两总体均值差是否为0的双侧检验

实际计算中，总体方差可以用样本方差代替，原假设的背景下u1 - u2 = 0，所以计算统计量z，所需要的数据都可以依据样本得到。

计算原理

下图是概率密度曲线：

1、黄色是AA实验的均值差的分布，蓝色是AB实验（以指标提升为例）的均值差的分布。

2、两个红箭头分别标示 -1.96*指标标准差 +1.96*指标标准差

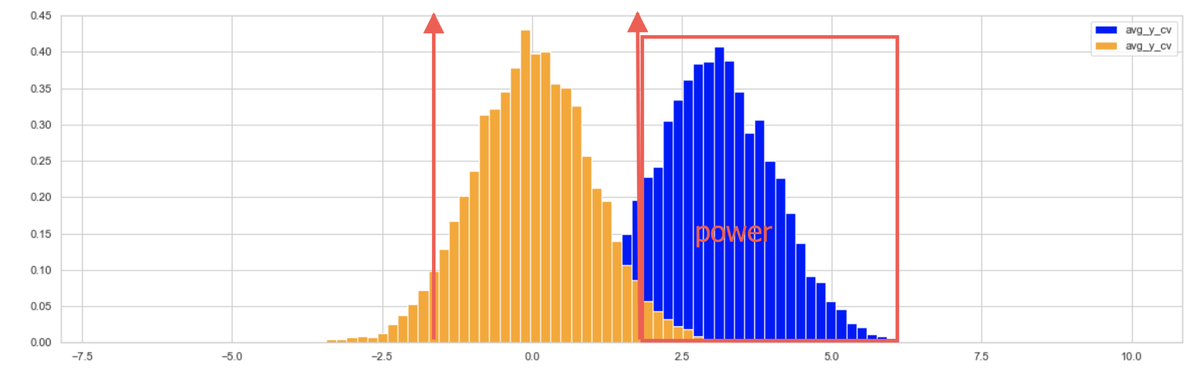
• power 即 蓝色曲线在红色（右）箭头右侧的面积，即显著实验的概率。

• delta是上图 蓝色的中轴位置，即 AB实验（以指标提升为例）的均值差的期望。

其中很多同学可能「power」和「delta」不是很清楚。我们来简单解释一下：

power：统计功效，原假设为假，拒绝愿假设的概率，等于（ 1减第二类错误的概率）。

delta：均值差的期望。

具体推算

根据上面的概率密度曲线和power定义利用标准正态分布的分布函数可以计算power，包含了delta，指标方差，样本量 ；然后根据power公式反推每个版本的样本量。

功效（power）：正确拒绝原假设的概率，记作1-β, 即

power = 1- β（二类错误）

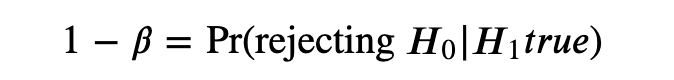
公式：

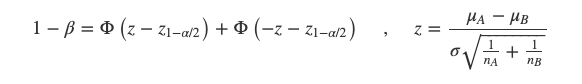
其中：

• σ 是标准差

• Φ是标准正态分布下某个X值对应的概率面积

• α是一类错误概率，叫它alpha

• β是二类错误概率，1-β是统计功效，叫它beta

假设检验的功效受以下三个因素影响：

• 样本量 (n)：其他条件保持不变，样本量越大，功效就越大。

• 显著性水平 (α)： 其他条件保持不变，显著性水平越低，功效就越小。

• 两总体之间的差异：其他条件保持不变，总体参数的真实值和估计值之间的差异越大，功效就越大。也可以说，效应量（effect size）越大，功效就越大。

代入实际计算变量：

power = 1 - norm.cdf( norm.ppf(1 - α / 2) - np.sqrt( sample_per_version * (delta ** 2) / 2 * ( metric_variance ** 2 ) ) )

其中：

• cdf 累积分布函数，是概率密度函数的积分，能完整描述一个实随机变量X的概率分布。

• ppf 分位点函数

• sample_per_version 样本每个版本样本量

• metric_variance 指标方差

• delta 均值的差

根据power，反推出样本量：

公式：

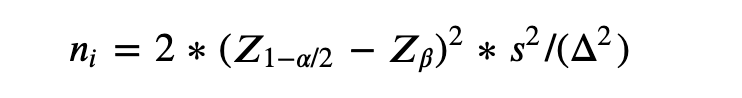
代入实际计算变量：

sample_per_version = 2 * (norm.ppf(1 - α / 2) - norm.ppf(β)) ** 2 * metric_variance / (delta ** 2)

其中：

• ppf 分位点函数

• norm.ppf正态分布的累计分布函数的逆函数，即下分位点。

• alpha 默认5%，其中norm.ppf(1 - α / 2) = 1.96，norm.ppf(β)为映射值。

• metric_variance 指标方差。

• delta 均值的差。

对上述公式做更简单的说，我们只需要知道如下值就可以计算样本量。

（1）希望识别的最小差异，绝对差异（即delta）还是相对差异。

（2）指标方差，方差会根据指标值估算。

（3）alpha 默认是 5%

（4）power 默认是 50%、80%、90%、99%、99.99%

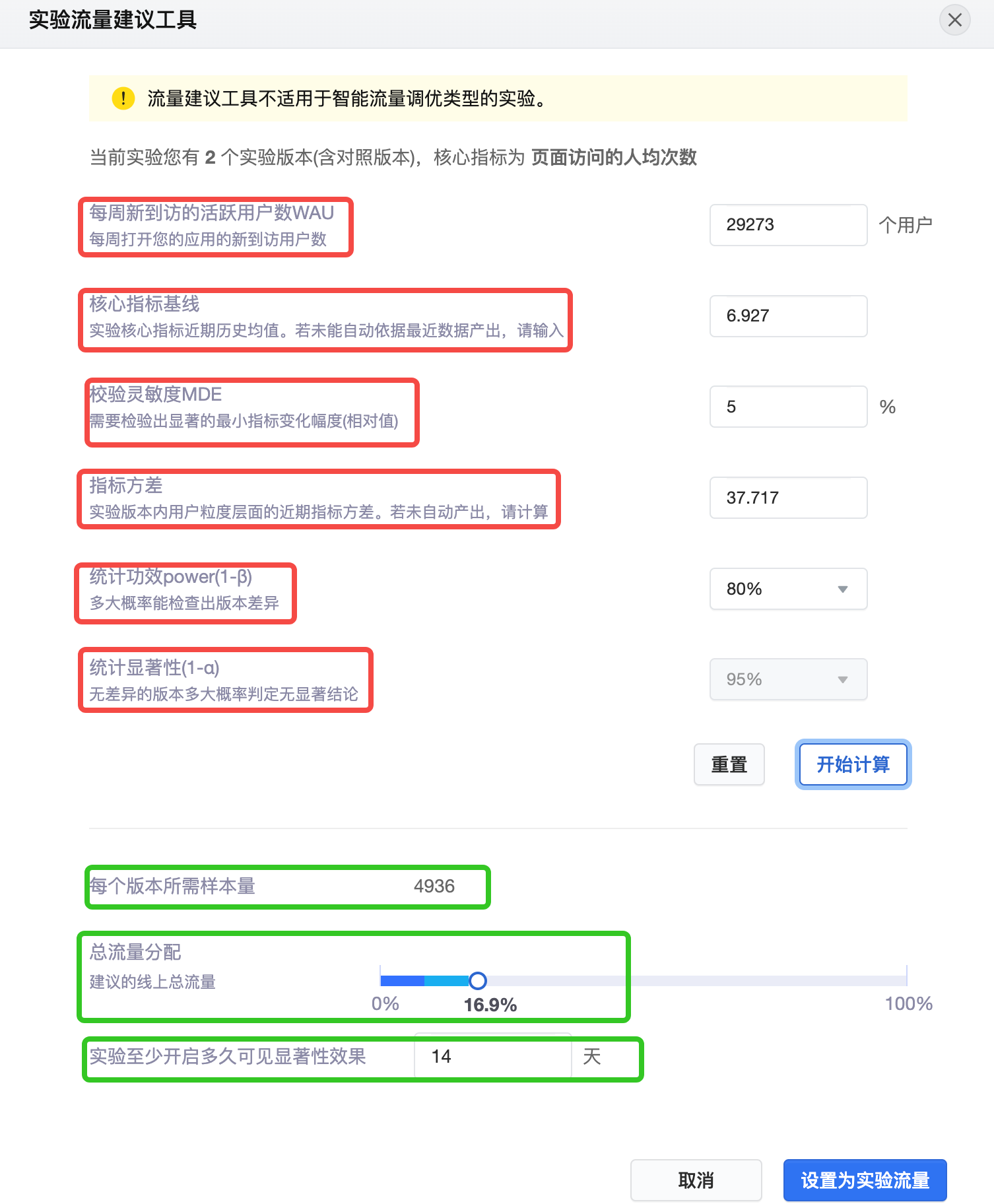
可以使用火山引擎AB测试的流量样本建议工具。

五、最后

其实样本量计算在不同的场景下有不同的计算方式，但是我们针对于主要AB场景下针对可以科学计算置信度的指标，采用的一种计算样本量，从而指导AB实验的流量使用多少和指导实验开启多久。

跳转火山引擎A/B测试DataTester官网了解详情！