【深度学习项目二】卷积神经网络LeNet实现minst数字识别

相关文章：
【深度学习项目一】全连接神经网络实现mnist数字识别
【深度学习项目二】卷积神经网络LeNet实现minst数字识别
【深度学习项目三】ResNet50多分类任务【十二生肖分类】
『深度学习项目四』基于ResNet101人脸特征点检测
项目链接：https://aistudio.baidu.com/aistudio/projectdetail/1928935

1.分类任务介绍

二分类、多分类、多标签

2.图像分类目标和原理

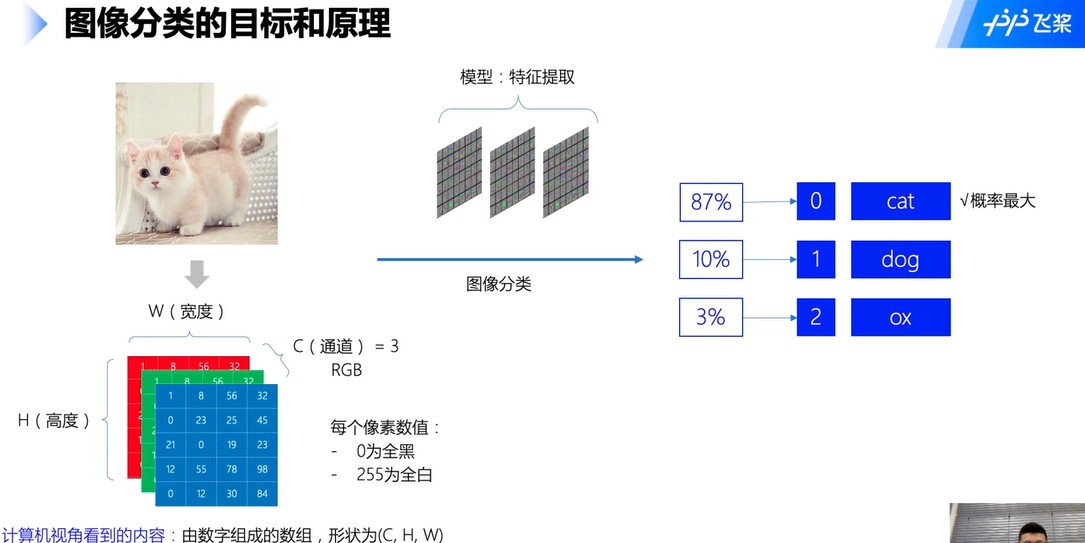
特征会遇到一些干扰：视角变化、形变、遮挡、背景干扰等

神经网络发展过程：

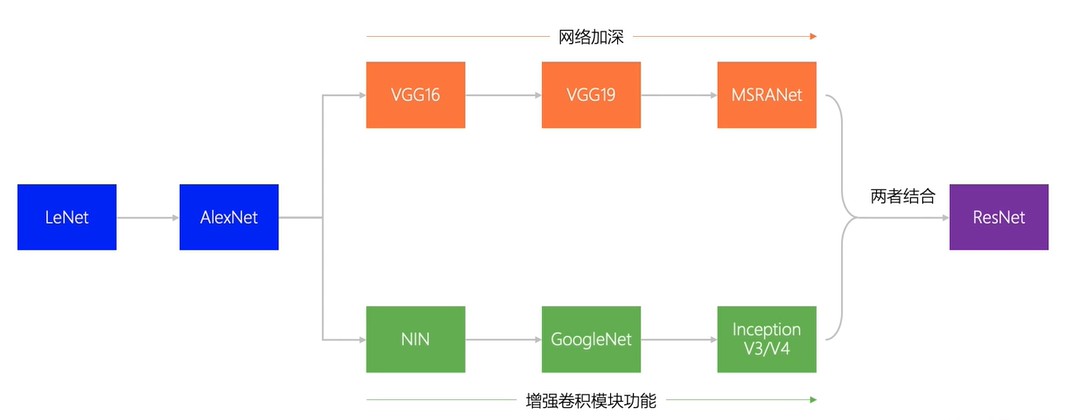
import paddle
import numpy as np
import matplotlib.pyplot as plt

3. 数据准备

继续应用框架中封装好的手写数字识别数据集。

3.1 数据集加载和预处理

# 数据预处理
import paddle.vision.transforms as T
#调用API实现训练时对图像的旋转、形变等，增强样本量，增强模型泛化能力

# 数据预处理
transform = T.Normalize(mean=[127.5], std=[127.5])

# 训练数据集
train_dataset = paddle.vision.datasets.MNIST(mode='train', transform=transform)

# 验证数据集
eval_dataset = paddle.vision.datasets.MNIST(mode='test', transform=transform)

print('训练样本量：{}，测试样本量：{}'.format(len(train_dataset), len(eval_dataset)))

训练样本量：60000，测试样本量：10000

3.2 数据查看

print('图片：')
print(type(train_dataset[0][0]))
print(train_dataset[0][0])
print('标签：')
print(type(train_dataset[0][1]))
print(train_dataset[0][1])

# 可视化展示
plt.figure()
plt.imshow(train_dataset[0][0].reshape([28,28]), cmap=plt.cm.binary)
plt.show()

4 模型选择和开发

选用LeNet-5网络结构。

LeNet-5模型源于论文“LeCun Y, Bottou L, Bengio Y, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278-2324.”，

论文地址：https://ieeexplore.ieee.org/document/726791

4.1 网络结构定义

每个阶段用到的Layer-网络结构依次是：卷积层-池化层-卷积层-池化层-全连接层

4.2卷积操作

4.2.1 单通道卷积

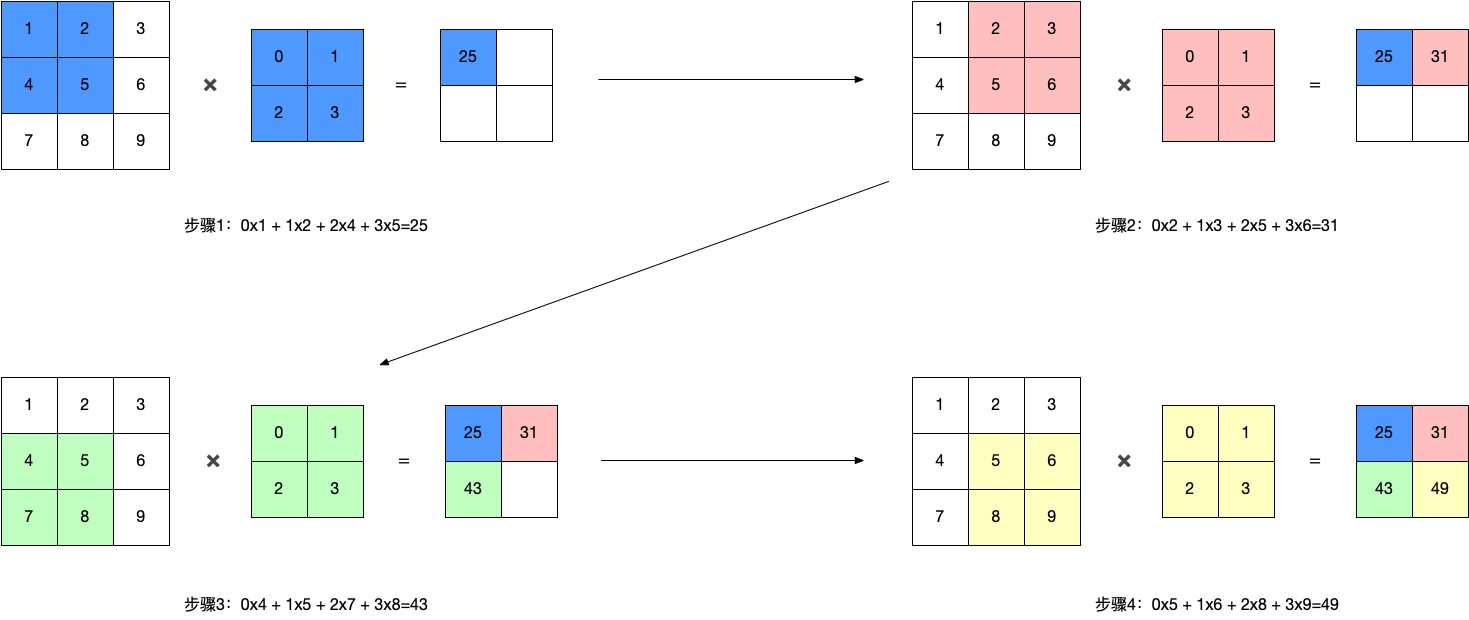
输入单通道图像3x3和2x2卷积核相乘，2x2卷积核的值是通过训练学习的

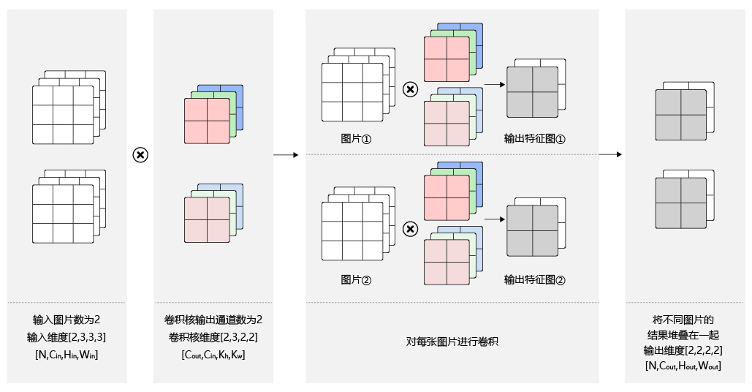
4.2.2 多通道卷积

4.2.3 多通道输出

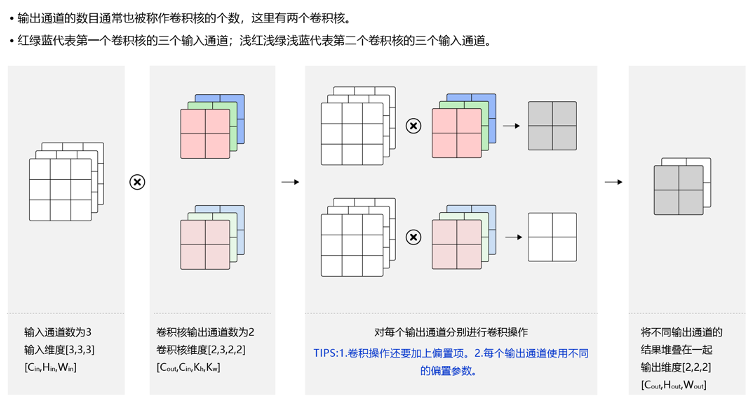
4.2.4 Batch

[N, C, H, W]

卷积核信息不变，卷积操作会多一定的倍数（和样本数有关）。

4.3 池化层

（算力有限才做的）
池化是使用某一位置的相邻输出的总体统计特征代替网络在该位置的输出，其好处是当输入数据做出少量平移时，经过池化函数后的大多数输出还能保持不变。
比如：当识别一张图像是否是人脸时，我们需要知道人脸左边有一只眼睛，右边也有一只眼睛，而不需要知道眼睛的精确位置，这时候通过池化某一片区域的像素点来得到总体统计特征会显得很有用。由于池化之后特征图会变得更小，如果后面连接的是全连接层，能有效的减小神经元的个数，节省存储空间并提高计算效率。

4.3.1池化的作用

池化层是特征选择和信息过滤的过程，过程中会损失一部分信息，但是会同时会减少参数和计算量，在模型效果和计算性能之间寻找平衡，随着运算速度的不断提高，慢慢可能会有一些设计上的变化，现在有些网络已经开始少用或者不用池化层。

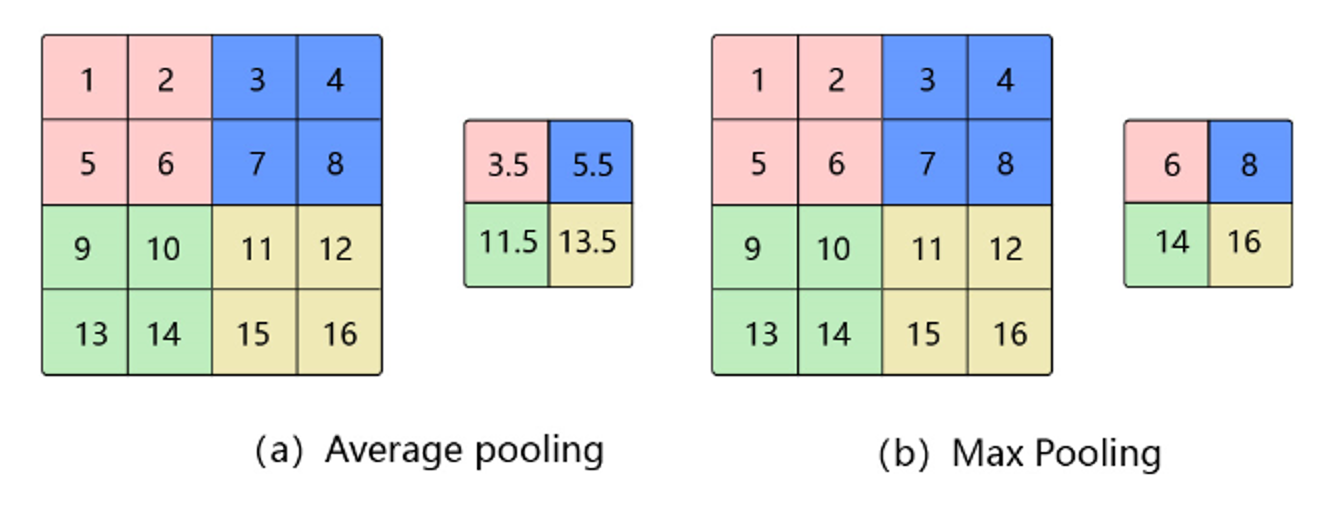
4.3.2 Avg Pooling 平均池化

对邻域内特征点求平均

• 优缺点：能很好的保留背景，但容易使得图片变模糊
• 正向传播：邻域内取平均
• 反向传播：特征值根据领域大小被平均，然后传给每个索引位置

4.3.3 Max Pooling 最大池化

对邻域内特征点取最大，更好保存特征

• 优缺点：能很好的保留一些关键的纹理特征，现在更多的再使用Max Pooling而很少用Avg Pooling
• 正向传播：取邻域内最大，并记住最大值的索引位置，以方便反向传播
• 反向传播：将特征值填充到正向传播中，值最大的索引位置，其他位置补0

4.3.4公式

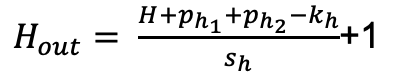
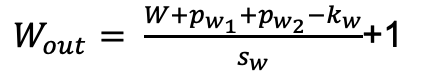
4.4. Padding

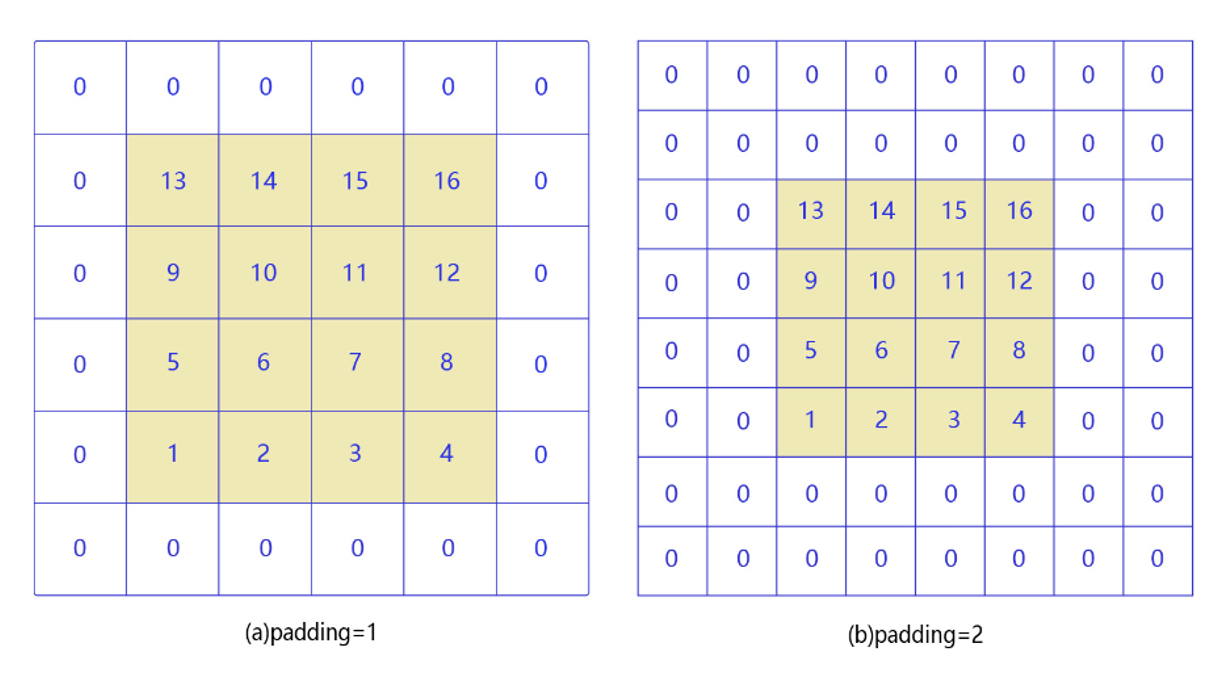
角落边缘的像素，只被一个过滤器输出所使用，因为它位于这个3×3的区域的一角。但如果是在中间的像素点，就会有许多3×3的区域与之重叠。
所以那些在角落或者边缘区域的像素点在输出中采用较少，意味着你丢掉了图像边缘位置的许多信息。

• 解决办法就是填充操作，在原图像外围以0进行填充，在不影响特征提取的同时，增加了对边缘信息的特征提取。

• 另外一个好处是，我们在做卷积操作时，每经过一次卷积我们的输入图像大小就会变小，最后经过多次卷积可能我们的图像会变得特别小，我们不希望图像变小的话就可以通过填充操作。

4.5. 激活函数

参考论文：https://arxiv.org/pdf/1811.03378.pdf

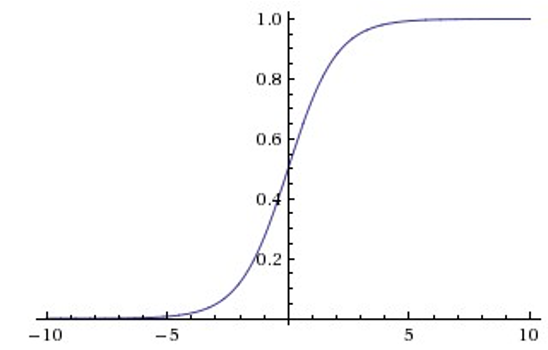
4.5.1 Sigmoid

4.5.2 Tanh

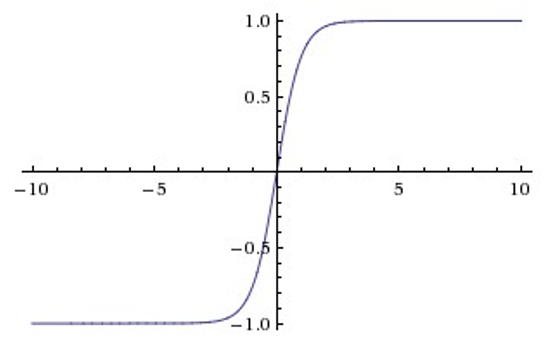
Sigmoid和Tanh激活函数有共同的缺点：即在z很大或很小时，梯度几乎为零，因此使用梯度下降优化算法更新网络很慢。

4.5.3 ReLU

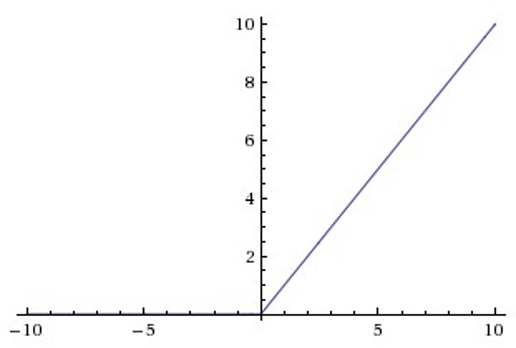
Relu目前是选用比较多的激活函数，但是也存在一些缺点，在z小于0时，斜率即导数为0。
为了解决这个问题，后来也提出来了Leaky Relu激活函数，不过目前使用的不是特别多。

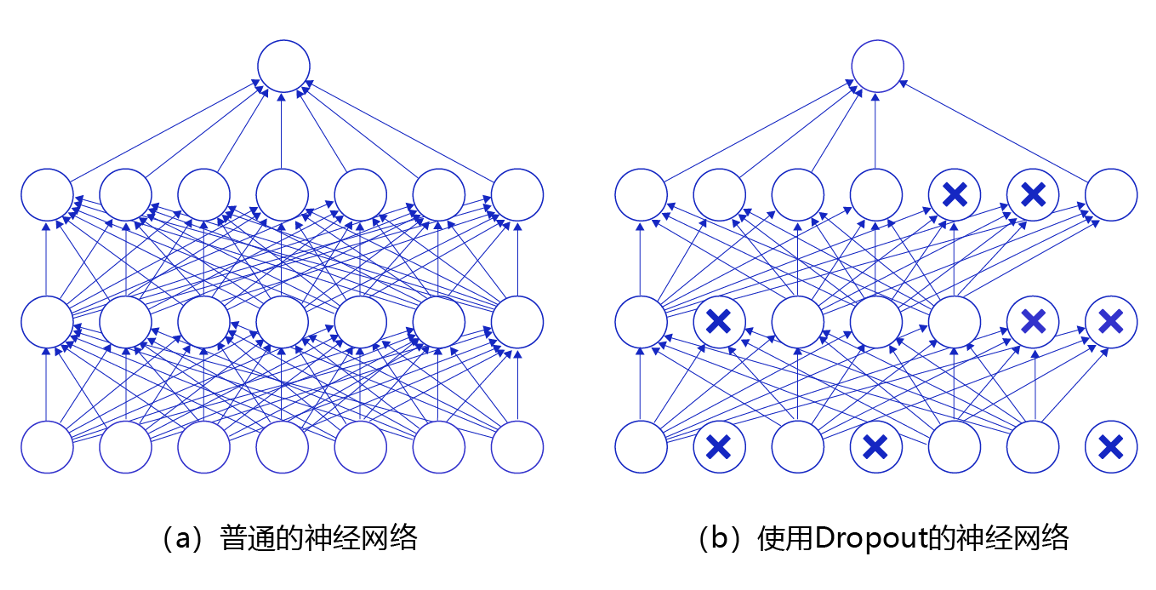
4.6. Dropout

论文：https://jmlr.org/papers/volume15/srivastava14a/srivastava14a.pdf

当一个复杂的前馈神经网络被训练在小的数据集时，容易造成过拟合。为了防止过拟合，可以通过随机丢弃部分特征节点的方式来减少这个问题发生。

5 网络结构代码实现

5.1 网络结构代码实现1

import paddle.nn as nn

network = nn.Sequential(
    nn.Conv2D(in_channels=1, out_channels=6, kernel_size=5, stride=1, padding=0),  # C1 卷积层
    #nn.Conv2D(in_channels=1, out_channels=6, 卷积核kernel_size=(5,6), 步长stride=1, padding=0),
    nn.Tanh(),
    nn.AvgPool2D(kernel_size=2, stride=2),  # S2 平局池化层
    nn.Sigmoid(),   # Sigmoid激活函数；
    #池化不会改变通道数
    nn.Conv2D(in_channels=6, out_channels=16, kernel_size=5, stride=1, padding=0),  # C3 卷积层
    nn.Tanh(),
    nn.AvgPool2D(kernel_size=2, stride=2),  # S4 平均池化层
    nn.Sigmoid(),  # Sigmoid激活函数
    nn.Conv2D(in_channels=16, out_channels=120, kernel_size=5, stride=1, padding=0), # C5 卷积层
    nn.Tanh(),
    nn.Flatten(),#拉平，将原来二维变成一维
    nn.Linear(in_features=120, out_features=84), # F6 全连接层
    nn.Tanh(),
    nn.Linear(in_features=84, out_features=10) # OUTPUT 全连接层
)

模型可视化

paddle.summary(network, (1, 1, 32, 32))

Layer (type)       Input Shape          Output Shape         Param #
===========================================================================
   Conv2D-1       [[1, 1, 32, 32]]      [1, 6, 28, 28]          156
    Tanh-1        [[1, 6, 28, 28]]      [1, 6, 28, 28]           0
  AvgPool2D-1     [[1, 6, 28, 28]]      [1, 6, 14, 14]           0
   Sigmoid-1      [[1, 6, 14, 14]]      [1, 6, 14, 14]           0
   Conv2D-2       [[1, 6, 14, 14]]     [1, 16, 10, 10]         2,416
    Tanh-2       [[1, 16, 10, 10]]     [1, 16, 10, 10]           0
  AvgPool2D-2    [[1, 16, 10, 10]]      [1, 16, 5, 5]            0
   Sigmoid-2      [[1, 16, 5, 5]]       [1, 16, 5, 5]            0
   Conv2D-3       [[1, 16, 5, 5]]       [1, 120, 1, 1]        48,120
    Tanh-3        [[1, 120, 1, 1]]      [1, 120, 1, 1]           0
   Flatten-1      [[1, 120, 1, 1]]         [1, 120]              0
   Linear-1          [[1, 120]]            [1, 84]            10,164
    Tanh-4           [[1, 84]]             [1, 84]               0
   Linear-2          [[1, 84]]             [1, 10]              850
===========================================================================
Total params: 61,706
Trainable params: 61,706
Non-trainable params: 0
---------------------------------------------------------------------------
Input size (MB): 0.00
Forward/backward pass size (MB): 0.12
Params size (MB): 0.24
Estimated Total Size (MB): 0.36
---------------------------------------------------------------------------

{'total_params': 61706, 'trainable_params': 61706}

5.2网络结构代码实现2

用Sequential写法。

import paddle.nn as nn

network_2 = nn.Sequential(
    nn.Conv2D(in_channels=1, out_channels=6, kernel_size=3, stride=1, padding=1),#这里改变了卷积核大小以及加了padding
    nn.ReLU(),
    nn.MaxPool2D(kernel_size=2, stride=2),
    nn.Conv2D(in_channels=6, out_channels=16, kernel_size=5, stride=1, padding=0),
    nn.ReLU(),
    nn.MaxPool2D(kernel_size=2, stride=2),
    nn.Flatten(),
    nn.Linear(in_features=400, out_features=120),  # 400 = 5x5x16，输入形状为32x32， 输入形状为28x28时调整为256
    nn.Linear(in_features=120, out_features=84),
    nn.Linear(in_features=84, out_features=10)
)

5.3 网络结构代码实现3【推荐比较灵活】

模型结构和【网络结构代码实现2】一致，用Sub Class写法。

class LeNet(nn.Layer):
    """
    继承paddle.nn.Layer定义网络结构
    """

    def __init__(self, num_classes=10):
        """
        初始化函数
        """
        super(LeNet, self).__init__()

        self.features = nn.Sequential(
            nn.Conv2D(in_channels=1, out_channels=6, kernel_size=3, stride=1, padding=1),  # 第一层卷积
            nn.ReLU(), # 激活函数
            nn.MaxPool2D(kernel_size=2, stride=2),  # 最大池化，下采样
            nn.Conv2D(in_channels=6, out_channels=16, kernel_size=5, stride=1, padding=0), # 第二层卷积
            nn.ReLU(), # 激活函数
            nn.MaxPool2D(kernel_size=2, stride=2) # 最大池化，下采样
        )

        self.fc = nn.Sequential(
            nn.Linear(400, 120),  # 全连接
            nn.Linear(120, 84),   # 全连接
            nn.Linear(84, num_classes) # 输出层
        )

    def forward(self, inputs):
        """
        前向计算
        """
        y = self.features(inputs)
        y = paddle.flatten(y, 1) #拉伸成一维
        out = self.fc(y)

        return out

network_3 = LeNet()

5.4网络结构代码实现4

直接应用高层API中封装好的LeNet网络接口。

network_4 = paddle.vision.models.LeNet(num_classes=10)

6.模型训练和优化

模型配置

• 优化器：SGD
• 损失函数：交叉熵（cross entropy）
• 评估指标：Accuracy

fit(train_data=None, eval_data=None, batch_size=1, epochs=1, eval_freq=1, log_freq=10, save_dir=None, save_freq=1, verbose=2, drop_last=False, shuffle=True, num_workers=0, callbacks=None)
训练模型。当 eval_data 给定时，会在 eval_freq 个 epoch 后进行一次评估。

参数：
train_data (Dataset|DataLoader) - 一个可迭代的数据源，推荐给定一个 paddle paddle.io.Dataset 或 paddle.io.Dataloader 的实例。默认值：None。

eval_data (Dataset|DataLoader) - 一个可迭代的数据源，推荐给定一个 paddle paddle.io.Dataset 或 paddle.io.Dataloader 的实例。当给定时，会在每个 epoch 后都会进行评估。默认值：None。

batch_size (int) - 训练数据或评估数据的批大小，当 train_data 或 eval_data 为 DataLoader 的实例时，该参数会被忽略。默认值：1。

epochs (int) - 训练的轮数。默认值：1。

eval_freq (int) - 评估的频率，多少个 epoch 评估一次。默认值：1。

log_freq (int) - 日志打印的频率，多少个 step 打印一次日志。默认值：1。

save_dir (str|None) - 保存模型的文件夹，如果不设定，将不保存模型。默认值：None。

save_freq (int) - 保存模型的频率，多少个 epoch 保存一次模型。默认值：1。

verbose (int) - 可视化的模型，必须为0，1，2。当设定为0时，不打印日志，设定为1时，使用进度条的方式打印日志，设定为2时，一行一行地打印日志。默认值：2。

drop_last (bool) - 是否丢弃训练数据中最后几个不足设定的批次大小的数据。默认值：False。

shuffle (bool) - 是否对训练数据进行洗牌。当 train_data 为 DataLoader 的实例时，该参数会被忽略。默认值：True。

num_workers (int) - 启动子进程用于读取数据的数量。当 train_data 和 eval_data 都为 DataLoader 的实例时，该参数会被忽略。默认值：0。

callbacks (Callback|list[Callback]|None) - Callback 的一个实例或实例列表。该参数不给定时，默认会插入 ProgBarLogger 和 ModelCheckpoint 这两个实例。默认值：None。

# 模型封装
model = paddle.Model(network_4)

# 模型配置
model.prepare(paddle.optimizer.Adam(learning_rate=0.001, parameters=model.parameters()), # 优化器
              paddle.nn.CrossEntropyLoss(), # 损失函数
              paddle.metric.Accuracy()) # 评估指标

callback = paddle.callbacks.VisualDL(log_dir='visualdl_log_dir_LeNet学习率0.001')
# 启动全流程训练
model.fit(train_dataset,  # 训练数据集
          eval_dataset,   # 评估数据集
          epochs=5,       # 训练轮次
          batch_size=64,  # 单次计算数据样本量
          verbose=1,
          callbacks=callback
          )      # 日志展示形式

The loss value printed in the log is the current step, and the metric is the average value of previous step.
Epoch 1/5
step 938/938 [==============================] - loss: 0.0221 - acc: 0.9867 - 21ms/step
Eval begin...
The loss value printed in the log is the current batch, and the metric is the average value of previous step.
step 157/157 [==============================] - loss: 0.0037 - acc: 0.9849 - 9ms/step
Eval samples: 10000
Epoch 2/5
step 938/938 [==============================] - loss: 0.0251 - acc: 0.9893 - 21ms/step
Eval begin...
The loss value printed in the log is the current batch, and the metric is the average value of previous step.
step 157/157 [==============================] - loss: 1.8192e-04 - acc: 0.9837 - 8ms/step
Eval samples: 10000
Epoch 3/5
step 938/938 [==============================] - loss: 0.0029 - acc: 0.9903 - 21ms/step
Eval begin...
The loss value printed in the log is the current batch, and the metric is the average value of previous step.
step 157/157 [==============================] - loss: 6.0831e-04 - acc: 0.9826 - 9ms/step
Eval samples: 10000
Epoch 4/5
step 938/938 [==============================] - loss: 4.9427e-04 - acc: 0.9916 - 21ms/step
Eval begin...
The loss value printed in the log is the current batch, and the metric is the average value of previous step.
step 157/157 [==============================] - loss: 5.9639e-04 - acc: 0.9809 - 8ms/step
Eval samples: 10000
Epoch 5/5
step 938/938 [==============================] - loss: 0.0323 - acc: 0.9914 - 21ms/step
Eval begin...
The loss value printed in the log is the current batch, and the metric is the average value of previous step.
step 157/157 [==============================] - loss: 3.1420e-04 - acc: 0.9834 - 8ms/step

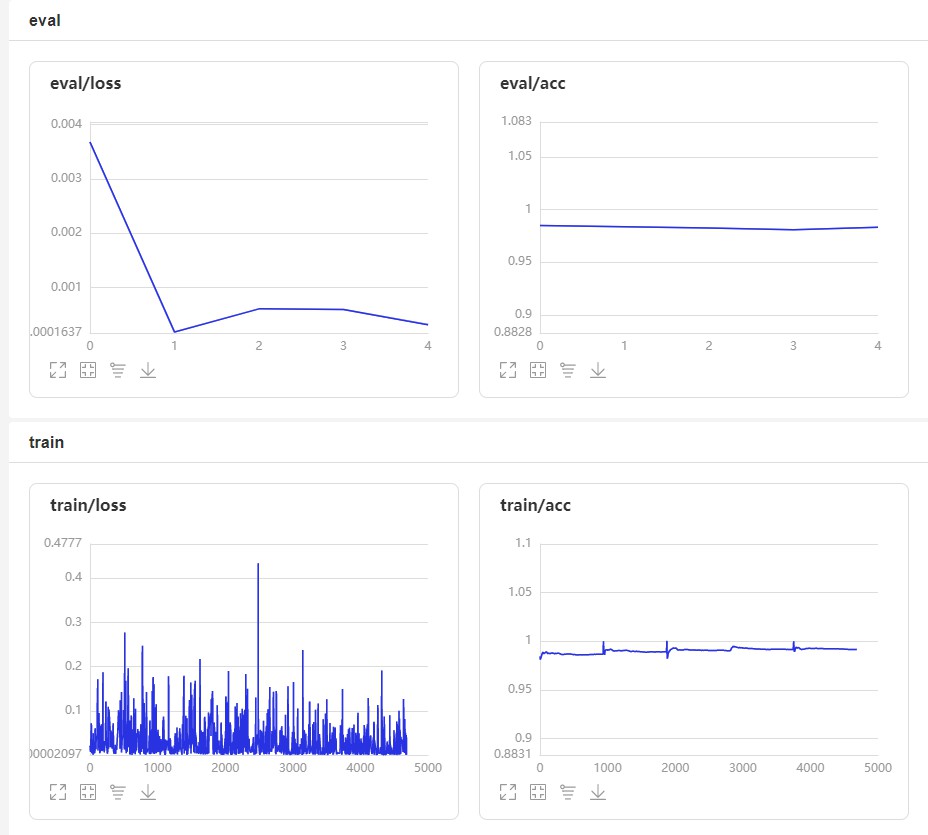
6.1可视化训练结果

7 模型评估

7.1 模型评估

evaluate(eval_data, batch_size=1, log_freq=10, verbose=2, num_workers=0, callbacks=None)
在输入数据上，评估模型的损失函数值和评估指标。

参数：
eval_data (Dataset|DataLoader) - 一个可迭代的数据源，推荐给定一个 paddle paddle.io.Dataset 或 paddle.io.Dataloader 的实例。默认值：None。

batch_size (int) - 训练数据或评估数据的批大小，当 eval_data 为 DataLoader 的实例时，该参数会被忽略。默认值：1。

log_freq (int) - 日志打印的频率，多少个 step 打印一次日志。默认值：1。

verbose (int) - 可视化的模型，必须为0，1，2。当设定为0时，不打印日志，设定为1时，使用进度条的方式打印日志，设定为2时，一行一行地打印日志。默认值：2。

num_workers (int) - 启动子进程用于读取数据的数量。当 eval_data 为 DataLoader 的实例时，该参数会被忽略。默认值：True。

callbacks (Callback|list[Callback]|None) - Callback 的一个实例或实例列表。该参数不给定时，默认会插入 ProgBarLogger 和 ModelCheckpoint 这两个实例。默认值：None。

返回：dict, key是 prepare 时Metric的的名称，value是该Metric的值。

result = model.evaluate(eval_dataset, verbose=1)

print(result)

Eval begin...
The loss value printed in the log is the current batch, and the metric is the average value of previous step.
step 10000/10000 [==============================] - loss: 6.9142e-06 - acc: 0.9846 - 3ms/step
Eval samples: 10000
{'loss': [6.914163e-06], 'acc': 0.9846}

7.2 模型预测

7.2.1 批量预测

使用model.predict接口来完成对大量数据集的批量预测。

# 进行预测操作
result = model.predict(eval_dataset)

# 定义画图方法
def show_img(img, predict):
    plt.figure()
    plt.title('predict: {}'.format(predict))
    plt.imshow(img.reshape([28, 28]), cmap=plt.cm.binary)
    plt.show()

# 抽样展示
indexs = [5, 20, 48, 210]

for idx in indexs:
    show_img(eval_dataset[idx][0], np.argmax(result[0][idx]))

8 部署上线

8.1 保存模型

model.save('finetuning/mnist')

8.2 继续调优训练

from paddle.static import InputSpec

network = paddle.vision.models.LeNet(num_classes=10)
# 模型封装，为了后面保存预测模型，这里传入了inputs参数
model_2 = paddle.Model(network, inputs=[InputSpec(shape=[-1, 1, 28, 28], dtype='float32', name='image')])

# 加载之前保存的阶段训练模型
model_2.load('finetuning/mnist')

# 模型配置
model_2.prepare(paddle.optimizer.Adam(learning_rate=0.0001, parameters=network.parameters()),  # 优化器
                paddle.nn.CrossEntropyLoss(), # 损失函数
                paddle.metric.Accuracy()) # 评估函数
callback = paddle.callbacks.VisualDL(log_dir='visualdl_log_dir_LeNet学习率0.0001')
# 模型全流程训练
model_2.fit(train_dataset,  # 训练数据集
            eval_dataset,   # 评估数据集
            epochs=2,       # 训练轮次
            batch_size=64,  # 单次计算数据样本量
            verbose=1,        # 日志展示形式
            callbacks=callback)       #可视化

The loss value printed in the log is the current step, and the metric is the average value of previous step.
Epoch 1/2
step 938/938 [==============================] - loss: 0.0038 - acc: 0.9934 - 21ms/step
Eval begin...
The loss value printed in the log is the current batch, and the metric is the average value of previous step.
step 157/157 [==============================] - loss: 5.2845e-04 - acc: 0.9871 - 9ms/step
Eval samples: 10000
Epoch 2/2
step 938/938 [==============================] - loss: 9.8578e-04 - acc: 0.9952 - 21ms/step           0.0021 - acc:
Eval begin...
The loss value printed in the log is the current batch, and the metric is the average value of previous step.
step 157/157 [==============================] - loss: 4.6717e-04 - acc: 0.9873 - 8ms/step
Eval samples: 10000

效果图

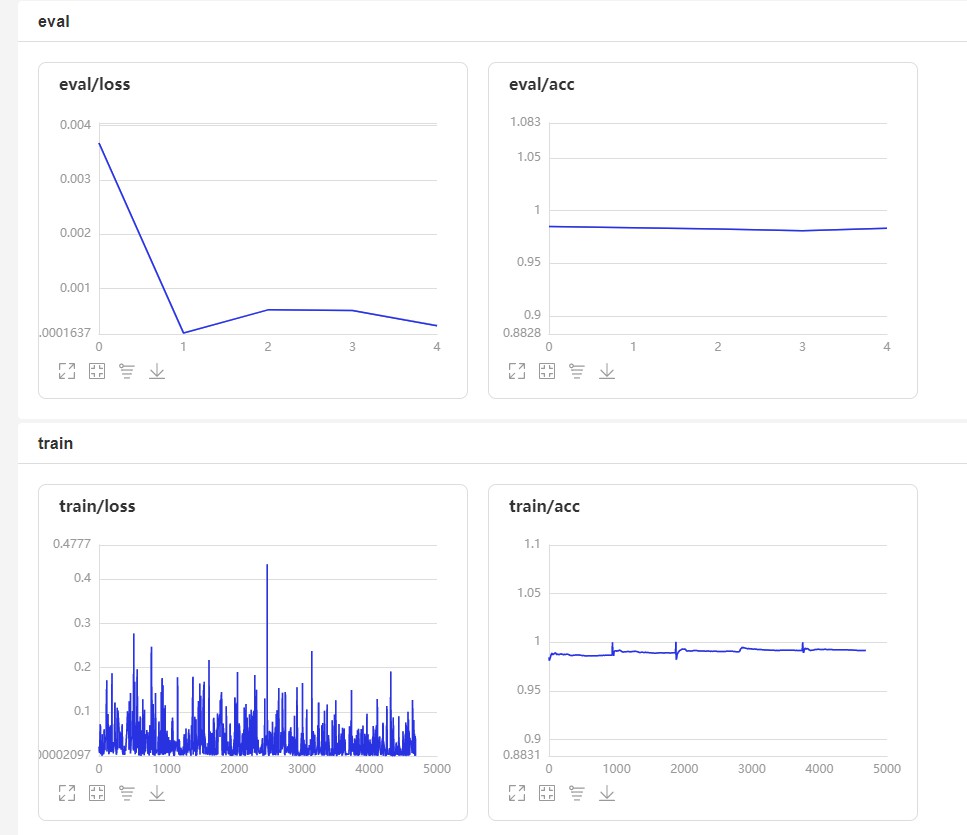
8.3 保存预测模型

# 保存用于后续推理部署的模型
model_2.save('infer/mnist', training=False)

总结

可以看到再采用LeNet卷积网络后数字识别的准确率比项目一中全连接形式准确率提高，精益求精了。

不过这个项目只是单通道的黑白图识别，下面在项目三种我将介绍其余几种热门更加使用的复杂卷积，以及实现彩色图片多分类任务